SpMV矩阵格式自动调优
SpMV的自动调优和矩阵格式和kernal实现都有关系,在这样的调研中,我们主要关注具体的建模和模型训练手段。
1、
Adaptive SpMV/SpMSpV on GPUs for Input Vectors of Varied Sparsity
在机器学习的应用中,不仅仅稀疏矩阵乘密集向量,稀疏矩阵乘稀疏向量也很多。这篇文章同时处理这两个问题,并且根据输入的实际情况,来选择最优的kernal实现。这篇文章的稀疏矩阵,默认采用CSR和CSC格式。
计算模式、线程的分配、线程中间结果的规约策略是kernal实现的三个方面。计算模式包括向量是稀疏的还是密集的,在SpMV中的线程是按照行方向遍历矩阵还是列方向遍历矩阵。线程的分配包括,是将行和列以对齐的方式分配给线程(每个线程固定一行或者一列),还是给每个线程分配相同数量的非零元(优先保证线程的负载均衡)。对于线程的计算方向和非零元分配如下图所示,同一个颜色代表分别到同一个线程的元素:

当每个线程按列处理数据时,每个线程都要更新y中的所有元素,这就有两种更新方法,一种是通过原子操作对显存上的y直接原子加(atom),还有一种是将每个线程中对每一行执行的中间结果按照<行号,值>的方式暂时放在显存中,然后按照行排序,将每一个线程同一行的中间结果排在一起,然后再用一个kernal来reduce by key,这种方式叫sort-based,可以不用同步的方式来规约结果。
这三种执行策略可以产生一个三层的决策树:

这里的1、2、3分别是用来做选择的机器学期模型,将输入矩阵和向量的特征分别输入这三个模型就能分别在三层中做选择。这些特征不赘述了,主要是一些矩阵和向量的形状、稀疏的程度、非零元的分布等信息,不同模型的输入是不一样的:

用的模型是decision tree,SVM,random forest,gradient tree boosting。
2、
Adaptive Optimization of Sparse Matrix-Vector Multiplication on Emerging Many-Core Architectures
在SpMV中,根据矩阵特征选格式。特征就是矩阵的形状和非零元分布的信息:

为了屏蔽数据结构之外因素的影响,文章将每个数据结构的SpMV实现调到了最优。文章选择以下模型做了测试:decision tree based model (DTC),Gaussian naive bayes (GNB),multilayer perception (MLP),soft voting/majority rule Classification (VC),k-Nearest Neighbor (KNC, k=1),logistic regression (LR),random forests classification (RFC)。
3、
Automatic Selection of Sparse Matrix Representation on GPUs
这篇文章认为已有的矩阵格式设计本质就是分块,已有的autotunning的本质就是调blocksize。这篇文章主要是根据不同的输入矩阵特征,从cuSPARSE、CUSP两个库中,选择ELL、CSR、COO、HYB的SpMV实现。是一个选库、选实现的工作。
使用的特征是如下图:

这个工作在特征选取很有意思,除了每一行的非零元分布(nnz_tot、nnz_frac)之外,每一行连续非零元的数量和大小也被纳入考虑(一行中连续非零元的数量,长度,nnzb*)。
最终使用的模型是最为简单的决策树。
4、
Auto-Tuning Strategies for Parallelizing Sparse Matrix-Vector (SpMV) Multiplication on Multi- and Many-Core Processors
针对AMD APU的CSR格式的自动调优,但是整体语境和CUDA没有什么区别。这篇文章的优点就是在于,它同时调优了分块策略和每个并行策略(kernal实现策略)。这篇文章的主要目的就是将负载类似的矩阵行分到同一个桶(bin),保证每一个桶内部的矩阵行的非零元数量差不多。然后为每一个桶准备一个kernal,每个kernal采用不同的实现和并行策略。综上,这个工作是将相同模式的行放在一起处理,这样子方便对特定模式行执行统一的优化。如下图所示:
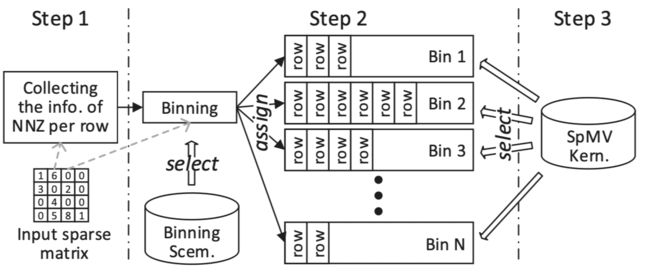
因为出现了桶、kernal与行号的对应关系,所以相比CSR需要加一个新的索引。
行的分桶。将每个行的非零元记录出来,然后根据非零元的数量分到对应的桶里面,是核心目的。但是,在实践过程中,为了减少预处理的时间,可以增加调度的粒度,即将多个相邻的行划分为一个“虚行”,根据虚行内部的平均行非零元大小来将虚行分配到对应的桶。其中“虚行”所包含的实际行的数量是一个可调的参数。
不同的kernal。每个桶都需要根据桶中行非零元的数量选择合适的kernal,这篇文章根据行与线程分配的对应关系给出了三种候选的内核:1)bin中的一行分配一个线程,2)bin中的一行分配多个线程,但是线程数量少于一个线程块的线程数量,一个线程块负责多行,3)一行分配一个线程块。因为不喜欢全局同步,所以这篇文章拒绝让多个线程块处理一行。具体选择哪一种kernal也是一个可调参数。
这篇文章分阶段地找出两个参数,首先跟根据矩阵的形状和非零元分布找出最合适的分桶调度粒度,然后根据形状、非零元分布、调度粒度以及桶中行平均非零元数量找出最合适的kernal。
矩阵属性的选择如下图,使用的模型是C5.0 data mining tool。

自动化矩阵分解、格式选择、kernal选择的鼻祖:
clSpMV: A Cross-Platform OpenCL SpMV Framework on GPUs
将矩阵分解为一系列的子矩阵,然后每个子矩阵选择一个最优的格式,最后每个格式选择最优的实现,这是矩阵自动调优的理想流程。但是搜索空间实在是太大了。尤其是矩阵分解的策略,带来的搜索空间是巨大的,因为几乎每个非零元都可以属于不同的子矩阵。这是clSpMV解决的第一个问题;第二个问题是如果不使用预运行的方式搜索一个特定矩阵的最优格式。clSpMV使用的基于cost model的方式,直接用cost model估计出搜索空间中对应格式的计算时间。clSpMV提供了9种格式70多种实现,包含了对角矩阵(DIA等)、稠密子块矩阵(BCSR等)、一般稀疏矩阵(ELL等)的表示类型。
首先针对第一个问题,本文提出了基于贪心算法的矩阵分解策略,通过对比对角矩阵存储与一般稀疏矩阵表示在矩阵对角线部分的执行时间,绝对对角线是不是稠密的,并且将对角线分解出来用对角格式存储。稠密子块格式也是同理,通过不断改变矩阵分块的大小,对比稠密子块格式相比一般格式的性能是不是更高,从而判断稠密矩阵的格式是不是要在稠密子块中被使用。而一般稀疏矩阵格式就是一种缺省的选择了。所以,文章在确定的优先级下(优先级需要预执行的性能比较来得到,文章中对角线> 稠密块>一般格式),分别将稀疏矩阵分解为最多三个子矩阵,每个子矩阵对应三类格式中的其中一类。当然,三类矩阵中具体使用哪一个格式,需要继续执行比较
针对第二个问题,文章提出了基于统计的cost model。因为矩阵的分解策略已经被剪枝为一个贪心算法,所以cost model的部分只包含了特定矩阵在特定格式下的执行时间,整体的构建方式和一般文章是大同小异的。这篇文章的模型训练工作采样点(比如输入矩阵的大小)非常稀疏,以指数增长。值得一提的是clSpMV的样本是自己生成的,这样子有利于自己决定采样点,降低训练的时间。有了cost model,第一个问题中的性能比较就不需要真正执行了,使用cost model直接判断比较就好了。
除此之外,clSpMV给出了一些很有意义的观点:1)CPU喜欢粗粒度并行,GPU喜欢细粒度并行,2)对矩阵进行分块后,如果每个块都按照稠密矩阵的方式存储,可以利用float4这种大数据类型。3)分块之后,x和y都能更方便用到shared memory。线程块中的一个wrap可以先把需要的数据放到shared memory,其他线程就不需要读全局内存了。
还是用CNN来分类矩阵,但不是仅仅将矩阵压缩一下就喂给模型,而是利用CNN的多个通道类提取矩阵的不同特征:
A New Approach for Sparse Matrix Classification Based on Deep Learning Techniques
将矩阵最优格式选择建模成一个图像分类问题。因为CNN的输入大小是固定的,而一个稀疏矩阵的规模通常会远大于CNN的输入规模,所以原始的稀疏矩阵要进行分块,块矩阵的规模和CNN的输入保持一致,将分块后的每个子矩阵块压缩成CNN输入的一位(等同于图像的一个像素)。
因为将一个矩阵压缩成一个更小的矩阵肯定丢失信息,所以如果能够保留别压缩的每个子矩阵块的某些特征是很有意义的。最终,这篇文章将一个大矩阵压缩成多个与CNN输入大小一致的小矩阵,每个小矩阵都存储子块的一个特征(总非零元数量,行非零元数量平均值,等等),然后将这些小矩阵喂给CNN输入的不同通道。子块的特征包括:

也就说一个大矩阵可以变成一张5个通道图片,最终将“图片”和其对应的最优格式丢给CNN做分类。
7、用SVM分类器来选择最优的矩阵格式:
BestSF: A Sparse Meta-Format for Optimizing SpMV on GPU
相比之前的研究,本文加入了基于块矩阵格式:BCSR。与已有的方式不同,本文采用SVM来执行分类,6个格式,将格式之间两两组合,共15个格式对,每个格式对都对应一个模型,输入是矩阵的特征,输出是性能更高的格式。面对一个矩阵,我们需要在所有的矩阵格式之间进行两两比较,选出胜出最多的一个。因为每两个矩阵之间的性能差距不一样,所以所有的二分类器都有一个权重,两种格式的性能差距越大,权重越大。

上图是所选的矩阵特征,除了标准的行非零元平均值和方差之外,还有平局值和方差的比值,行非零元最大值,行非零元最大值与平均值差值,对角线数量,相邻非零元之间的平均距离(对分块矩阵类型的格式很有用)。
Bridging the Gap between Deep Learning and Sparse Matrix Format Selection
(略)