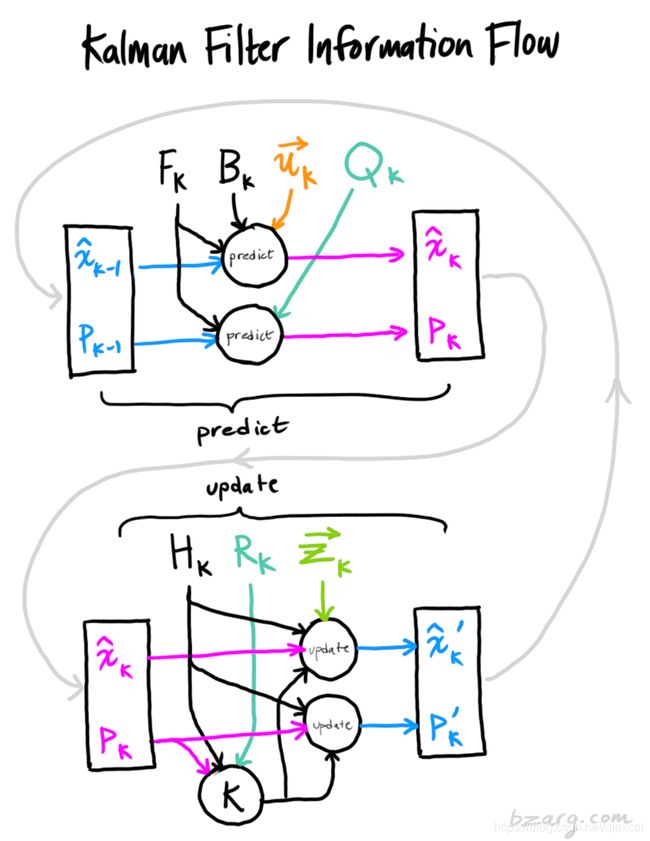
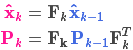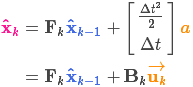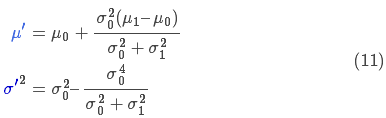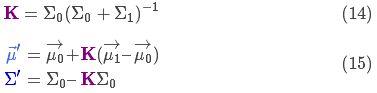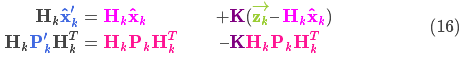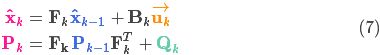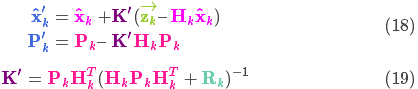讲解卡尔曼滤波附代码讲解

本文很多内容来自https://blog.csdn.net/u010720661/article/details/63253509，笔者只是按照自己的理解转述一下。

代码部分来自：https://www.cnblogs.com/yueyangtze/p/9503835.html

 

一、应用领域

1、存在误差的传感器的值和自己的估计值之间相信谁。比如：一个温度计，误差在2度左右。现在它显示温度为30度，可是你自己根据经验判断当前温度为29度。那么当前真实温度最有可能为多少？

2、两个或多个传感器之间相信谁。比如：两个温度计，误差分别2度和3度。现在一个显示30度，一个显示29度，那么当前真实温度最有可能为多少？

        面对上面两个问题，我们一般选择一个权重值，比如温度计1权重为0.3，温度计2权重为0.7，那么把两个温度计的读数乘以各自的权重再相加得到我们最相信的温度值，这种方法就叫互补滤波。

        这种方法对于权重值的选择很关键，如果选的好，那结果就很好，选的差，结果就不好，而且一旦选好后，就不能改变。那么有没有一种可以自己确定权重值的办法呢？有，那就是卡尔曼滤波，它可以自己迭代权重值，以获得最好的输出值。
二、准备知识

1、高斯分布

     又名正态分布，用以描述随机事件的概率分布。比如硬币的正反面。详情参考这儿：https://blog.csdn.net/zw0pi8g5c1x/article/details/95268724

2、方差、协方差
        两个数的方差就是两个数差值的平方，作为衡量实际问题的数字特征，方差有代表了问题的波动性。

        协方差表示的是两个变量总体误差的期望。如果两个变量的变化趋势一致，也就是说如果两个变量都大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。当两个变量完全一致时，协方差就变成了方差

详情参考这儿：https://www.cnblogs.com/bigmonkey/p/11097322.html
二、正文

1、问题的引出

        现在有一个在树林里到处跑的小机器人，你要为它导航，所以你需要知道它的确切状态。状态包括它的运行速度和位置，写为：

        上式中p表示位置，v表示速度，它们都有方向，都是向量。

        机器人带有速度计和GPS可以测量机器人的速度和位置，可是它们都有误差，速度计误差为0.1m/s，GPS误差为10m。

        机器人上可以测量运动的时间，同时机器人的初始状态是已知的（比如位置为10，速度为5），因此可以根据运动时间、初始速度和初始位置预测出现在的状态（假定机器人匀速运动）。可是树林的路崎岖不平，还有风吹等影响因素。因此我们预测出的机器人状态也是有误差的。

        现在问题来了，当前机器人最有可能的状态是什么？

2、问题的转化及协方差矩阵的引出

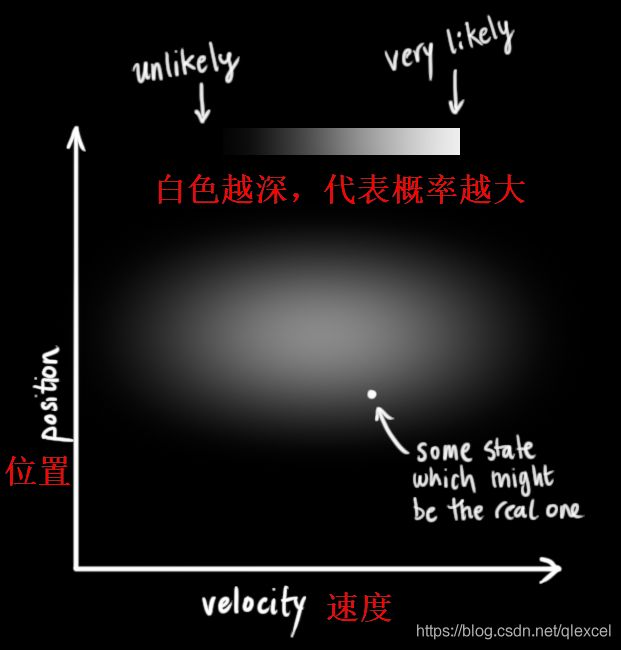
        假如我们预测出机器人位置为30，但是真实的位置会因为道路的崎岖、风等因数影响，因此真实的位置可能在一个区间里，比如[20,40]。机器人的位置是区间中哪个值是随机的，同时机器人的位置在这个区间里的概率也不是均匀分布的，不同位置的概率有大有小，比如在30m这个位置的概率一般比较大一些。同样的道理，真实的速度值也是一个区间。把位置区间和速度区间表示为图形：

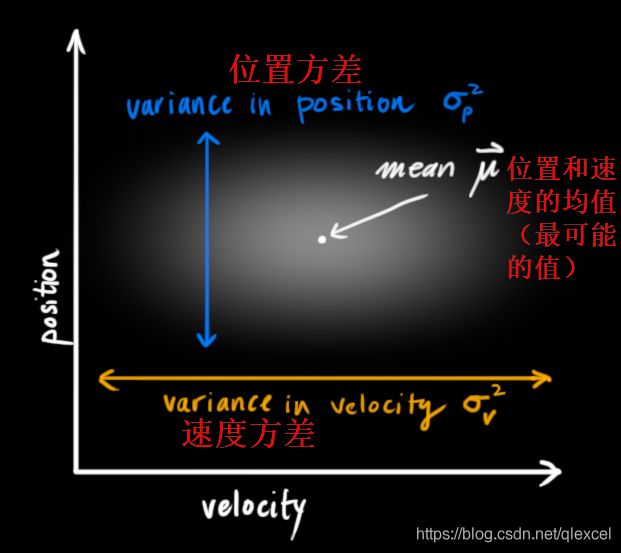
        小车的两个状态变量是随机的，即它们服从高斯分布（正态分布）。因此每个变量都有一个均值μ，表示随机分布的中心（最可能的位置值或速度值），以及方差，表示对于该变量的不确定度（即区间的大小，区间越大，真实值是哪个值就越不好确定）

        从上图可以看出，位置和速度是不相关的，即知道一个变量无法推测出另一个变量的可能值。比如我们固定了一个速度值（在上图中画一条竖线），从上图可以看出，位置值在这个速度值下的变化范围为[a,b]，现在我们增加速度值（竖线往右移动），位置值在这条竖线的变化范围还是[a,b]，位置的变化范围没有变。即速度的变化不会对位置的分布造成影响。

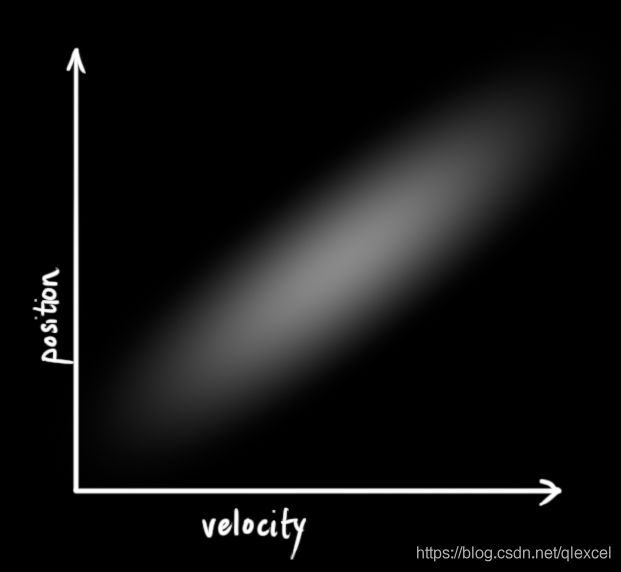
        下面再给出一个关系图：

        从上图中就可以看出来，速度和位置是相关的，即我们可以从一个变量推测出另一个变量的可能值。还是在上图中画一条竖线，从上图可以看出，位置值在这个速度值下的变化范围为[a,b]，现在我们增加速度值（竖线往右移动），位置值在这条竖线上的变化范围就变为[c,d]了，可见速度的变化对位置的分布造成了影响。

        如果一个系统中的几个变量是相关的，那么我们就要好好利用这种相关性来推测出系统最可能的状态。这就是卡尔曼滤波的目的，尽可能地在包含不确定性的测量数据中提取更多信息！

        变量之间的相关性用协方差来表示，如果一个系统中有n个变量我们就用n阶的协方差矩阵来表示。矩阵中的每个元素，表示第i个和第j个状态变量之间的相关度。（协方差矩阵是一个对称矩阵，这意味着可以任意交换 i 和 j）。协方差矩阵通常用“”来表示，其中的元素则表示为“ ”。 

3、使用矩阵来描述问题

        我们所研究的小车系统中仅包含两个变量，因此我们把小车的状态转变为一个2x1的矩阵：

        上式中，是小车状态的均值，即小车最可能的状态，也叫最佳估计。Pk是描述系统中两个变量相关性的协方差矩阵。

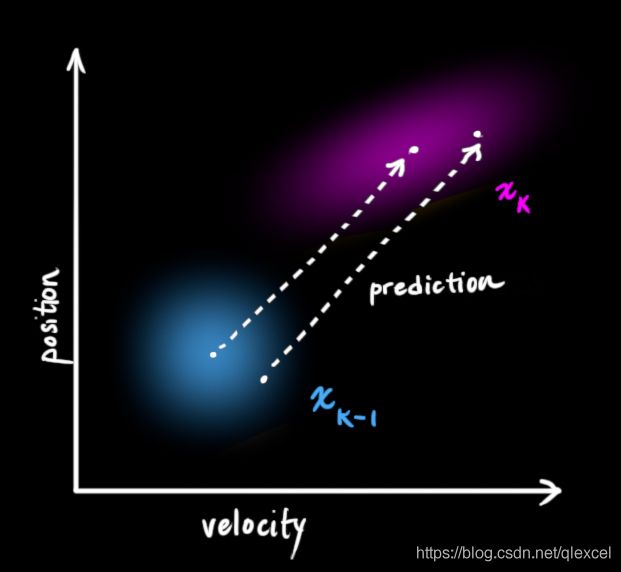
        假设我们现在处于k-1时刻，我们知道系统当前的和Pk，小车在继续运动，现在要预测k时刻的和Pk，表示为下图：

我们可以用矩阵来表示这个预测过程：

        用基本的运动学公式来表示预测的k时刻的位置和速度：

        现在k时刻的已经得到了，那么k时刻的Pk如何得到呢？已知k-1时刻的Pk表示为：

        现在Pk矩阵中的两个变量都已经乘了Fk矩阵，那么Pk的计算公式如何变化呢？直接给出如下计算公式：

        即：如果协方差矩阵中的每个元素都乘以矩阵A，等于矩阵A乘以协方差矩阵再乘以矩阵A的秩。

        因此由k-1时刻的和Pk计算k时刻的和Pk，表达式为：

4、考虑系统自身对状态的干预

        上面的推测过程是假定小车在匀速直线运动的，没有考虑小车是否在加速运动。因此假定小车的加速度等于a，那么运动方程为：

表示为矩阵：

称为控制矩阵，称为控制向量。

5、外部干扰对预测的影响

        前面说了因为路面的崎岖和风等因素会对我们的预测结果造成干扰。

        k-1时刻更新到k时刻后，虽然因为外界干扰，增加了新的不确定性，但是仍然服从高斯分布。因此我们可以说的每个状态变量移动到了一个新的服从高斯分布的区域。我们用协方差改变了来表示外界干扰。因此预测方程变为：

        你可能有个问题，为什么外界干扰只会影响Pk，而不会影响呢？因为从k-1时刻到k时刻，因为外界干扰使概率云变大了，即不确定性增加了，方差变大了。但是概率云的均值是没变的，因为外界干扰是随机添加的，原来的概论云均值是多少，添加干扰后均值还是多少。描述的是均值，而Pk描述的是方差和协方差。所以只有Pk改变了。

6、用测量值来修正预测值

        上面都是我们通过计算来预测系统的下一时刻状态，现在我们再把传感器的测量值加进我们的预测方程中。

        我们上面的预测结果所使用的单位可能和传感器读取的数据不一样，因此我们给和Pk乘以矩阵Hk，让单位先统一起来：

        传感器的读数也存在误差，且和预测状态一样服从正态分布。该正态分布的均值（最可能的值）就是我们读取到的传感器数值，表示为，传感器的协方差矩阵表示为。

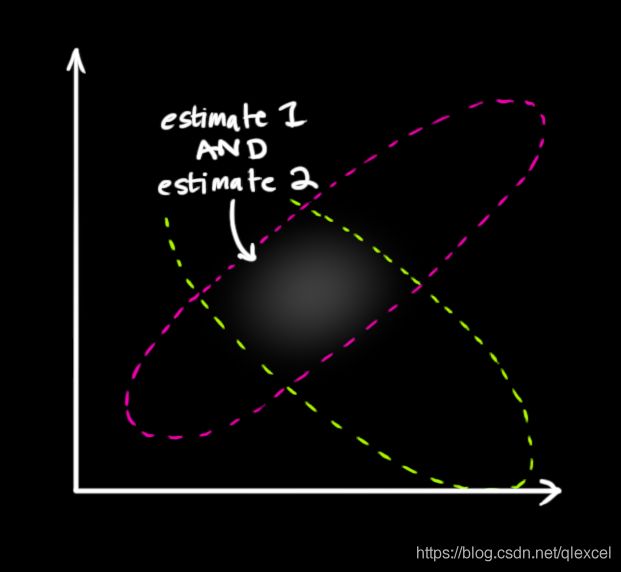
        现在我们有了两个高斯分布，一个是在预测值附近，一个是在传感器读数附近。 

        那么，最有可能的状态是什么呢？对于任何可能的读数，有两种情况：（1）传感器的测量值；（2）由前一状态得到的预测值。如果我们想知道这两种情况都可能发生的概率，将这两个高斯分布相乘就可以了。 

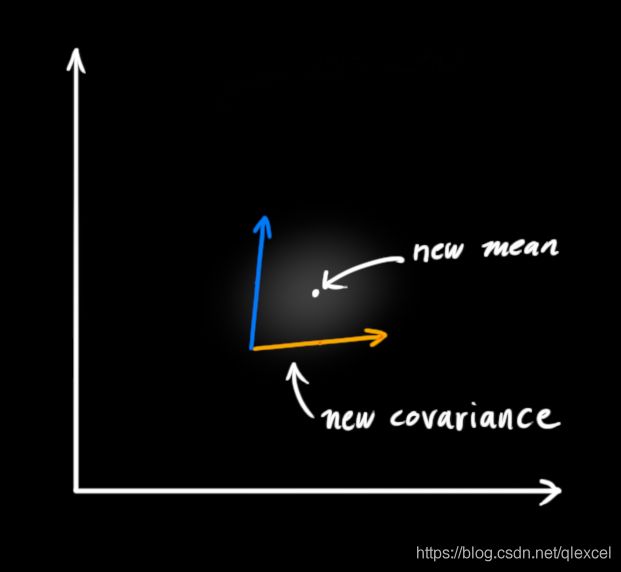
        剩下的就是重叠部分了，这个重叠部分的均值就是两个估计最可能的值，也就是给定的所有信息中的最优估计。

        这个重叠的区域又是另一个高斯分布。它具有新的均值和方差。

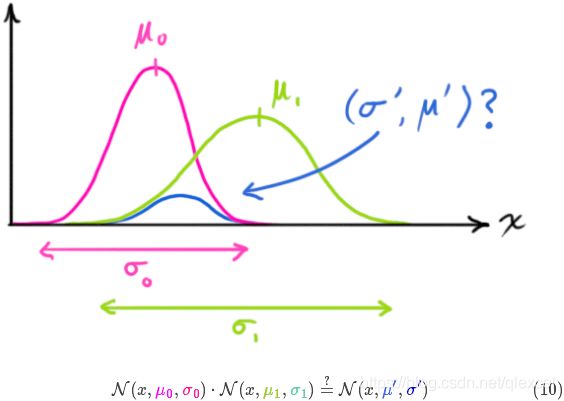
7、融合高斯分布

先以一维高斯分布来分析比较简单点，具有方差  和 μ 的高斯曲线可以用下式表示：

如果把两个服从高斯分布的函数相乘会得到什么呢？ 

将式（9）代入到式（10）中（注意重新归一化，使总概率为1）可以得到： 

将式（11）中的两个式子相同的部分用 k 表示： 

下面进一步将式（12）和（13）写成矩阵的形式，如果 Σ 表示高斯分布的协方差， 表示每个维度的均值，则： 

矩阵K称为卡尔曼增益，下面将会用到。

8、将所有公式整合起来

我们有两个高斯分布，预测部分：

和测量部分：

将它们放到式（15）中算出它们之间的重叠部分：

由式（14）可得卡尔曼增益为： 

将式（16）和式（17）的两边同时左乘矩阵的逆（注意里面包含了矩阵Hk）将其约掉，再将式（16）的第二个等式两边同时右乘矩阵  的逆得到以下等式： 

上式给出了完整的更新步骤方程。就是新的最优估计，我们可以将它和放到下一个预测和更新方程中不断迭代。 

三、总结

1、应用时，只需要关注下面5个式子：

转化为方程：

        X(k|k-1)=A X(k-1|k-1)+B U(k)………(1)
　　式(1)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为某刻状态的控制量，如果没有控制量，它可以为0。
　　到某刻为止，系统结果已经更新了，可是，对应于X(k|k-1)的covariance还没更新。用P表示covariance：
        P(k|k-1)=A P(k-1|k-1) A’+Q………(2)
        式(2)中，P(k|k-1)是X(k|k-1)对应的covariance，P(k-1|k-1)是X(k-1|k-1)对应的covariance，A’表示A的转置矩阵，Q是系统过程的covariance。式子1，2就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。
        某刻有了某刻状态的预测结果，然后再收集某刻状态的测量值。结合预测值和测量值，可以得到某刻状态(k)的最优化估算值X(k|k)：
        X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)
　　其中Kg为卡尔曼增益(Kalman Gain)：
        Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)
　　到某刻为止，已经得到了k状态下最优的估算值X(k|k)。但是为了要另卡尔曼滤波器不断的运行下去直到系统过程结束，还要更新k状态下X(k|k)的covariance：
        P(k|k)=（I-Kg(k) H）P(k|k-1) ……… (5)
　　其中I 为1的矩阵，对于单模型单测量，I=1。当系统进入k+1状态时，P(k|k)就是式子(2)的P(k-1|k-1)。这样，算法就可以自回归的运算下去。

2、卡尔曼滤波本质就是把两个有误差的测量值，看出两个高斯分布，然后求他们重叠的部分，再把重叠的部分看成一个高斯分布，求其均值，得到结果。

四、代码

        下面举一个自平衡小车应用卡尔曼滤波的例子。关于自平衡小车可以参考 自平衡小车
        要让小车平衡需要得到其倾角，测量倾角可以通过加速度计，也可以通过陀螺仪。加速度计可以直接得到倾角值，而陀螺仪只能测量角度变化速度，因此只能对其积分来得到倾角值。
        于是我们通过两个传感器就得到了两个倾角值，他们都有误差，我们更相信谁呢？这个时候就可以用到卡尔曼滤波了。
        在上面的讲解中，为了得到小机器人的状态，我们把通过计算得到的预测值和通过传感器测量的值进行卡尔曼滤波。下面我们把陀螺仪测量的倾角看成预测值，加速度计测量的倾角看成传感器的测量值，来编写代码。

代码如下：

#include "Kalman.h"


/********************************************************************************************************
*	函 数 名：Kalman
*	功能说明：卡尔曼滤波初始化
*	形    参：无
*	返 回 值：无
********************************************************************************************************/ 
void Kalman(void) {
    Q_angle = 0.001f;   //陀螺仪测量值的外界干扰
    Q_bias = 0.003f;    //陀螺仪测量值的外界干扰
    R_measure = 0.03f;  //加速度计测量值的外界干扰

    angle = 0.0f;       //小车倾角
    bias = 0.0f;        //陀螺仪测量值的零偏，即小车不动时，陀螺仪的读数

    P[0][0] = 0.0f;     //协方差矩阵
    P[0][1] = 0.0f;
    P[1][0] = 0.0f;
    P[1][1] = 0.0f;
};

/********************************************************************************************************
*	函 数 名：getAngle
*	功能说明：使用卡尔曼滤波对测量数据进行处理，输出更新后的角度
*	形    参：newAngle--测量到的角度值（使用加速度计测量得到），单位为度
              newRate---测量到的角度变化值（使用陀螺仪测量得到），单位为度每秒
			  dt--------计算间隔，即调用本函数的周期时间，单位为秒
*	返 回 值：通过卡尔曼滤波后的小车倾角
********************************************************************************************************/ 
float getAngle(float newAngle, float newRate, float dt) {
    float S;
    float K[2];                    // Kalman gain - This is a 2x1 vector	
    float y;
    float P00_temp,P01_temp;
	
    //对应第一个式子：X(k) = AX(k-1) + Bu(k-1)
    //根据陀螺仪测量值来计算k时刻倾角
    rate = newRate - bias;        //陀螺仪的读数减去零偏
    angle += dt * rate;           //陀螺仪的读数是角度变化速度，乘以变化时间就得到角度变化量，
                                  //再加上前一次测量的倾角，就得到小车当前的倾角

    //对应第二个式子：P(k) = AP(k-1)A’ + Q
    //计算k时刻协方差矩阵
    P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);
    P[0][1] -= dt * P[1][1];
    P[1][0] -= dt * P[1][1];
    P[1][1] += Q_bias * dt;

    //对应第三个式子：K(k)= P(k-1)H’/(HP(k-1)H’ + R)
    //计算卡尔曼增益
    S = P[0][0] + R_measure; // Estimate error        
    K[0] = P[0][0] / S;
    K[1] = P[1][0] / S;

    //对应第四个式子：X(k)= X(k-1)+Kg(k)(Z(k)- HX(k-1))
    //根据卡尔曼增益修正倾角值
    y = newAngle - angle; //newAngle是加速度计测量的倾角，angle是陀螺仪测量的倾角
    angle += K[0] * y;          //修正倾角  
    bias += K[1] * y;           //修正零偏

    //对应第五个式子：P(k)=（1-Kg(k)H）P(k-1)
    //更新协方差矩阵
    P00_temp = P[0][0];
    P01_temp = P[0][1];

    P[0][0] -= K[0] * P00_temp;
    P[0][1] -= K[0] * P01_temp;
    P[1][0] -= K[1] * P00_temp;
    P[1][1] -= K[1] * P01_temp;

    return angle;    //返回经过卡尔曼滤波处理的倾角
};

1、卡尔曼第一个公式，根据k-1时刻状态预测k时刻状态:

X(k) = AX(k-1) + Bu(k-1) + w(k-1)

建立该模型是测量角度的，但是陀螺仪在没有转向时也有电压输出也就是零偏（bias）

建立矩阵：

angle = angle + (newRate – bias) * dt 推算现角度 = 原角度 + 角速度×时间间隔

bias = bias 不会受到陀螺仪转向的影响认为上一刻的值

转换成矩阵描述：

其中：

 => X(k)

 => A

 => B

newRate => u(k)

w(k) 不确定误差没有考虑

 

对应代码：

rate = newRate – bias; //bias 角速度零偏

angle += dt * rate; //推算现角度 = 原角度 + 角速度×时间间隔

 

2、卡尔曼第二个公式，计算k时刻的协方差矩阵:

P(k) = AP(k-1)A’ + Q

 => P(k)

 => A

 => A’

Q是 的协方差矩阵，表示为

因为零偏噪声和角度噪声是相互独立的，所以cov(angle,bias)=cov(bias,angle)=0

cov(x,x)即方差所以Q 转换成 

做矩阵运算后得到：

 

对应代码：

P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);//由于dt较小所以没有考虑p11×dt×dt

P[0][1] -= dt * P[1][1];

P[1][0] -= dt * P[1][1];

P[1][1] += Q_bias * dt;

 

这里有个问题:根据公式推导p00中的 Q_angle和p11中的 Q_bias没有乘以dt，为什么乘以dt?

 

3、卡尔曼第三个公式计算卡尔曼增益:

K(k)= P(k-1)H’/(HP(k-1)H’ + R)

其中H是测量值和实际值的转换关系是一个放缩关系，

相对于 矩阵，angle和测量值比较没有进行放缩所以是 1，bias没有测量值所以是0

所以对应的 带入得到：

 => K(k)

R 观测噪声误差是常数

做矩阵运算后得到：

K(angle) = p00/(p00 + R)

K(bias) = p10/(p00 + R)

 

对应代码：

S = P[0][0] + R_measure; // Estimate error

K[0] = P[0][0] / S;

K[1] = P[1][0] / S;

 

4、卡尔曼第四个公式根据，卡尔曼增益修正倾角:（可以把卡尔曼增益看成是权重，根据卡尔曼增益决定是更相信加速度计还是更相信陀螺仪）

X(k)= X(k-1)+Kg(k)(Z(k)- HX(k-1))

其中Z(k)是测量矩阵

做矩阵运算后得到：

 

对应代码：

y = newAngle - angle; // Angle difference

angle += K[0] * y;

bias += K[1] * y;

 

5、卡尔曼第五个公式，更新协方差矩阵:

P(k)=（1-Kg(k)H）P(k-1)

做矩阵运算后得到：

对应代码：

P00_temp = P[0][0];

P01_temp = P[0][1];

P[0][0] -= K[0] * P00_temp;

P[0][1] -= K[0] * P01_temp;

P[1][0] -= K[1] * P00_temp;

P[1][1] -= K[1] * P01_temp;