PNN神经网络

**一、导入

Embedding+MLP结构是DNN应用在CTR预估的标准模式。通常，NN层之间都使用“add operation” ，通过激活函数来引入非线性。作者认为，单纯的“add”也许不足以捕获不同的Filed特征间的相关性，原文表述为："The ‘add’ operations of the perceptron layer might not be useful to explore the interactions of categorical data in multiple fields. ”

文中指出，一些相关研究表明“product”相比“add”能更好得捕捉特征间的dependence，因此作者希望在NN中显示地引入“product”操作，从而更好地学习不同Field特征间的相关性，在DNN结构中引入product layer即是这样的一个尝试。

二、模型实战

作者提出Product-based Neural Network（PNN），PNN的结构非常直观，如下图所示：

图1. PNN网络结构

PNN与标准的「Embedding+MLP」差异仅在于引入了Product Layer。上图中Product Layer左边Z部分其实就是将Embedding层学到的嵌入直接原封不动地搬来，右边P部分才是我们讨论的重点。注意，product layer 中每个节点（见蓝色节点）是两两Field的embedding对应的“product”结果，而非所有Field的。

根据 product 函数的不同选择，PNN也有不同实现，这里的想象空间就很多了。文中尝试了相对常见的向量内积（inner product）和外积（outer product），对应 IPNN 和OPNN。

虽然结构简单，但这里存在一个大问题：product层的节点数至少是输入Field数的平方级别。在业界现实场景中，输入Field的规模往往很大，这大大增加了网络复杂度，对PNN的实际落地构成了挑战。作者把L1层每个节点的输入来源拆分为两部分，分别来自Embedding层与Product层，具体地，此时 L1层的输出l1表示为：

其中
对应来自Embedding层和Product层的计算结果，需要优化的正是Lp 部分。

IPNN

IPNN在product层使用向量内积操作，从矩阵视角看，此时结果可以等价表示为：

其中 N表示输入的Field个数，
表示第i个Field的embedding向量。L1层来自product layer部分的输出为
以第 d 个节点为例：

其中
表示第d 个节点连接product层的权重，
表示矩阵逐项乘后全部相加。注意到，
都是对称矩阵，类似FM，可以利用一阶矩阵分解来近似
从而降低复杂。假设
，可得：

其中
此时L1 层的空间复杂度由
时间复杂度由
。NN的输入维度N通常远大于嵌入维度M ，通过一阶矩阵分解，L1 层的复杂度由

这种做法本质上是利用参数共享降低了参数量，更一般地，为了减少信息丢失，可以按需要考虑K-阶分解，当然复杂度也会相应提升K倍，这是一个trade-off。

OPNN

当product层使用外积时，每次计算得到的结果是一个矩阵，即
，这种复杂度这比 IPNN 更严峻。作者简单地使用sum pooling降低复杂度，product层结果为：

这时L1层的时空复杂度都由
，但信息损失也挺严重。

降低复杂度的具体策略与具体的product函数选择有关，IPNN其实通过矩阵分解，“跳过”了显示的product层，通过代数转换直接从embedding层一步到位到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TEIPuZcE-1613575218244)(https://www.zhihu.com/equation?tex=L_1)] 隐层，而OPNN则是直接在product层入手进行优化。

三、Experiment

• 实验设置

数据集 论文使用2个真实世界的开源数据集，具体如下

1. Criteo 含1TB的点击日志，使用连续7天的数据训练，紧接着的下1天作测试。经过negative dawn-sampling和特征映射后，最终包含79.38 M 样本及 1.64M 维特征。
2. iPinyou 包含超过10天的点击日志，共 19.5M 样本，经过one-hot后特征共 937.67 K维。沿用该数据集原始的train/test划分，即每个advertiser的最后3天数据作test，其余作train。

对比方法 使用 logistic loss，论文对比了LR、FM、CCPM、FNN、IPNN、OPNN以及PNN*，PNN*表示同时加入内积和外积。

1. FM和NN模型的embedding维度设为10。
2. 为防止拟合，LR和FM使用L2正则，NN类模型使用rate=0.5的Dropout。
3. CCPM——1嵌入层+2卷积层 (max pooling) +1隐层；FNN——1嵌入层+3隐层；PNN——1嵌入层+1 product层+3隐层。

• 实验结果

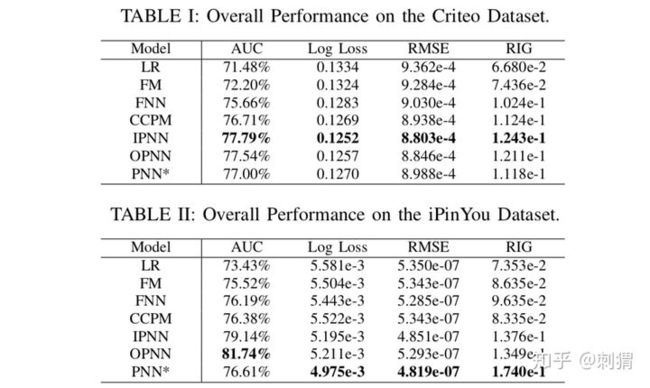
不同数据集和指标上的结实验果如下表所示，PNN类模型性能最优

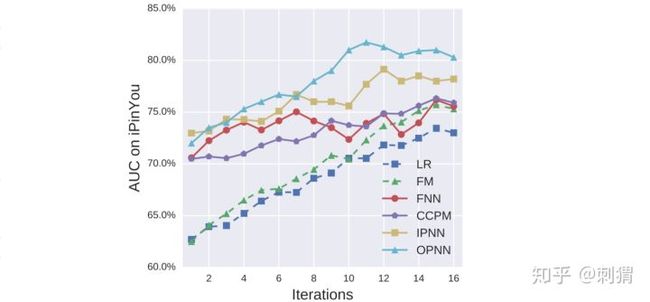
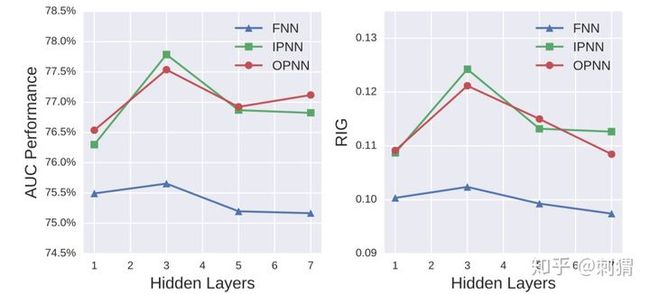
论文也做了其他补充实验。在iPinYou数据集上，各模型在不同迭代轮数下的Auc曲线如图2所示，可见PNN模型的收敛速度在iPinYou上也优于其他算法。使用不同的隐层depth和不同类型激活函数，实验结果分别如图3和图4所示。

图2

图3

图4

四、Conclusion

1. PNN的动机很直观，通过在NN的嵌入层和隐层之间引入product层，显示地引入基于field的“product”，从而加强单纯基于“add”的NN的特征相关性学习能力。

2. product函数的选择有不少想象空间；而引入product后的模型复杂度，将直接影响落地可行性。构造怎样的product函数以及如何降低复杂度是使用product layer的关键，例如文中对IPNN和OPNN的处理。一个实用的落地trick是基于先验知识，只在指定的Field间作product，从而降低复杂度，当然这也导致了需要human effort的坑。