TripletMarginLoss原理和源码实现

TripletMarginLoss最早是在 FaceNet 提出的，它是用于衡量不同人脸特征之间的距离，进而实现人脸识别和聚类

现在被广泛应用于不同业务场景中，比如推荐场景和搜索场景下的向量召回模型。TripletMarginLoss的公司如下：$$L(a,p,n)=max\{d(a,p)-d(a,n)+marge,0\}$$,其中d默认表示欧氏距离。
该Loss针对不同样本配对，有以下三种情况：
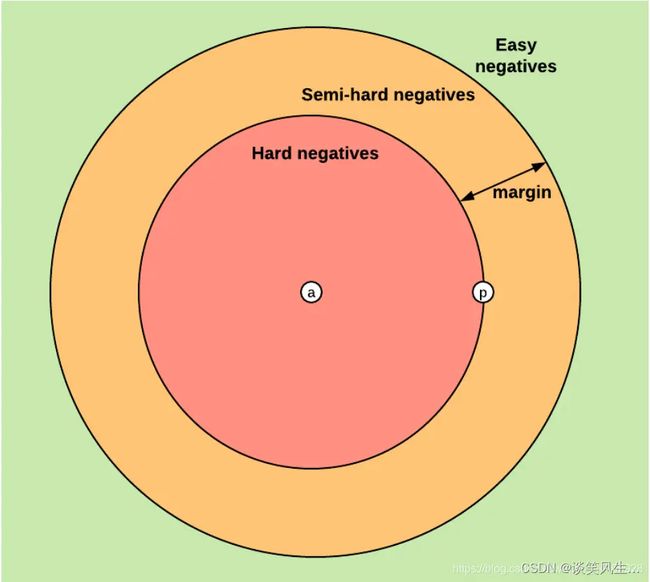
1.简单样本，即$$d(a_i,p_i)-d(a_i,n_i)+marge<0$$此时 正样本距离anchor的距离$d(a_i,p_i)+Margin$仍然小于负样本距离anchor的距离$d(a_i,n_i)$,该情况认为正样本距离足够小，不需要进行优化，因此Loss为0;

2.难样本，即$$d(a_i,p_i)-d(a_i,n_i)>0$$此时 负样本距离anchor的距离$d(a_i,n_i)$ 小于 正样本距离anchor的距离$d(a_i,p_i)$，需要进行优化。

半难样本，即$$d(a_i,p_i)-d(a_i,n_i)<0并且d(a_i,p_i)-d(a_i,n_i)+marge>0$$此时虽然 负样本距离anchor的距离$d(a_i, n_i) $大于正样本距离anchor的距离$d(a_i, p_i)$，但是还不够大，没有超过 Margin，需要优化。

此外论文作者还提出了 swap 这个概念，原因是我们公式里只考虑了anchor距离正类和负类的距离，而没有考虑正类和负类之间的距离，考虑以下情况：

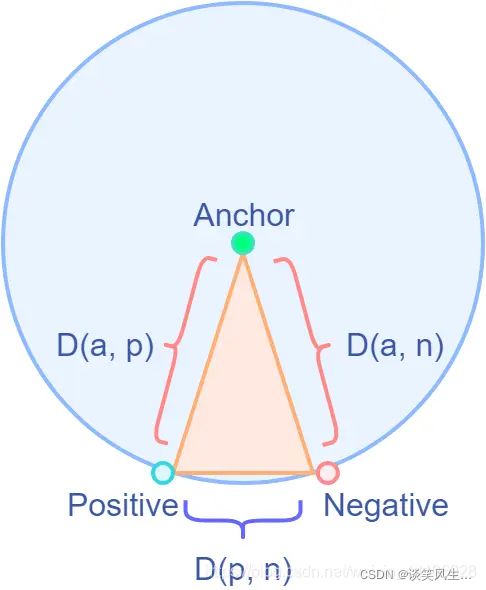
可能Anchor距离正样本和负样本的距离相同，但是负样本和正样本的距离很近，不利于模型区分，因此会做一个swap，即交换操作，在代码里体现的操作是取最小值。

## 伪代码
if swap: 
	D(a, n) = min(D(a,n), D(p, n))

这样取了最小值后，在Loss计算公式中，Loss值会增大，进一步帮助区分负样本。下面是numpy的对应代码:

def np_triplet_margin_loss(anchor, postive, negative, margin, swap, reduction="mean", p=2, eps=1e-6):
    def _np_distance(input1, input2, p, eps):
     # Compute the distance (p-norm)
        np_pnorm = np.power(np.abs((input1 - input2 + eps)), p)
        np_pnorm = np.power(np.sum(np_pnorm, axis=-1), 1.0 / p)
        return np_pnorm

    dist_pos = _np_distance(anchor, postive, p, eps)
    dist_neg = _np_distance(anchor, negative, p, eps)

    if swap:
        dist_swap = _np_distance(postive, negative, p, eps)
        dist_neg = np.minimum(dist_neg, dist_swap)
    output = np.maximum(margin + dist_pos - dist_neg, 0)

    if reduction == "mean":
        return np.mean(output)
    elif reduction == "sum":
        return np.sum(output)
    else:
        return output