(01)ORB-SLAM2源码无死角解析-(10)ORBextractor::operator()→灰度质心法

讲解关于slam一系列文章汇总链接:史上最全slam从零开始，针对于本栏目讲解的(01)ORB-SLAM2源码无死角解析链接如下(本文内容来自计算机视觉life ORB-SLAM2 课程课件):
(01)ORB-SLAM2源码无死角解析-(00)目录_最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/123092196
 
$文末正下方中心提供了本人联系方式，点击本人照片即可显示WX\to 官方认证$
 

一、前言

在上一篇博客中，我们讲解了关键点的均匀化，最后还提及到灰度质心法。那么什么是灰度质心法，其作用是用于什么?

FAST关键点，是缺少角度信息的，其会对描述子产生影响，因为描述子需要具备旋转不变性(该内容的核心再后面的章节会进行讲解)，我们首要的问题是为关键点提供角度信息。

 

二、理论介绍

第一步:
我们定义该区域图像的矩
$$\sum _{x,y}{x}^p{y}^{q}I(x,y)，p,q=\{0,1\}$$式中 $p,q$ 取0或者1；$I(x,y)$表示在像素坐标 $(x,y)$ 处图像的灰度值l; $m_{pq}$表示图像的矩。在半径为$R$的圆形图像区域，沿两个坐标轴$(x,y)$方向的图像矩分别为:
$$m_{10}=\sum _{x=-R}^R\sum _{y=-R}^{R}xI(x,y)$$$$m_{01}=\sum _{x=-R}^R\sum _{y=-R}^{R}yI(x,y)$$圆形区域内所有像素的灰度值总和为:
$$m_{00}=\sum _{x=-R}^R\sum _{y=-R}^{R}I(x,y)$$

第二步:
图像的质心为:$$C=(c_x,c_y)=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})$$

第三步:
关键点的"主方向"就可以表示为从圆形图像形心 $O$ 指向质心 $C$ 的方向向量 $OC$，于是关键点的旋转角度记为：
$$\theta =arctan2(x_y,c_x)=arctan2(m_{01},m_{10})$$以上就是灰度质心法求关键点旋转角度的问题。下图 $P$ 为几何中心，$Q$ 为灰度质心：

 
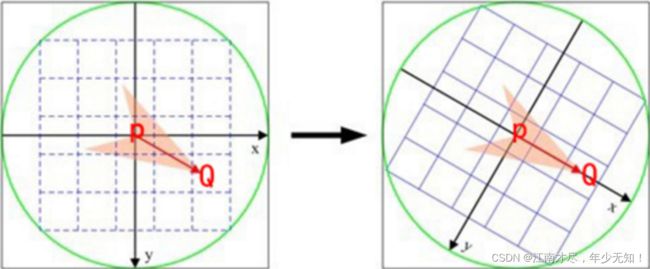
思考:
为什么计算灰度质心的时候，是选择一个圆中的像素，而不是一个正方形。这是因为圆具备旋转不变的性质。比如说，一张图像中确定一个像素的质心之后，图像发生了旋转。这个时候，如果我们选择以该像素为中心，计算正方形区域内的像素的矩$m_{01}$,$m_{10}$,$m_{00}$就会发生变化，这样质心就发生改变。但是如果计算圆内的像素。只要半径保持不变，那么他的像素就不会发生变化。如下图所示：

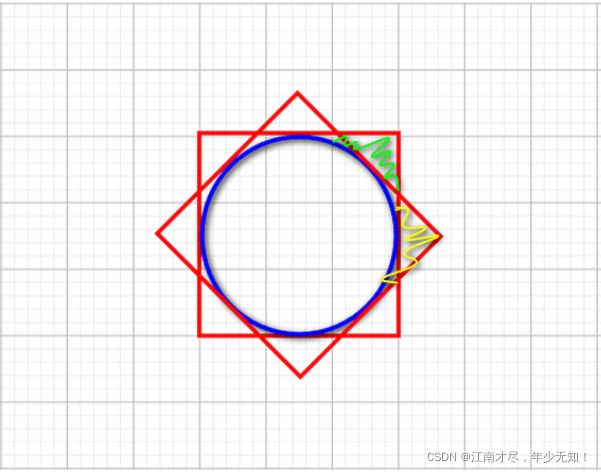
可以看到正方形旋转的时候，蓝色与黄色区域的像素是不一样的。
 

三、代码流程

代码中计算灰度质心的时候，还采用了一些其他的技巧，下面是一个简单的图示:

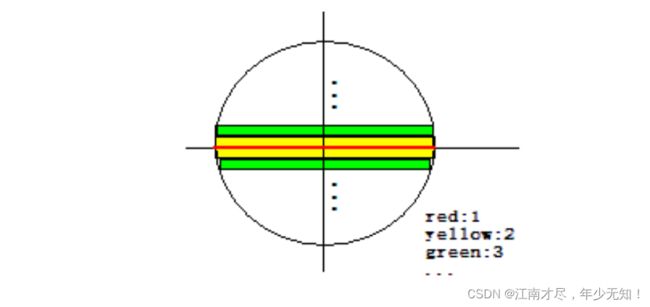
比如说源码求 $m_{00}$ 的时候，其需要计算圆内所有像素值的总和，其是先求红色行像素值总和(一列)，然后在求黄色列像素值总和(两列)，再接着求绿色列总和(两列)。依次递推下去。然后把所有列的和相加起来，就是圆内像素值的总和。

使用这种方式进行计算，在代码实现的时候，就需要一些已知量，比如黄色列的坐标索，或者说知道黄色列这一列一共有多少个像素。代码中是如何实现计算的呢，我们先来看下图：

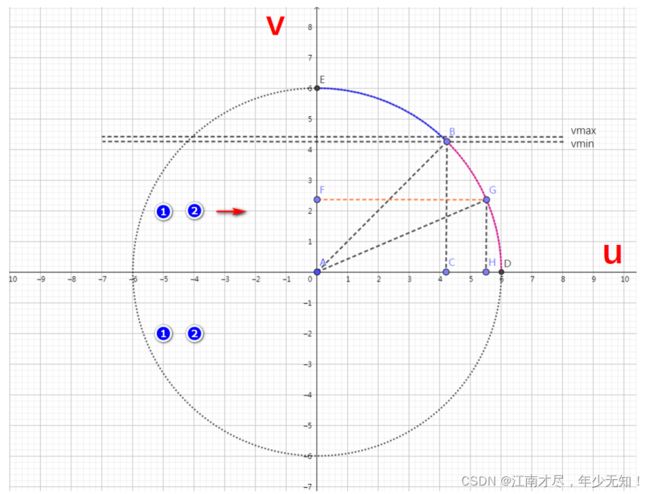
上图的 $V,U$ 分别表示坐标轴，以及圆的半径，然后使用勾股定理进行计算。但是代码中用到了一个技巧，就是只用对称的方式进行计算，以 AB 为对称轴进行计算。该坐标的计算代码位于 src/ORBextractor.cc 的 ORBextractor::ORBextractor() 函数中，该函数我们在前面的博客中有进行讲解过:

ORBextractor::ORBextractor(int _nfeatures,		//指定要提取的特征点数目
                           float _scaleFactor,	//指定图像金字塔的缩放系数
                           int _nlevels,		//指定图像金字塔的层数
                           int _iniThFAST,		//指定初始的FAST特征点提取参数，可以提取出最明显的角点
                           int _minThFAST):		//如果初始阈值没有检测到角点，降低到这个阈值提取出弱一点的角点
    nfeatures(_nfeatures), scaleFactor(_scaleFactor), nlevels(_nlevels),
    iniThFAST(_iniThFAST), minThFAST(_minThFAST)//设置这些参数
{
	......
	......
	......
   //This is for orientation
    //下面的内容是和特征点的旋转计算有关的
    // pre-compute the end of a row in a circular patch
    //预先计算圆形patch中行的结束位置
    //+1中的1表示那个圆的中间行
    umax.resize(HALF_PATCH_SIZE + 1);
    
    //cvFloor返回不大于参数的最大整数值，cvCeil返回不小于参数的最小整数值，cvRound则是四舍五入
    int v,		//循环辅助变量
        v0,		//辅助变量
        vmax = cvFloor(HALF_PATCH_SIZE * sqrt(2.f) / 2 + 1);	//计算圆的最大行号，+1应该是把中间行也给考虑进去了
                //NOTICE 注意这里的最大行号指的是计算的时候的最大行号，此行的和圆的角点在45°圆心角的一边上，之所以这样选择
                //是因为圆周上的对称特性
                
    //这里的二分之根2就是对应那个45°圆心角
    
    int vmin = cvCeil(HALF_PATCH_SIZE * sqrt(2.f) / 2);
    //半径的平方
    const double hp2 = HALF_PATCH_SIZE*HALF_PATCH_SIZE;

    //利用圆的方程计算每行像素的u坐标边界（max）
    for (v = 0; v <= vmax; ++v)
        umax[v] = cvRound(sqrt(hp2 - v * v));		//结果都是大于0的结果，表示x坐标在这一行的边界

    // Make sure we are symmetric
    //这里其实是使用了对称的方式计算上四分之一的圆周上的umax，目的也是为了保持严格的对称（如果按照常规的想法做，由于cvRound就会很容易出现不对称的情况，
    //同时这些随机采样的特征点集也不能够满足旋转之后的采样不变性了）
    for (v = HALF_PATCH_SIZE, v0 = 0; v >= vmin; --v)
    {
        while (umax[v0] == umax[v0 + 1])
            ++v0;
        umax[v] = v0;
        DEBUG("%d=%d", v, v0);
        ++v0;
    }

比如这里的半径 HALF_PATCH_SIZE = 15, 其计算出来的 umax 数值为:

	umax[0] == 15
	umax[1] == 15
	umax[2] == 15
	umax[3] == 15
	umax[4] == 14
	umax[5] == 14
	umax[6] == 14
	umax[7] == 13
	umax[8] == 13
	umax[9] == 12
	umax[10] == 11
	umax[11] == 10
	umax[12] == 9
	umax[13] == 8
	umax[14] == 6
	umax[15] == 3

其上 $umax[0]==15$ 意思表示，当 $V=0$，在该行参数计算的像素个数为15个($U>0方向上$)。 $umax[1]==15$ 意思表示，当 $V=1$，在该行参与计算的像素个数为15个($U>0方向上$), 依次递推。

 

四、源码注释

灰度质心角度计算于 src/ORBextractor.cpp 中被 ORBextractor::ComputeKeyPointsOctTree() 调用，其函数名为 computeOrientation(), 实现具体过程图下:

/**
 * @brief 计算特征点的方向
 * @param[in] image                 特征点所在当前金字塔的图像
 * @param[in & out] keypoints       特征点向量
 * @param[in] umax                  每个特征点所在图像区块的每行的边界 u_max 组成的vector
 */
static void computeOrientation(const Mat& image, vector<KeyPoint>& keypoints, const vector<int>& umax)
{
    // 遍历所有的特征点
    for (vector<KeyPoint>::iterator keypoint = keypoints.begin(),
         keypointEnd = keypoints.end(); keypoint != keypointEnd; ++keypoint)
    {
        // 调用IC_Angle 函数计算这个特征点的方向
        keypoint->angle = IC_Angle(image, 			//特征点所在的图层的图像
                                   keypoint->pt, 	//特征点在这张图像中的坐标
                                   umax);			//每个特征点所在图像区块的每行的边界 u_max 组成的vector
    }
}

/**
 * @brief 这个函数用于计算特征点的方向，这里是返回角度作为方向。
 * 计算特征点方向是为了使得提取的特征点具有旋转不变性。
 * 方法是灰度质心法：以几何中心和灰度质心的连线作为该特征点方向
 * @param[in] image     要进行操作的某层金字塔图像
 * @param[in] pt        当前特征点的坐标
 * @param[in] u_max     图像块的每一行的坐标边界 u_max
 * @return float        返回特征点的角度，范围为[0,360)角度，精度为0.3°
 */
static float IC_Angle(const Mat& image, Point2f pt,  const vector<int> & u_max)
{
    //图像的矩，前者是按照图像块的y坐标加权，后者是按照图像块的x坐标加权
    int m_01 = 0, m_10 = 0;

    //获得这个特征点所在的图像块的中心点坐标灰度值的指针center
    const uchar* center = &image.at<uchar> (cvRound(pt.y), cvRound(pt.x));

    // Treat the center line differently, v=0
    //这条v=0中心线的计算需要特殊对待
    //后面是以中心行为对称轴，成对遍历行数，所以PATCH_SIZE必须是奇数
    for (int u = -HALF_PATCH_SIZE; u <= HALF_PATCH_SIZE; ++u)
        //注意这里的center下标u可以是负的！中心水平线上的像素按x坐标（也就是u坐标）加权
        m_10 += u * center[u];

    // Go line by line in the circular patch  
    //这里的step1表示这个图像一行包含的字节总数。参考[https://blog.csdn.net/qianqing13579/article/details/45318279]
    int step = (int)image.step1();
    //注意这里是以v=0中心线为对称轴，然后对称地每成对的两行之间进行遍历，这样处理加快了计算速度
    for (int v = 1; v <= HALF_PATCH_SIZE; ++v)
    {
        // Proceed over the two lines
        //本来m_01应该是一列一列地计算的，但是由于对称以及坐标x,y正负的原因，可以一次计算两行
        int v_sum = 0;
        // 获取某行像素横坐标的最大范围，注意这里的图像块是圆形的！
        int d = u_max[v];
        //在坐标范围内挨个像素遍历，实际是一次遍历2个
        // 假设每次处理的两个点坐标，中心线下方为(x,y),中心线上方为(x,-y) 
        // 对于某次待处理的两个点：m_10 = Σ x*I(x,y) =  x*I(x,y) + x*I(x,-y) = x*(I(x,y) + I(x,-y))
        // 对于某次待处理的两个点：m_01 = Σ y*I(x,y) =  y*I(x,y) - y*I(x,-y) = y*(I(x,y) - I(x,-y))
        for (int u = -d; u <= d; ++u)
        {
            //得到需要进行加运算和减运算的像素灰度值
            //val_plus：在中心线下方x=u时的的像素灰度值
            //val_minus：在中心线上方x=u时的像素灰度值
            int val_plus = center[u + v*step], val_minus = center[u - v*step];
            //在v（y轴）上，2行所有像素灰度值之差
            v_sum += (val_plus - val_minus);
            //u轴（也就是x轴）方向上用u坐标加权和（u坐标也有正负符号），相当于同时计算两行
            m_10 += u * (val_plus + val_minus);
        }
        //将这一行上的和按照y坐标加权
        m_01 += v * v_sum;
    }

    //为了加快速度还使用了fastAtan2()函数，输出为[0,360)角度，精度为0.3°
    return fastAtan2((float)m_01, (float)m_10);
}

fastAtan2 函数求解出来的结果是一个角度，该结果会复制给关键点对应的 keypoint->angle 参数。

 

五、结语

该篇博客我们了解了如何使用灰度质心法求关键点的角度方向，针对于FAST关键点的相关内容已经讲解得差不多了。前面我们提到ORB特征点由 FAST 关键点以及 BRIEF 描述子组成，下面就是对 BRIEF 的相关内容进行讲解了。
 
 
本文内容来自计算机视觉life ORB-SLAM2 课程课件