Stata——固定效应模型、随机效应模型、混合效应模型(区别、实例)
目录
1 固定效应模型概念(Fixed Effects Model)
1.1 stata命令
1.1.1 LSDV法(Least squares dummy variable)
1.1.2 固定效应模型(Fixed Effects Model)
1.1.3 命令比较(reg、xtreg、areg、reghdfe)
1.2 固定效应模型选择——F检验
1.2.1单因素效应直接看P值
1.2.2双向效应检验(时点效应)
2 随机效应模型(Random Effects Model)
3 混合效应模型(Mixed Effects Model)
——选择使用混合回归还是随机效应
4 豪斯曼检验——个体效应与随机效应选择
5 代码整合
1 固定效应模型概念(Fixed Effects Model)
在面板数据线性回归模型中, 如果对于不同的截面或不同的时间序列, 只是模型的截距项是不同的, 而模型的斜率系数是相同的, 则称此模型为固定效应模型。 固定效应模型分为三类:
1.个体固定效应模型:对于不同的纵剖面时间序列(个体) 只有截距项不同的模型
2.时点固定效应模型:对于不同的截面(时点) 有不同截距的模型。
3.时点个体固定效应模型(双向效应模型):对于不同的截面(时点)、 不同的时间序列(个体) 都有不同截距模型。
模型中加入一系列虚拟变量作为控制变量以达到控制某些特征的目的,这些虚拟变量就叫做固定效应。比如加行业固定效应、年份固定效应、地区固定效应,实则都是加入一连串的行业/年份/地区虚拟变量作为控制变量,以达到对行业/年份/地区特征的控制。
1.1 stata命令
1.1.1 LSDV法(Least squares dummy variable)
* LSDV法
reg y x controls i.industry i.year, cluster(stkcd) // 以“i.”形式加入一系列虚拟变量,但是不生成这些虚拟变量。模型存在双因素效应
reg y x controls i.stkcd, cluster(stkcd) // 模型存在个体效应
reg y x controls i.year, cluster(stkcd) // 模型存在时间效应
xi: reg y x controls i.stkcd i.year, cluster(stkcd) // 加入xi,就是在加入虚拟变量的基础上还会创建这些虚拟变量,个人一般不用。
* 组内估计法
xtset industry year // 需要先设定面板数据
xtreg y x controls i.year, fe robust // fe代表固定效应模型
* 其他方法
areg、reghdfe等对于时间效应,如果样本是以天为单位的股票数据,day的范围跨越了365天,用LSDV就会生成364个虚拟变量,导致结果十分冗长,此时可以用固定效应模型(2.2)来解决这一问题。
因为数据往往存在异方差、自相关等问题,导致估计的标准误不准确,所以我们会使用稳健标准误来替代原始标准误。如代码中使用的**robust(异方差稳健标准误) 和 cluster(聚类文件标准误)**代表的是采用稳健标准误的不同形式。
其中reg+cluster(stkcd) 等价于 xtreg,fe + robust,是目前论文中常用的比较稳健的标准误了,同样,也是比较难显著。稳健和显著很难两全。
1.1.2 固定效应模型(Fixed Effects Model)
- 截面数据:
模型:![]()
reg y x controls i.industry, robust- 混合截面数据
模型:![]()
(xi:) reg y x controls i.industry i.year,robust- 面板数据(固定效应模型)
——个体固定:
——双向固定:
* 法1 xtreg
xtset id year //需要先定义面板数据
xtreg y x controls, fe robust //单因素个体效应
xtreg y x controls, fe i(year) robust // 单因素时间效应模型
xtreg y x controls i.year, fe robust //双向效应模型
* 法2 reghdfe
reghdfe y x controls, absorb(id, year)实例:
xtset industry year //需要先定义面板数据 行业,年份
//被解释变量:lnQ8,解释变量:Q,控制变量:lnQ6 lnQ7
//个体效应和时间效应的固定效应(双向效应)
xtreg lnQ8 Q lnQ6 lnQ7 i.year, fe robust
//固定industry,个体效应
xtreg lnQ8 Q lnQ6 lnQ7 , fe robust双向效应结果:
(行业)个体效应结果:
1.1.3 命令比较(reg、xtreg、areg、reghdfe)
三种命令自变量结果t值和系数都是一样的,区别就在于结果报告的冗长程度。
——reg(普通估计)
- reg最为朴实无华,会全部报告。无论需要控制什么固定效应,直接往模型中以控制变量形式加入即可,Stata均会报告其回归系数。想知道被个体固定效应吸收掉的变量的估计系数用reg
——reghdfe(多维估计)
- reghdfe主要用于实现多维固定效应线性回归。
- 有些时候,我们需要控制多个维度(如城市-行业-年度)的固定效应, 此时,areg的absorb选项中只能加入一个固定效应,如果要加入更多固定效应,除非只能以i.形式加入控制变量,但是这样就与reg、xtreg一样,显的冗余了,且运行速度会很慢;
- reghdfe解决的就是这一痛点,其在运行速度方面远远优于xtreg等命令。
——xtreg, fe(组内估计)
- xtreg, fe是固定效应模型的官方命令,使用这一命令估计出来的系数是最为纯正的固定效应估计量(组内估计量)
- 在使用xtreg命令之前,首先需要使用xtset命令进行面板数据声明,定义截面(个体)维度和时间维度;
- xtreg实现个体固定效应估计必须要跟fe,如果不跟fe,默认为采用随机效应模型进行估计(re)
- 对于不随时间变化的个体异质性都会被fe吸收,比如SOE一般不随时间变化,个体固定效应实际上已经包含了SOE的信息,所以采用xtreg, fe后,SOE将会出现“omit”,表示由于多重共线性被自动省略了。
- 如果要额外控制其他固定效应,必须要在控制变量中加入该效应,比如我需要额外控制年份、地区,命令应当写为:
xtreg invest mvalue kstock i.province i.year, fe
1.2 固定效应模型选择——F检验
1.2.1单因素效应直接看P值
在固定效应模型结果最下方,有显示的F值和P值,如P=0.0000<0.05,拒绝原假设→适用固定效应模型。
1.2.2双向效应检验(时点效应)
双因素效应结果最下方的P值代表个体效应,仅能用于判断是否存在个体效应。
使用stata命令testparm,检验所有的时间虚拟变量系数是否都为0。如下,P=0.0000<0.05,拒绝原假设,即存在时点效应。
testparm i.year //检验所有的时间虚拟变量系数是否都为0结果
2 随机效应模型(Random Effects Model)
随机效应模型认为误差项和解释变量不相关,而固定效应模型认为误差项和解释变量是相关的。
![]()
xtreg lnQ8 Q lnQ6 lnQ7 i.year, re robust3 混合效应模型(Mixed Effects Model)
各个截面估计方程的 截距和斜率项都一样
![]()
//vce(cluster year)表示以“year"为聚类变量的聚类稳健标准误
reg lnQ8 Q lnQ6 lnQ7,vce(cluster year)
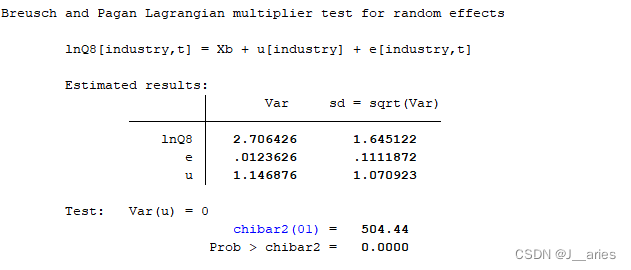
est sto OLS——选择使用混合回归还是随机效应
xttest0reg lnQ8 Q lnQ6 lnQ7,vce(cluster year) //混合效应模型
est sto OLS
xtreg lnQ8 Q lnQ6 lnQ7 i.year, re //随机效应模型
est store re
xttest0检验得到的P 值为0.0000,表明随机效应模型优于混合OLS 模型
- 将三个模型结果放到一起
est table OLS fe re4 豪斯曼检验——个体效应与随机效应选择
原假设是随机效应和固定效应无差异,如果拒绝原假设,则采用固定效应模型,否则为随机效应模型。
由于传统的豪斯曼检验假设球形扰动项,故在进行固定效应与随机效应的估计时,均不使用异方差或聚类稳健的标准误。“constant”表示在比较系数估计值时包括常数项(默认不包括常数项)
xtreg lnQ8 Q lnQ6 lnQ7 , fe //个体固定效应
est store fe //储存命名为fe
xtreg lnQ8 Q lnQ6 lnQ7 , re //随机效应
est store re //储存命名为re
hausman fe re,constant //豪斯曼检验
由于p指为0.0000,故拒绝原假设,认为应该使用固定效应模型,而非随机效应模型。
注:计算出的 s q r t ( d i a g ( V b − V B ) ) sqrt(diag(V_b-V_B)) sqrt(diag(Vb−VB))可能为负。说明的模型设定有问题,导致Hausman 检验的基本假设得不到满足,遗漏变量的问题,或者某些变量是非平稳等等。
可以改用hausman检验的其他形式:hausman fe, sigmaless选项,表示统一使用随机效应估计量的方差估计,可以减少出现负值的可能性。
hausman fe re,constant sigmamore5 代码整合
xtset industry year // 需要先设定面板数据
xtreg lnQ8 Q lnQ6 lnQ7 , re //随机效应模型
est store re //储存命名为re
reg lnQ8 Q lnQ6 lnQ7,vce(cluster year) //混合效应模型
est sto OLS 储存命名为OLS
xttest0 //随机效应模型与混合效应模型选择
xtreg lnQ8 Q lnQ6 lnQ7 , fe //个体固定效应
est store fe //储存命名为fe
hausman fe re,constant //豪斯曼检验,选择个体固定效应还是随机效应模型
est table OLS fe re //将三个模型结果整合在一起本文参考:02 固定效应模型与Stata实现_黑百椰的博客-CSDN博客_stata固定效应
【Python+Stata】豪斯曼检验:固定效应or随机效应?_Python for Finance的博客-CSDN博客_stata 豪斯曼检验