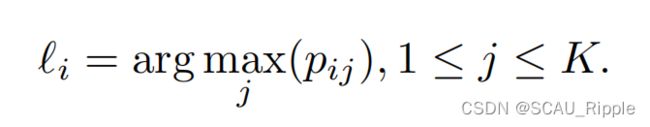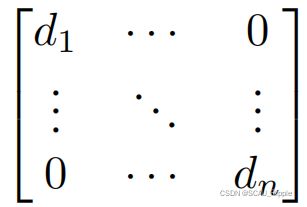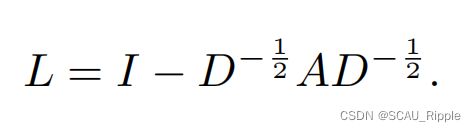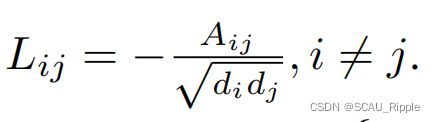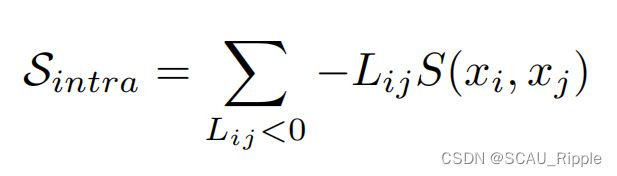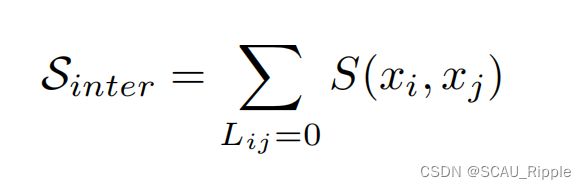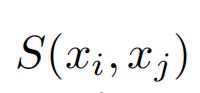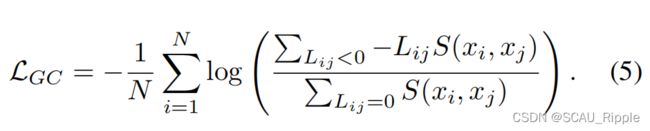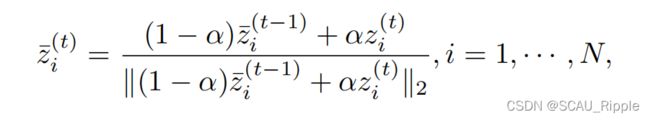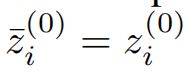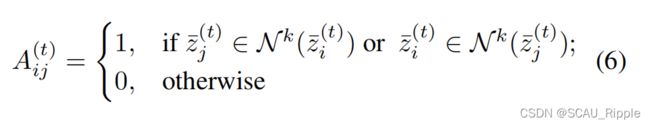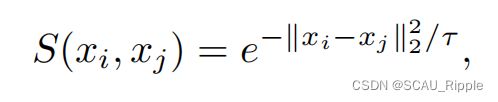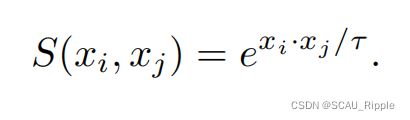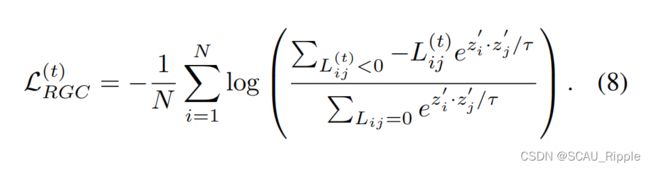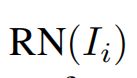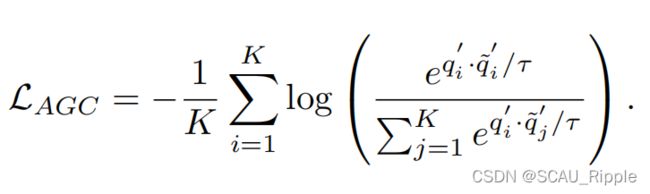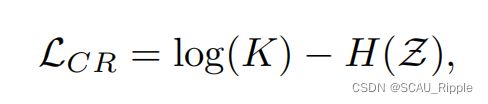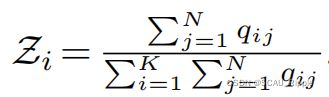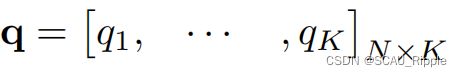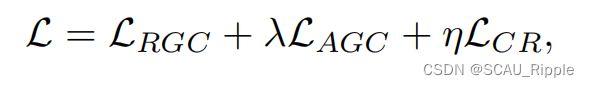不吃香菜的zbw

论文阅读“Graph Contrastive Clustering”（ICCV2021）

论文标题

Graph Contrastive Clustering

论文作者、链接

作者：Zhong, Huasong and Wu, Jianlong and Chen, Chong and Huang, Jianqiang and Deng, Minghua and Nie, Liqiang and Lin, Zhouchen and Hua, Xian-Sheng

链接：ICCV 2021 Open Access Repository

代码：GitHub - mynameischaos/GCC: Graph Contrastive Clustering (ICCV2021)

Introduction逻辑

论文动机&现有工作存在的问题

有监督的学习需要标签，这意味着需要大量人力去标注

聚类作为无监督学习不需要标签，但是有两个明显的缺点1.对特征无区别2.特征提取和聚类过程分离导致次优解

现有模型学到的特征区别度不够高，没有将潜在的类别信息加入模型

论文核心创新点

假设一个簇中的样本及其增广样本，应该共享相似的特征表示和聚类分配

构造一个基于当前特征的相似图，然后将其应用于表示学习和聚类学习

考虑了潜在类别信息

将图对比学习框架应用于聚类任务设计了GCC，提出拉普拉斯图对比损失 the graph Laplacian based contrastive loss

相关工作

深度聚类

对比学习

论文方法

一组无标签图片集 $\textbf{I}=\{I_1,...,I_N\}$ ，有K个类别

学习一个映射函数 $\phi$ 参数为 $\theta$ ，将图片映射到，其中是d维的特征向量，并且有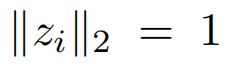约束，然后是K维的概率分布，满足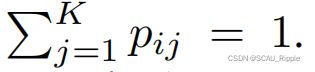，也就是分配给所有簇的概率之和为1。根据下列公式计算簇的分配

图对比 Graph Contrastive (GC)

定义无向图，其中V是顶点集，边集E可以用邻接矩阵A表示：

将定义为的阶数，则有D矩阵为：

则G的归一化对称图拉普拉斯算子可定义为:

很容易验证到有

对于N个特征 $\textbf{x}=\{x_1,...,x_N\}$ ，在2范数的约束下，如果i与j的领接矩阵 $A_{ij}>0$ 则与应该尽量靠近，如果 $A_{ij}=0$ 则远离。假设图可以被划分为几个区，则同一个区中的特征表示的相似性应该比区之间的相似性大，即同区内的特征相似性比区之间大。有如下定义

则一个区内的相似性总和为

其中是和的相似性计算。于是，对于图对比的损失可以定义为

对进行最小化，可以使得网络同时增大区内相似性并且减小区间相似性

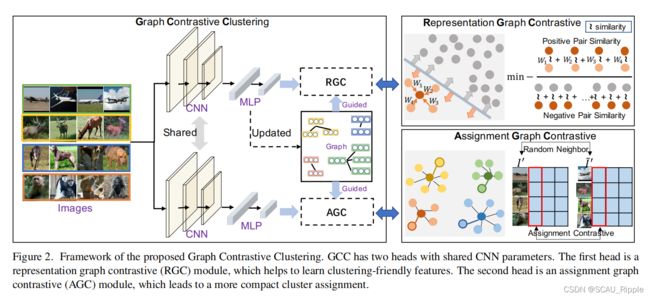
图对比聚类 Graph Contrastive Clustering(GCC)

图特征对比representation graph contrastive (RGC)，基于图特征对比学习，学习聚类友好特征。

图分配对比assignment graph contrastive (AGC)，利用聚类级图对比学习实现最后的聚类分配。

在构造图之前，利用移动平均移动来减少模型波动带来的特征学习偏差

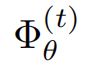代表模型，并且 $Z^{(t)}= \left(z_{1}^{(t)}, \cdots, z_{N}^{(t)}\right)=\left(\Phi_{\theta}^{(t)}\left(I_{1}\right), \cdots, \Phi_{\theta}^{(t)}\left(I_{N}\right)\right)$ 代表第t个epoch学到的特征表示，则特征表示的平均移动定义为：

其中， $\alpha$ 是用来权衡当前和过去的影响的参数，有

用下公式来构建KNN图

其中 $i,j \in \{1,...,N\}$ 。由此可以得到归一化的拉普拉斯算子 $L^{(t)}$

相似函数

使用谱聚类中常用的高斯核函数Gaussian kernel function，来计算两个样本中的相似性

其中 $\tau$ 表示方差或者是温度参数。

因为有 $\left\|x_{i}x_{j}\right\|_{2}^{2}=\left\|x_{i}\right\|_{2}^{2}+\left\|x_{j}\right\|_{2}^{2}-2 x_{i} \cdot x_{j}=$ $2-2 x_{i} \cdot x_{j}$

于是相似函数由上式变成下式

图表示对比

假设有一组经过随机数据增广的图片组 $\mathbf{I}^{\prime}=\left\{I_{1}^{\prime}, \ldots, I_{N}^{\prime}\right\}$ ，并且其对应的特征为 $\mathbf{z}^{\prime}=\left\{z_{1}^{\prime}, \ldots, z_{N}^{\prime}\right\}$ 。根据之前提到的，如果两点在图谱中是相连的，那么 $z^{\prime}_i$ 和 $z^{\prime}_j$ 应该尽可能相似

在公式（5）中，令 $x=z^{\prime}$ ，则得到RGC的损失函数

图分配对比

传统的基于聚类的对比学习，图片和它们的增广结果应该尽可能分配到同一个簇中。在模型学习的过程中，图片及其邻居将会有高置信度的簇分配结果。

假设有一组经过随机数据增广的图片组 $\mathbf{I}^{\prime}=\left\{I_{1}^{\prime}, \ldots, I_{N}^{\prime}\right\}$ ，并且 $\tilde{\mathbf{I}}^{\prime}=\left\{\tilde{I}_{1}^{\prime}, \ldots, \tilde{I}_{N}^{\prime}\right\}$ 满足 $\tilde{\mathbf{I}}^{\prime}_j$ 是根据图 $A^{(t)}$ 随机选择的一个邻居 $I^{\prime}$ 。则对于 $I^{\prime}$ 和 $\tilde{\mathbf{I}}^{\prime}$ 的概率分配矩阵为

其中表示的随机选择的邻居，然后将它们变成列向量的形式

那么， $q^{\prime}_i$ 和 $\tilde{q}^{\prime}_i$ 表示 $I^{\prime}$ 和 $\tilde{\mathbf{I}}^{\prime}$ 中的哪一张图片将会被分配给第i个簇，则AGC的损失函数定义为

聚类正则化损失

为了防止将所有的样本分配给同一个簇，则需要进行聚类正则化，有

其中，以及是 $\textbf{I}$ 的分配概率。

全局损失函数为

其中 $\lambda$ 和 $\eta$ 是超参

算法流程

消融实验设计

图表对比损失的影响

聚类正则化损失的影响

自标签精调的影响

一句话总结

从图谱的内部关系入手，设计了对比学习模型，主要分为两部分：图的邻接关系以及聚类结果

你可能感兴趣的:(论文阅读,聚类,深度学习)

【LLM】大语言模型（LLMs）林九生人工智能语言模型人工智能自然语言处理
大型语言模型（LLMs）1.什么是大型语言模型？大型语言模型（LargeLanguageModel，LLM）是基于深度学习的自然语言处理模型，能够理解和生成自然语言文本。它们通过在大规模文本数据上进行训练，学习语言的语法、语义和各种语言特征，从而可以执行诸如文本生成、翻译、总结、问答等多种语言任务。以下是大型语言模型的定义和基本原理：1.1定义大型语言模型是由大量参数组成的神经网络，这些参数通过在
【Python】已解决：ModuleNotFoundError: No module named ‘sklearn‘ 屿小夏 python sklearn 人工智能
个人简介：某不知名博主，致力于全栈领域的优质博客分享|用最优质的内容带来最舒适的阅读体验！文末获取免费IT学习资料！文末获取更多信息精彩专栏推荐订阅收藏专栏系列直达链接相关介绍书籍分享点我跳转书籍作为获取知识的重要途径，对于IT从业者来说更是不可或缺的资源。不定期更新IT图书，并在评论区抽取随机粉丝，书籍免费包邮到家AI前沿点我跳转探讨人工智能技术领域的最新发展和创新，涵盖机器学习、深度学习、自然
如何快速在Windows 10 + Anaconda 3 中使用Mxnet及gluon qianchess mxnet使用 mxnet win10 anaconda gluon 人工智能
如何快速在Windows10+Anaconda3中使用Mxnet及gluon网络上Mxnet的安装以及使用方法很多，自从其作者之一李沐推出了基于Mxnet的深度学习课程之后，我也尝试着去使用了一下Mxnet。首先第一步就是在自己的系统中安装Mxnet及其相关组建。现在的Mxnet常常会跟其虚拟环境Gluon结合在一起，所以下文就一起阐述一下，顺便记录一下自己踩的坑。注意本文的大部分内容都可以在官网
3D UNet和Swin-UNETR 学無芷境计算机视觉
3DUNet和Swin-UNETR都是用于医学图像分析的深度学习网络，它们对三维（3D）数据进行特征提取和分割。3DUNet3DUNet是UNet架构的一个变体，专门设计用于处理三维医学图像数据。UNet最初是为二维（2D）图像分割任务设计的，具有典型的编码器-解码器结构。3DUNet扩展了这种架构，以便更好地处理具有深度信息的体积数据，如CT或MRI扫描。主要特点：编码器：逐渐下采样图像，提取并
推荐3D UNet实现：深度学习3D体素数据语义分割的利器！滑辰煦Marc
推荐3DUNet实现：深度学习3D体素数据语义分割的利器！去发现同类优质开源项目:https://gitcode.com/在这个快速发展的深度学习时代，3DUNet已经成为3D图像处理领域中不可或缺的工具，尤其在医疗影像分析和3D物体识别等任务上展现出强大的潜力。这个开源项目为我们提供了一个高效、灵活的3DUNet实现，支持Tensorflow、PyTorch和Chainer三种主流深度学习框架。
锐捷路由器网关RG-NBR6135-E和锐捷交换机 Ruijie Reyee RG-ES224GC 电脑登录web方法 zh7314 硬件工程
2025年1月17日22:29:35最近淘了点东西，准备在家里搞一套深度学习的服务器，先把网关和交换机搞到了锐捷路由器网关RG-NBR6135-E电脑登录web方法在拿到机器的时候，如果不是全新建议拿根牙签，差入reset5-10秒,灯光会全部闪几下，重置机器，因为有些机器会配置的ip和网段无法访问默认的web服务ip，在机器上面的默认配置单配置参考：https://baijiahao.baidu
PyTorch机器学习与深度学习技术方法 Teacher.chenchong 机器学习 python 开发语言
近年来，随着AlphaGo、无人驾驶汽车、医学影像智慧辅助诊疗、ImageNet竞赛等热点事件的发生，人工智能迎来了新一轮的发展浪潮。尤其是深度学习技术，在许多行业都取得了颠覆性的成果。另外，近年来，Pytorch深度学习框架受到越来越多科研人员的关注和喜爱。Python基础知识串讲1、Python环境搭建（Python软件下载、安装与版本选择；PyCharm下载、安装；Python之HelloW
深度学习模块C2f代码详解你是狒狒吗目标检测人工智能计算机视觉 pytorch YOLO 神经网络
C2f是一个用于构建卷积神经网络（CNN）的模块，特别是在YOLOv5和YOLOv8等目标检测模型中。这个模块是一个改进的CSP（CrossStagePartial）Bottleneck结构，旨在提高计算效率和特征提取能力。下面是对C2f类的详细解释：类定义和初始化Python复制classC2f(nn.Module):“”“FasterImplementationofCSPBottleneckw
华为 Ascend 平台 YOLOv5 目标检测推理教程 Lunar* 目标检测华为 YOLO 目标检测
1.背景介绍随着人工智能技术的快速发展，目标检测在智能安防、自动驾驶、工业检测等领域中扮演了重要角色。YOLOv5是一种高效的目标检测模型，凭借其速度和精度的平衡广受欢迎。华为Ascend推理框架（ACL）是AscendCANN软件栈的核心组件，专为AscendAI加速硬件（如Atlas300I）设计，可实现高性能的深度学习推理。在本文中，我们将介绍如何基于华为AscendACL推理框架对YOLO
机器学习和深度学习的概念你好呀我是裤裤深度学习笔记机器学习深度学习人工智能
MachineLearning机器学习，可以看作是找一个函数。这个函数是人类找不到的，所以交给机器来找。DifferenttypesofFunctions**Regression：**函数的输出是一个数值forexample：**Classification：**给出选项，让机器去选择。forexample：检测一个邮件是不是垃圾文件，就可以通过这个来做。选项是两个：垃圾文件or非垃圾文件。下面，
Pytorch实现：LSTM-火灾温度预测骑猪玩狗 pytorch lstm 人工智能
本文为365天深度学习训练营中的学习记录博客原作者：K同学啊前期工作语言环境：Python3.9.18编译器：JupyterLab深度学习环境：Pytorch1.12.11.设置GPUimporttorchimporttorch.nnasnnimporttorchvisionfromtorchvisionimporttransforms,datasetsimportos,PIL,pathlibde
深度学习项目--基于LSTM的火灾预测研究(pytorch实现) 羊小猪~~ RNN LSTM神经网络案例机器学习/数据分析案例深度学习 lstm pytorch 人工智能机器学习 rnn gru
本文为365天深度学习训练营中的学习记录博客原作者：K同学啊前言LSTM模型一直是一个很经典的模型，这个模型当然也很复杂，一般需要先学习RNN、GRU模型之后再学，GRU、LSTM的模型讲解将在这两天发布更新，其中：深度学习基础–一文搞懂RNN深度学习基础–GRU学习笔记(李沐《动手学习深度学习》)这一篇：是基于LSTM模型火灾预测研究，讲述了如何构建时间数据、模型如何构建、pytorch中LST
每天五分钟深度学习框架pytorch：基于vgg块搭建VGG卷积神经网络每天五分钟玩转人工智能深度学习框架pytorch 深度学习 pytorch cnn VGG 卷积神经网络
本文重点前面我们使用pytorch搭建了vgg块，本文我们使用vgg块搭建卷积神经网络VGG16，我们先来看一下vgg16的模型结构是什么样的：搭建vgg16importtorchfromtorchimportnndefvgg_block(num_convs,in_channels,out_channels):net=[nn.Conv2d(in_channels,out_channels,kern
深度学习 Pytorch 张量（Tensor）的创建和常用方法白白糖深度学习pytorch python 深度学习 pytorch 人工智能
1张量的基本创建及其类型和Numpy中的array一样，张量的本质也是结构化地组织了大量的数据。并且在实际操作中，张量的创建和基本功能也与其非常类似。1.1张量(Tensor)函数创建方法张量的最基本创建方法和Numpy中创建Array的格式一致。#Numpy创建数组importnumpyasnp#导入numpya=np.array([1,2,3])importtorch#首次使用,导入torch
PyTorch 神经协同过滤 (NCF) 推荐系统教程陌北v1 pytorch python NCF 神经协同过滤
目录教程概述1.神经协同过滤模型概述NCF模型的主要组成部分：2.数据加载与预处理3.定义神经协同过滤模型4.训练模型5.模型评估6.推荐物品7.完整示例8.总结在本教程中，我们将使用PyTorch实现一个神经协同过滤（NeuralCollaborativeFiltering，简称NCF）推荐系统。神经协同过滤是一种基于深度学习的推荐系统模型，通过学习用户和物品的嵌入表示来预测用户对物品的评分，进
【大模型LoRa微调】Qwen2.5 Coder 指令微调【代码已开源】 FF-Studio 大语言模型开源
本文需要用到的代码已经放在GitHub的仓库啦，别忘了给仓库点个小心心~~~https://github.com/LFF8888/FF-Studio-Resources第001个文件哦~一、引言：大语言模型与指令微调1.1大语言模型发展简史随着深度学习的飞速发展，特别是Transformer架构在自然语言处理（NLP）领域的成功，大语言模型（LLM,LargeLanguageModel）成为近年来
PenGymy论文阅读亚里士多没有德775 论文阅读
这里发现idea被人家先发了，没办法，资料收集的不够全面，现在来学习一下这个项目这篇论文的贡献如下：总的来说，他的主要工作是构建逼真的仿真环境，然后根据这个仿真环境生成真实的靶场，使得这个智能体能够在这个真实的环境去互动。下面来逐渐解析他的工作，我尽量详细一点1、背景和动机这种项目是在网络攻防中，攻防双方攻击者处于暗面，防御者处于明面，这时候受到攻击后应急处理多少会造成损失，那么要是可以提前预测攻
10 个免费的 AI 图片生成工具分享程序员
原文：https://openaigptguide.com/ai-picture-generator/在人工智能（AI）图像生成技术的推动下，各类AI图片生成网站如雨后春笋般涌现，为我们的日常生活提供了丰富多彩的视觉体验。AI图片生成技术原理人工智能（AI）图片生成技术原理是通过计算机程序使用深度学习算法从大量的数据中学习特征，并根据特征创建新的图片。该技术可以模拟人类的绘画过程，学习输入图像的潜
假新闻检测论文（24）A comprehensive survey of multimodal fake news detection techniques... weixin_41964296 假新闻检测自然语言处理
本文综述了利用深度学习架构和注意力机制进行假新闻检测的最新和全面的研究一介绍假新闻定义：虚假或误导性新闻，或“假新闻”，是任何捏造或故意欺骗的媒体内容。假新闻危害：它可以被利用来操纵公众情绪，传播错误信息，甚至干预政治选举。它的主要目的是扭曲、欺骗或操纵个人的信仰和观点。假新闻的形式（类型）：虚假信息在媒体上传播的形式多种多样，包括讽刺、谣言、点击诱饵、错误信息等。讽刺作品通常充满幽默，用来强调特
YOLOv8重磅升级：引入DenseOne密集网络革新主干设计，重塑YOLO目标检测性能新高度程序员杨弋 YOLO 目标检测人工智能
随着深度学习技术的不断进步，目标检测作为计算机视觉领域的重要任务之一，其性能和应用范围也在不断扩大。作为目标检测领域的佼佼者，YOLO（YouOnlyLookOnce）系列算法以其出色的性能和实时性受到了广泛关注。而最近提出的YOLOv8更是在前代版本的基础上进行了多项优化，进一步提升了检测精度和速度。然而，尽管YOLOv8已经取得了显著的进步，但在处理复杂场景和遮挡问题时，仍然存在一定的挑战。为
深度学习驱动的极端天气预测：时空数据异常检测与应用全解析（基于Python + TensorFlow） AI_DL_CODE 深度学习 python tensorflow 人工智能天气预测
摘要：时空数据异常检测在气象领域识别偏离正常模式的数据点，对极端天气预测至关重要。深度学习，尤其是LSTM网络，因其强大的特征学习能力在该领域显示出巨大潜力。通过整合多源气象数据，深度学习模型能够自动挖掘复杂模式和非线性关系，提高预测准确性。然而，挑战依然存在，包括数据质量问题、模型可解释性不足以及极端天气的内在复杂性和不确定性。未来，通过模型架构创新、训练算法优化以及探索深度学习在气候预测、气象
基于深度学习的人脸表情识别系统：YOLOv5 + YOLOv8 + YOLOv10 + UI界面 + 数据集 2025年数学建模美赛深度学习 YOLO ui 分类人工智能
引言随着人工智能的飞速发展，深度学习技术已广泛应用于各个领域，尤其是在计算机视觉领域。人脸识别和表情识别是其中的一个重要应用，能够在多种场景下提供重要的信息，例如安全监控、情感分析、智能客服、健康监测等。在人脸表情识别任务中，准确识别人脸的情感状态（如高兴、愤怒、悲伤等）是一个极具挑战性的任务。随着YOLO系列算法的不断进步，YOLOv5、YOLOv8和YOLOv10的推出大大提高了目标检测的精度
基于YOLOv8深度学习的人脸年龄检测识别系统 2025年数学建模美赛 YOLO 深度学习人工智能 ui 数据挖掘分类
引言随着人工智能和计算机视觉的飞速发展，人脸分析技术在年龄检测领域取得了显著进展。人脸年龄检测系统在安全监控、广告推荐、健康监测等领域有广泛应用。本文将基于YOLOv8目标检测模型和UI界面，开发一个完整的人脸年龄检测识别系统。我们将详细介绍项目的技术实现、数据集构建、模型训练以及UI设计，并附上完整代码。目录引言系统架构设计数据准备公开人脸年龄数据集数据标注格式数据目录结构模型训练YOLOv8环
基于深度学习的人脸表情识别系统（YOLOv10+UI界面+数据集） 2025年数学建模美赛深度学习 YOLO ui 计算机视觉人工智能目标跟踪
在本篇博客中，我们将详细介绍如何构建一个基于深度学习的人脸表情识别系统。该系统主要由三部分组成：YOLOv10（深度学习模型）进行表情识别、UI界面展示识别结果以及数据集的准备和训练过程。我们将从系统架构、数据准备、模型训练、UI设计等多个方面进行全面讲解，最终实现一个能够实时识别并展示人脸表情的系统。目录1.系统架构2.数据集准备2.1FER2013数据集2.2数据预处理3.YOLOv10模型概
基于深度学习的人脸表情识别系统：YOLOv8 + UI界面 + 数据集完整实现 2025年数学建模美赛深度学习 YOLO ui 人工智能代码
1.引言近年来，人脸表情识别在情感计算、智能人机交互、心理学研究等领域有着广泛的应用。深度学习的快速发展，使得高效、准确的人脸表情识别成为可能。通过利用卷积神经网络（CNN）和目标检测技术，可以实现实时、精准的人脸表情识别。本文将基于YOLOv8构建一个完整的人脸表情识别系统。系统集成了数据集准备、YOLOv8模型训练、实时推理以及基于PyQt5的图形用户界面（UI）。通过本文，你将学习如何实现一
【机器学习】聚类【Ⅰ】基础知识与距离度量不牌不改【机器学习】聚类机器学习算法
主要来自周志华《机器学习》一书，数学推导主要来自简书博主“形式运算”的原创博客，包含自己的理解。有任何的书写错误、排版错误、概念错误等，希望大家包含指正。由于字数限制，分成五篇博客。【机器学习】聚类【Ⅰ】基础知识与距离度量【机器学习】聚类【Ⅱ】原型聚类经典算法【机器学习】聚类【Ⅲ】高斯混合模型讲解【机器学习】聚类【Ⅳ】高斯混合模型数学推导【机器学习】聚类【Ⅴ】密度聚类与层次聚类聚类1聚类任务在“无
AI大模型应用架构（ALLMA）白皮书解读百度_开发者中心人工智能大模型数据库自然语言处理
随着人工智能技术的不断发展，AI大模型成为推动生产、生活方式变革，助推产业智能化转型升级，驱动数字经济高质量发展等社会经济发展方面的新引擎。为了全面展示AI大模型的发展全貌，为各界提供新思路，本文将对AI大模型应用架构（ALLMA）白皮书进行解读。一、AI大模型应用架构（ALLMA）的内涵AI大模型应用架构（ALLMA）是一种基于深度学习的人工智能应用架构，旨在通过大规模无标注数据预训练、指令微调
Web APP 阶段性综述预测模型的开发与应用研究 APP construction web app
WebAPP阶段性综述当前，WebAPP主要应用于电脑端，常被用于部署数据分析、机器学习及深度学习等高算力需求的任务。在医学与生物信息学领域，WebAPP扮演着重要角色。在生物信息学领域，诸多工具以WebAPP的形式呈现，相较之下，医学领域的此类应用数量相对较少。在医学和生物信息学的学术论文中，WebAPP是展示研究成果的有效工具，并且还能部署到网络上，服务于实际应用场景。ShinyAPP平台特性
气象海洋水文领域Python机器学习及深度学习实践应用能力提升 AAIshangyanxiu 农林生态遥感编程算法统计语言大气科学 python 机器学习深度学习
Python是功能强大、免费、开源，实现面向对象的编程语言，能够在不同操作系统和平台使用，简洁的语法和解释性语言使其成为理想的脚本语言。除了标准库，还有丰富的第三方库，Python在数据处理、科学计算、数学建模、数据挖掘和数据可视化方面具备优异的性能。上述优势使得Python在气象、海洋、地理、气候、水文和生态等地学领域的科研和工程项目中得到广泛应用。可以预见未来Python将成为气象、海洋和水文
【昇思25天学习打卡营打卡指南-第一天】基本介绍与快速入门 JeffDingAI MindSpore 学习
昇思MindSpore介绍昇思MindSpore是一个全场景深度学习框架，旨在实现易开发、高效执行、全场景统一部署三大目标。其中，易开发表现为API友好、调试难度低；高效执行包括计算效率、数据预处理效率和分布式训练效率；全场景则指框架同时支持云、边缘以及端侧场景。昇思MindSpore总体架构如下图所示：ModelZoo（模型库）：ModelZoo提供可用的深度学习算法网络，也欢迎更多开发者贡献新
辗转相处求最大公约数沐刃青蛟 C++漏洞
无言面对”江东父老“了，接触编程一年了，今天发现还不会辗转相除法求最大公约数。惭愧惭愧！为此，总结一下以方便日后忘了好查找。 1.输入要比较的两个数a,b 忽略：2.比较大小（因为后面要的是大的数对小的数做%操作） 3.辗转相除（用循环不停的取余，如a%b,直至b=0） 4.最后的a为两数的最大公约数 &
F5负载均衡会话保持技术及原理技术白皮书 bijian1013 F5 负载均衡
一.什么是会话保持？在大多数电子商务的应用系统或者需要进行用户身份认证的在线系统中，一个客户与服务器经常经过好几次的交互过程才能完成一笔交易或者是一个请求的完成。由于这几次交互过程是密切相关的，服务器在进行这些交互过程的某一个交互步骤时，往往需要了解上一次交互过程的处理结果，或者上几步的交互过程结果，服务器进行下
Object.equals方法：重载还是覆盖 Cwind java generics override overload
本文译自StackOverflow上对此问题的讨论。原问题链接在阅读Joshua Bloch的《Effective Java（第二版）》第8条“覆盖equals时请遵守通用约定”时对如下论述有疑问： “不要将equals声明中的Object对象替换为其他的类型。程序员编写出下面这样的equals方法并不鲜见，这会使程序员花上数个小时都搞不清它为什么不能正常工作：” pu
初始线程 15700786134
暑假学习的第一课是讲线程，任务是是界面上的一条线运动起来。既然是在界面上，那必定得先有一个界面，所以第一步就是，自己的类继承JAVA中的JFrame，在新建的类中写一个界面，代码如下： public class ShapeFr
Linux的tcpdump 被触发 tcpdump
用简单的话来定义tcpdump，就是：dump the traffic on a network，根据使用者的定义对网络上的数据包进行截获的包分析工具。 tcpdump可以将网络中传送的数据包的“头”完全截获下来提供分析。它支持针对网络层、协议、主机、网络或端口的过滤，并提供and、or、not等逻辑语句来帮助你去掉无用的信息。实用命令实例默认启动 tcpdump 普通情况下，直
安卓程序listview优化后还是卡顿肆无忌惮_ ListView
最近用eclipse开发一个安卓app，listview使用baseadapter，里面有一个ImageView和两个TextView。使用了Holder内部类进行优化了还是很卡顿。后来发现是图片资源的问题。把一张分辨率高的图片放在了drawable-mdpi文件夹下，当我在每个item中显示，他都要进行缩放，导致很卡顿。解决办法是把这个高分辨率图片放到drawable-xxhdpi下。 &nb
扩展easyUI tab控件，添加加载遮罩效果知了ing jquery
(function () { $.extend($.fn.tabs.methods, { //显示遮罩 loading: function (jq, msg) { return jq.each(function () { var panel = $(this).tabs(&
gradle上传jar到nexus 矮蛋蛋 gradle
原文地址： https://docs.gradle.org/current/userguide/maven_plugin.html configurations { deployerJars } dependencies { deployerJars "org.apache.maven.wagon
千万条数据外网导入数据库的解决方案。 alleni123 sql mysql
从某网上爬了数千万的数据，存在文本中。然后要导入mysql数据库。悲剧的是数据库和我存数据的服务器不在一个内网里面。。 ping了一下， 19ms的延迟。于是下面的代码是没用的。 ps = con.prepareStatement(sql); ps.setString(1, info.getYear())............; ps.exec
JAVA IO InputStreamReader和OutputStreamReader 百合不是茶 JAVA.io操作字符流
这是第三篇关于java.io的文章了，从开始对io的不了解-->熟悉--->模糊，是这几天来对文件操作中最大的感受，本来自己认为的熟悉了的，刚刚在回想起前面学的好像又不是很清晰了，模糊对我现在或许是最好的鼓励我会更加的去学加油！： JAVA的API提供了另外一种数据保存途径，使用字符流来保存的，字符流只能保存字符形式的流字节流和字符的难点：a,怎么将读到的数据
MO、MT解读 bijian1013 GSM
MO= Mobile originate，上行，即用户上发给SP的信息。MT= Mobile Terminate，下行，即SP端下发给用户的信息；上行:mo提交短信到短信中心下行:mt短信中心向特定的用户转发短信，你的短信是这样的，你所提交的短信，投递的地址是短信中心。短信中心收到你的短信后，存储转发，转发的时候就会根据你填写的接收方号码寻找路由，下发。在彩信领域是一样的道理。下行业务：由SP
五个JavaScript基础问题 bijian1013 JavaScript call apply this Hoisting
下面是五个关于前端相关的基础问题，但却很能体现JavaScript的基本功底。问题1：Scope作用范围考虑下面的代码： (function() { var a = b = 5; })(); console.log(b); 什么会被打印在控制台上？回答：上面的代码会打印 5。 &nbs
【Thrift二】Thrift Hello World bit1129 Hello world
本篇，不考虑细节问题和为什么，先照葫芦画瓢写一个Thrift版本的Hello World，了解Thrift RPC服务开发的基本流程 1. 在Intellij中创建一个Maven模块，加入对Thrift的依赖，同时还要加上slf4j依赖，如果不加slf4j依赖，在后面启动Thrift Server时会报错 <dependency>
【Avro一】Avro入门 bit1129 入门
本文的目的主要是总结下基于Avro Schema代码生成，然后进行序列化和反序列化开发的基本流程。需要指出的是，Avro并不要求一定得根据Schema文件生成代码，这对于动态类型语言很有用。 1. 添加Maven依赖 <?xml version="1.0" encoding="UTF-8"?> <proj
安装nginx+ngx_lua支持WAF防护功能 ronin47
需要的软件:LuaJIT-2.0.0.tar.gz nginx-1.4.4.tar.gz &nb
java-5.查找最小的K个元素-使用最大堆 bylijinnan java
import java.util.Arrays; import java.util.Random; public class MinKElement { /** * 5.最小的K个元素 * I would like to use MaxHeap. * using QuickSort is also OK */ public static void
TCP的TIME-WAIT bylijinnan socket
原文连接： http://vincent.bernat.im/en/blog/2014-tcp-time-wait-state-linux.html 以下为对原文的阅读笔记说明：主动关闭的一方称为local end，被动关闭的一方称为remote end 本地IP、本地端口、远端IP、远端端口这一“四元组”称为quadruplet，也称为socket 1、TIME_WA
jquery ajax 序列化表单 coder_xpf Jquery ajax 序列化
checkbox 如果不设定值，默认选中值为on；设定值之后，选中则为设定的值 <input type="checkbox" name="favor" id="favor" checked="checked"/> $("#favor&quo
Apache集群乱码和最高并发控制 cuisuqiang apache tomcat 并发集群乱码
都知道如果使用Http访问，那么在Connector中增加URIEncoding即可，其实使用AJP时也一样，增加useBodyEncodingForURI和URIEncoding即可。最大连接数也是一样的，增加maxThreads属性即可，如下，配置如下： <Connector maxThreads="300" port="8019" prot
websocket dalan_123 websocket
一、低延迟的客户端-服务器和服务器-客户端的连接很多时候所谓的http的请求、响应的模式，都是客户端加载一个网页，直到用户在进行下一次点击的时候，什么都不会发生。并且所有的http的通信都是客户端控制的，这时候就需要用户的互动或定期轮训的，以便从服务器端加载新的数据。通常采用的技术比如推送和comet（使用http长连接、无需安装浏览器安装插件的两种方式：基于ajax的长
菜鸟分析网络执法官 dcj3sjt126com 网络
最近在论坛上看到很多贴子在讨论网络执法官的问题。菜鸟我正好知道这回事情.人道"人之患好为人师" 手里忍不住,就写点东西吧. 我也很忙.又没有MM,又没有MONEY....晕倒有点跑题. OK,闲话少说,切如正题. 要了解网络执法官的原理. 就要先了解局域网的通信的原理. 前面我们看到了.在以太网上传输的都是具有以太网头的数据包.
Android相对布局属性全集 dcj3sjt126com android
RelativeLayout布局android:layout_marginTop="25dip" //顶部距离android:gravity="left" //空间布局位置android:layout_marginLeft="15dip //距离左边距 // 相对于给定ID控件android:layout_above 将该控件的底部置于给定ID的
Tomcat内存设置详解 eksliang jvm tomcat tomcat内存设置
Java内存溢出详解一、常见的Java内存溢出有以下三种： 1. java.lang.OutOfMemoryError: Java heap space ----JVM Heap（堆）溢出JVM在启动的时候会自动设置JVM Heap的值，其初始空间(即-Xms)是物理内存的1/64，最大空间(-Xmx)不可超过物理内存。可以利用JVM提
Java6 JVM参数选项 greatwqs java HotSpot jvm jvm参数 JVM Options
Java 6 JVM参数选项大全（中文版）作者：Ken Wu Email: [email protected] 转载本文档请注明原文链接 http://kenwublog.com/docs/java6-jvm-options-chinese-edition.htm！本文是基于最新的SUN官方文档Java SE 6 Hotspot VM Opt
weblogic创建JMC i5land weblogic jms
进入 weblogic控制太 1.创建持久化存储 --Services--Persistant Stores--new--Create FileStores--name随便起--target默认--Directory写入在本机建立的文件夹的路径--ok 2.创建JMS服务器 --Services--Messaging--JMS Servers--new--name随便起--Pers
基于 DHT 网络的磁力链接和BT种子的搜索引擎架构 justjavac DHT
上周开发了一个磁力链接和 BT 种子的搜索引擎 {Magnet & Torrent}，本文简单介绍一下主要的系统功能和用到的技术。系统包括几个独立的部分：使用 Python 的 Scrapy 框架开发的网络爬虫，用来爬取磁力链接和种子；使用 PHP CI 框架开发的简易网站；搜索引擎目前直接使用的 MySQL，将来可以考虑使
sql添加、删除表中的列 macroli sql
添加没有默认值：alter table Test add BazaarType char(1) 有默认值的添加列：alter table Test add BazaarType char(1) default(0) 删除没有默认值的列：alter table Test drop COLUMN BazaarType 删除有默认值的列：先删除约束（默认值）alter table Test DRO
PHP中二维数组的排序方法 abc123456789cba 排序二维数组 PHP
<?php/*** @package BugFree* @version $Id: FunctionsMain.inc.php,v 1.32 2005/09/24 11:38:37 wwccss Exp $*** Sort an two-dimension array by some level
hive优化之------控制hive任务中的map数和reduce数 superlxw1234 hive hive优化
一、控制hive任务中的map数: 1. 通常情况下，作业会通过input的目录产生一个或者多个map任务。主要的决定因素有： input的文件总个数，input的文件大小，集群设置的文件块大小(目前为128M, 可在hive中通过set dfs.block.size;命令查看到，该参数不能自定义修改)；2.
Spring Boot 1.2.4 发布 wiselyman spring boot
Spring Boot 1.2.4已于6.4日发布，repo.spring.io and Maven Central可以下载(推荐使用maven或者gradle构建下载)。这是一个维护版本，包含了一些修复small number of fixes,建议所有的用户升级。 Spring Boot 1.3的第一个里程碑版本将在几天后发布，包含许多

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他