函数空间简介
最近因为项目需要用到再生核希尔伯特空间的知识,看了网上很多资料,写的都很不错,现自己将有关数学上空间的知识进行整理。
首推一个上海交通大学老师讲的函数空间一课,通俗易懂。其余的一些参考文章会在文末给出。
现代数学的一个特点就是以集合为研究对象,这样的好处就是可以将很多不同问题的本质抽象出来,变成同一个问题,当然这样的坏处就是描述起来比较抽象,很多人就难以理解了。
从数学的本质来看,最基本的集合有两类:线性空间(有线性结构的集合)、度量空间(有度量结构的集合)。
函数空间
- 距离
- 线性空间(向量空间)
- 赋范向量空间(范数向量空间)
- 内积空间
- 欧几里得空间
- 巴拿赫空间
- 希尔伯特空间(HS)
-
- 核函数
- 再生核希尔伯特空间(RKHS)
- 拓扑空间
- 总结
- 参考资料
距离
一切空间都要从距离这个词开始:我们通过对距离的抽象,得出距离最一般的定义:
设 X X X是一非空集合,任给一对这一集合的元素 x , y x,y x,y,都给定一个实数 d ( x , y ) d(x,y) d(x,y)与它们对应,并满足:
- d ( x , y ) ≥ 0 d(x,y)\ge 0 d(x,y)≥0
- d ( x , y ) = 0 ⇔ x = y d(x,y)=0 \Leftrightarrow x=y d(x,y)=0⇔x=y
- d ( x , y ) = d ( y , x ) d(x,y)=d(y,x) d(x,y)=d(y,x)
- d ( x , y ) ≤ d ( x , z ) + d ( z , y ) d(x,y)\leq d(x,z)+d(z,y) d(x,y)≤d(x,z)+d(z,y)
则称 d ( x , y ) d(x,y) d(x,y)为 x , y x,y x,y两元素间的距离。
Note:
上面是抽象的定义,距离可以分好多种,比如我们常见的:向量之间的距离、函数之间的距离、超市与家之间的距离等。
线性空间(向量空间)
线性结构:满足向量加法、数乘、加法交换律、结合律、零元、负元、数乘的交换律、单位一、数乘与加法的结合律。
线性空间:
集合中的元素是向量,这些向量满足线性结构,这样的集合就是线性空间。
Note:
- 因为有数乘和加法,所以空间中可以找到一组基底(坐标系),能够通过线性组合得到空间中所有的点。对于一个线性空间来说,只要知道其基即可,集合中的元素只要知道其在给定基下的坐标即可。
- 线性空间又叫向量空间,两个是一个意思。
- 这个线性是线性代数里的线性,是线性相关、线性无关的线性,不是线性函数的线性。
- 我们在一些参考文章终会看到:“一个由函数组成的向量空间”。我是这么理解的:首先由函数作为元素组成的空间是函数空间,向量空间是函数空间的一种。其次,我们都将函数看成向量,那么线性空间中的每一个元素(函数),都可以看成空间中基的线性组合。比如在再生核希尔伯特空间中,每一个函数(向量)都可以看成是正交基 { λ i ψ i } i = 1 ∞ \{\sqrt{\lambda_i}\psi_i\}_{i=1}^\infty {λiψi}i=1∞的线性组合(再生核希尔伯特空间也是线性空间的一种,它是由这组正交基构成的希尔伯特空间 H \mathcal{H} H)。
赋范向量空间(范数向量空间)
线性空间中的元素没有“长度”(可以狭义地理解为空间中线段的长度),为了量化线性空间中的元素,所以又在线性空间引入特殊的“长度”,即范数。赋予了范数的线性空间即称为赋范向量空间。
首先给出范数的定义:
设 ∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣是 R + R^+ R+的范数,其满足:
- 非负性 ∣ ∣ x ∣ ∣ ≥ 0 ||x||\ge0 ∣∣x∣∣≥0。
- 对 ∀ x ∈ R + , ∣ ∣ x ∣ ∣ = 0 ⇔ x = 0 \forall x\in R^+,||x||=0 \Leftrightarrow x=0 ∀x∈R+,∣∣x∣∣=0⇔x=0。
- 对 ∀ α ∈ R , x ∈ R + \forall \alpha\in R,x\in R^+ ∀α∈R,x∈R+, ∣ ∣ α x ∣ ∣ = ∣ α ∣ ∗ ∣ ∣ x ∣ ∣ ||\alpha x|| = |\alpha|*||x|| ∣∣αx∣∣=∣α∣∗∣∣x∣∣
- 对 ∀ x , y ∈ R + \forall x,y\in R^+ ∀x,y∈R+, ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y||\leq ||x|| + ||y|| ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣
可以看出范数的定义比距离要多出第③条,因此范数是"强化"了的距离。
两者关系: ∣ ∣ x ∣ ∣ = d ( x , 0 ) ||x|| = d(x, 0) ∣∣x∣∣=d(x,0)
范数分为向量范数和矩阵范数,有关范数点击这里。
Note:
- 赋予范数、距离的集合分别称为赋范空间和度量空间。
- 若在其上再加上线性结构称为线性赋范空间和线性度量空间。
内积空间
赋范线性空间中两个元素之间没有角度的概念,为了解决该问题,所以在线性空间中又引入了内积的概念。
内积的定义:
设 ⟨ x , y ⟩ ∈ R \langle x,y\rangle\in R ⟨x,y⟩∈R,且满足:
- 对称性。
- 对第一变元的线性性: ⟨ a x , y ⟩ = a ⟨ x , y ⟩ ; ⟨ x + z , y ⟩ = ⟨ x , y ⟩ + ⟨ z , y ⟩ \langle ax,y\rangle=a\langle x,y\rangle;\langle x+z,y\rangle=\langle x,y\rangle+\langle z,y\rangle ⟨ax,y⟩=a⟨x,y⟩;⟨x+z,y⟩=⟨x,y⟩+⟨z,y⟩
- 正定性。
内积与范数的关系: ⟨ x , x ⟩ = ∣ ∣ x ∣ ∣ 2 \langle x,x\rangle = ||x||^2 ⟨x,x⟩=∣∣x∣∣2。另外内积是范数的加强版,因为内积还包含了向量角度的概念。因此内积可以定义范数,但范数不可以定义内积。
Note:
- 内积空间是在线性空间上定义内积的空间,其自带线性结构。
- 内积空间也属于赋范线性空间。
欧几里得空间
内积可在空间中建立欧几里得几何学,例如交角、垂直和投影等,故习惯上称其为欧几里得空间。
欧几里得空间(甚至简称 n 维空间)或有限维实内积空间。
欧里几何空间可以说是内积空间的引申。
巴拿赫空间
提出希尔伯特空间之后,1922年巴拿赫提出了巴拿赫空间,指的是完备的赋范空间。
Note:
巴拿赫空间不包含角度。
希尔伯特空间(HS)
基本的线性空间只包括加法和数乘操作,在此基础上我们引入内积操作,这样就把空间升级为内积空间。根据内积我们可以定义一个范数: ∣ ∣ x ∣ ∣ = ⟨ x , x ⟩ ||x||=\langle x,x\rangle ∣∣x∣∣=⟨x,x⟩,于是我们就得到了一个赋范向量空间。有了范数之后我们就可以引入一个度量: d ( x , y ) = ∣ ∣ x − y ∣ ∣ d(x,y)=||x-y|| d(x,y)=∣∣x−y∣∣用于计算向量 x 和 y x和y x和y之间的距离。于是我们就得到一个度量空间。如果这样的空间在这个度量下是完备的,那么这个空间叫做希尔伯特空间。
也就是说:希尔伯特空间就是完备的内积空间。完备性就是说这个空间必须是个完备空间,完备空间指在一个度量空间内的柯西序列都收敛于该空间内的一个元素,不跑出这个空间。(参考:完备性与希尔伯特空间)
Note:
再生核希尔伯特空间是希尔伯特空间的一个子类,其需要核函数Kernel,所以我们先了解下核函数。
核函数
个人认为核函数在周志华老师的西瓜书上讲的比较详细了:核函数用 κ \kappa κ表示,本质就是个二元函数,可以看成是无限维矩阵(同理一元函数可以看出无限维向量)。
核函数必须满足2个条件:
- 对称性: κ ( x , y ) = κ ( y , x ) \kappa(x,y)= \kappa(y,x) κ(x,y)=κ(y,x)。
- 正定性: ∬ f ( x ) κ ( x , y ) f ( y ) d x d y ≥ 0 \iint f(x)\kappa(x,y)f(y)\mathrm{d}x\mathrm{d}y \ge0 ∬f(x)κ(x,y)f(y)dxdy≥0。或者核矩阵半正定。
因为核函数是半正定矩阵,所以必定是实对称矩阵,因此可作特征分解,与n维矩阵特征分解类似,可分解得到n个特征值和最多n个特征向量,核函数也可以分解得到无限个特征值和特征函数(特征方程)。



再生核希尔伯特空间(RKHS)
参考
再生核希尔伯特空间与核函数
从线性空间到再生核希尔伯特空间
RKHS是希尔伯特空间的一个子类,在希尔伯特空间引入的核函数又叫可再生核。这里的“再生核”指的是核函数 κ \kappa κ的可再生性,即核函数 κ ( x , y ) \kappa(x,y) κ(x,y)可以创造出2个核函数 κ ( ⋅ , x ) \kappa(\cdot\,,x) κ(⋅,x)和 κ ( ⋅ , y ) \kappa(\cdot\,,y) κ(⋅,y)的内积。
那么这种可再生核与普通的核函数有啥特殊的呢?
——可再生核定义:
在希尔伯特空间中,我们能找到唯一一个核函数,满足:
- 对任意固定 x 0 x_0 x0属于 X X X, κ ( x , x 0 ) \kappa(x,x_0) κ(x,x0)作为 x x x的函数属于希尔伯特空间 H \mathcal{H} H。
- 对任意 x x x属于 X X X, f ( ⋅ ) f(\cdot) f(⋅)属于 H \mathcal{H} H,有 f ( x ) = ⟨ f ( ⋅ ) , κ ( ⋅ , x ) ⟩ H f(x)=\langle f(\cdot),\kappa(\cdot\, ,x)\rangle_\mathcal{H} f(x)=⟨f(⋅),κ(⋅,x)⟩H。
Note:
- 一个希尔伯特空间是一个再生核希尔伯特空间,当且仅当它有一个再生核。
- 对于给定的希尔伯特空间,再生核是唯一的。
- 任何一个核函数都隐式的定义了一个再生核希尔伯特空间。
- 我们使用“
核技巧”把一组数据映射到一个高维空间,这个空间就是一个可再生核希尔伯特空间。
那么这个可再生核有什么用呢?
——当数据映射到高维空间后,可以通过核技巧将内积转为低维空间下的核函数!
推导过程:
法一:
令 f ( ⋅ ) = K ( ⋅ , y ) f(\cdot)=K(\cdot\, ,y) f(⋅)=K(⋅,y),则 f ( x ) = K ( x , y ) = ⟨ K ( ⋅ , y ) , K ( ⋅ , x ) ⟩ f(x)=K(x,y)=\langle K(\cdot\, ,y),K(\cdot\, , x)\rangle f(x)=K(x,y)=⟨K(⋅,y),K(⋅,x)⟩。
设 x x x为低维特征向量, ϕ ( x ) \phi(x) ϕ(x)为映射到高维的特征向量。
定义 ϕ ( x ) = K ( ⋅ , x ) \phi(x)=K(\cdot\, , x) ϕ(x)=K(⋅,x),则 K ( x , y ) = ⟨ ϕ ( y ) , ϕ ( x ) ⟩ K(x,y)=\langle \phi(y),\phi(x)\rangle K(x,y)=⟨ϕ(y),ϕ(x)⟩——这就是核技巧!高维的特征向量内积可以转为低维向量 x , y x,y x,y的核函数。
法二:
再生核希尔伯特空间英文版
拓扑空间
这个空间不是很了解,只是粗略的说个概念:以上的所有空间都是围绕(基于)距离来说的,那有没有不需要距离的空间?有,那就是拓扑空间。拓扑空间是一个不需要内积,不需要距离的空间。
例如:
社交圈的描述、学号的指定是“连续”的。
总结
-
不管什么空间,都是由<
元素,规则>组成的。 -
有了拓扑就是拓扑空间;有了距离就是度量空间;有了范数就是赋范空间,有了内积就是内积空间(已有线性结构)。
-
如果各个空间加上线性结构:拓扑线性空间、线性度量空间、线性赋范空间、内积空间
-
线性赋范空间加上完备性—巴拿赫空间;内积空间加上完备性就是希尔伯特空间。
-
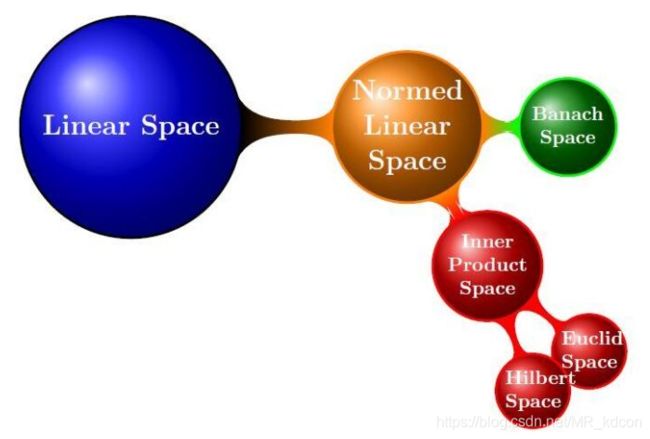
从线性空间-希尔伯特空间,是由比较松的约束条件到比较紧的约束条件。换句话说:拓扑比距离更加宽泛,拓扑是“弱化”了的距离;范数定义了“强化”了的距离;内积是较距离和范数有更多内涵。他们之间的关系如下图所示:
-
线性空间与度量空间是两个不同的概念,没有交集;赋范线性空间就是赋予了范数的线性空间,也是度量空间(具有线性结构的度量空间);内积空间是赋范线性空间;希尔伯特空间就是完备的内积空间。
参考资料
上交函数空间课
函数空间总结
函数空间讲解
再生核希尔伯特空间
如何理解希尔伯特空间-TimXP&qang pan
从线性空间到再生核希尔伯特空间
再生核希尔伯特空间与核函数
希尔伯特空间的完备性
柯西序列
函数空间