逻辑斯蒂回归公式

逻辑斯蒂回归

首先我们要知道逻辑斯蒂回归是干什么用的，它可以用回归的方式找到分类边界曲线

1、sigmoid压缩函数：
$$g(z)=\frac{1}{1+e^{-z}}$$
在该函数中，z大于0，该函数值大于0.5，z<0，该函数值小于0.5，根据z和0.5的关系，可以实现分类。

函数范围（0-1）

例1：
$$h_{\theta }(x)=g({\theta }_0+\theta 1x1+\theta 2x2)$$
$$g(z)=\frac{1}{1+e^{-z}}$$

取
$${\theta }_0=-3,\theta 1=1,\theta 2=1$$
得到分类函数：
$$-3+x1+x2=0$$

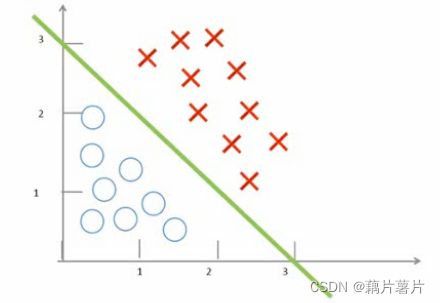
例二：

$$h_{\theta }(x)=g({\theta }_0+\theta 1x_1+\theta 2x_2+\theta 3x_1^2+\theta 4x_2^2)$$
取
$$\theta 0=-1,\theta 1=0,\theta 2=0,\theta 3=1,\theta 4=1$$
得到分类曲线：
$$x_1^2+x_2^2-1=0$$

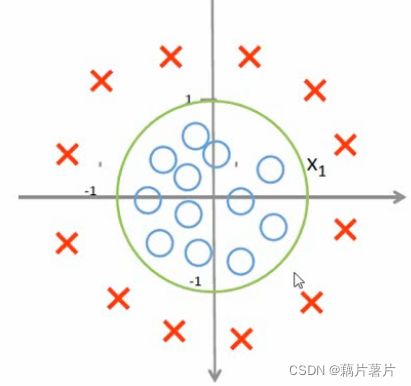
2、损失函数

如果还是用平方损失函数，容易陷入局部极小值，且体现不出来分类正确或错误的奖励或惩罚，所以要构建一个新的损失函数：
$$\begin{gathered} Cost(h_{\theta }(x),y)=-log(h_{\theta }(x)),y=1 \\ -log(1-h_{\theta }(x)),y=0 \end{gathered}$$
画出图像：

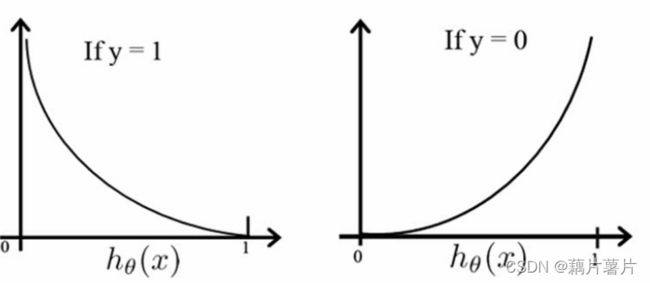
转换成一个公式：
$$Cost(h_{\theta }(x),y)=-\frac{1}{m}\sum _{i=1}^m[y_{i}log(h_{\theta }(x_i))+(1-y_i)log(1-h_{\theta }(x_i))]$$
防止过拟合，加入正则化项：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y_{i}log(h_{\theta }(x_i))+(1-y_i)log(1-h_{\theta }(x_i))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$