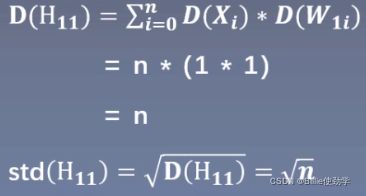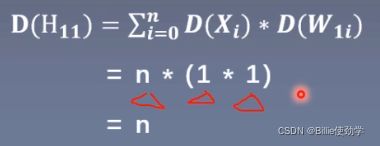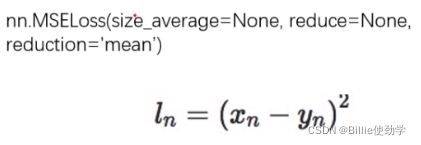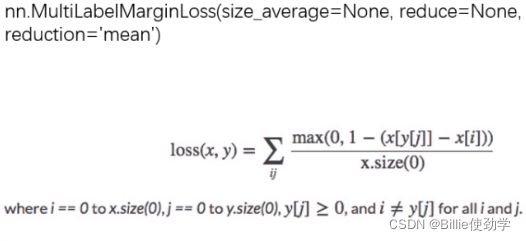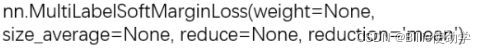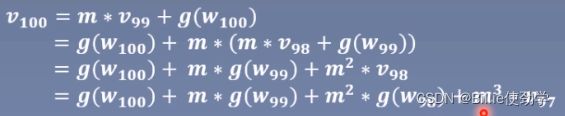Pytorch基础学习（第四章-Pytorch损失优化）

课程一览表：

目录

一、权值初始化

1.梯度消失与爆炸

2.Xavier方法与kaiming方法

3.常用初始化方法

二、损失函数

1.损失函数概念

2.交叉熵损失函数

3.NLLLoss

4.BCE

5.BCEWithLogists Loss

6.nn.L1Loss

7.nn.MSELoss

8.SmoothL1Loss

9.PoissonNLLLoss

10.KLDivergence Loss

11.Margin Ranking Loss

12.Multi Label Margin Loss

13.SoftMargin Loss

14.MultiLabel SoftMargin Loss

15.Multi Margin Loss

16.Triplet Margin Loss

17.Hinge Embedding Loss

18.Cosine Embedding Loss

19.CTC Loss

四、优化器（一）

1.什么是优化器

2.optimizer的属性和方法

五、优化器（二）

1.learning rate 学习率

2.momentum 动量

3.torch.optim.SGD

4.Pytorch的十种优化器

六、学习率调整策略

1.为什么要调整学习率？

2.pytorch的六种学习率调整策略

3.学习率调整小结

---

一、权值初始化

1.梯度消失与爆炸

为避免梯度消失与梯度爆炸的产生，就要严格控制网络输出层的输出值得尺度范围，不要太大、也不要太小。

 根据代码看原理

构建MLP类，init函数中定义了100个网络层，每个网络层有256个神经元

forward进行前向传播

initialize函数对权值进行初始化

如下所示，使用标准正态分布的方法对权值进行初始化

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.normal_(m.weight.data)
             

打印结果：

# flag = 0
flag = 1
if flag:
    layer_nums = 100
    neural_nums = 256
    batch_size = 16

    net = MLP(neural_nums, layer_nums)
    net.initialize()

    inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

    output = net(inputs)
    print(output)

可以看到，输出全为nan，说明数据非常大或者非常小，已经超出了当前精度所表示的范围

 那么，从什么时候开始，数据变成了nan呢？

如下，我们通过标准差来衡量数据的尺度范围

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            # x = torch.relu(x)

            #打印每一层的标准差
            print("layer:{}, std:{}".format(i, x.std()))
            #如果结果为nan，则停止前向传播
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

打印结果：

可以看到，到第31层时，数据已经是nan了，std太大，超出当前数据精度可以表示的范围

 下面通过方差的公式推导来观察，为什么网络层的输出的标准差会越来越大。

三个基本公式：

 由上面可得：

初始化时，我们默认均值为0，即期望为0，标准差为1

 

下面来观察网络层神经元的标准差是怎样的

n为隐藏层神经元个数，第一个1为输入值得方差，第二个1为网络层权值的方差

 

从公式推导可以发现，第一个隐藏层的H1 的输出值得方差变为了n，而输入的数据的方差为1，经过一个网络层的前向传播，数据方差就变为了之前的n倍，标准差扩大了sqrt（n）倍，如果再传入第二个隐藏层，它的标准差就会变为n，经过不断传播，每经过一层，它的输出值数据的尺度范围都会不断的扩大sqrt(n)倍，最终超出精度可表示的范围，引发梯度爆炸。

从以下公式可以看出，如果想让网络层方差保持尺度不变, 那就只能让方差等于1（因为多次相乘结果不变）

即如果想让D(H1) = 1，则D(W)的方差为1/n

下面我们根据这个方法：0均值，sqrt(1/n)标准差的方法进行初始化，并观察输出的标准差

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                # nn.init.normal_(m.weight.data)
                nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))    # normal: mean=0, std=1

输出结果为：

看到每一层的标准差都在1左右

说明采用恰当的权值初始化方法，可以实现多层的全连接网络的输出值得尺度维持在一定的范围之内，不会过大，也不会过小

 以上方法我们未使用到激活函数

下面我们学习一下具有激活函数的权值初始化

下面我们加入激活函数看一下输出结果

此处加入tanh激活函数

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            x = torch.tanh(x)

            #打印每一层的标准差
            print("layer:{}, std:{}".format(i, x.std()))
            #如果结果为nan，则停止前向传播
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

        return x

输出结果：

发现std会变的越来越小，从而导致梯度的消失

2.Xavier方法与kaiming方法

（1）Xavier初始化方法

针对以上具有激活函数的问题，提出了Xavier初始化方法，在文章中，提出了结合方差一致性原则，即让每一个网络层输出值的方差尽量等于1 ，主要针对饱和激活函数，如sigmoid，tanh

通过文章中的公式推导，得到了以下两个等式，ni为输入层的神经元个数，ni+1是输出层的神经元个数，即让权值的方差乘神经元个数等于1。同时考虑了前向传播和反向传播数据尺度问题得到的两个公式，同时结合方差一致性准则，最终得到了权值的方差D(W),如下图所示

 Xavier通常采用均匀分布，下面推导均匀分布的上限和下限，设上限为-a，下限为a

将这两个D(W)相等，得出a，最终得出W的上限和下限

 通过代码看一下：

此处我们手动计算通过均匀分布来初始化

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                #标准正态分布初始化权重
                # nn.init.normal_(m.weight.data)
                # nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))    # normal: mean=0, std=1

                #计算均匀分布的上限、下限
                a = np.sqrt(6 / (self.neural_num + self.neural_num))

                #观察数据输入到激活函数之后，标准差的变化
                tanh_gain = nn.init.calculate_gain('tanh')
                a *= tanh_gain
                #均匀分布初始化权重
                nn.init.uniform_(m.weight.data, -a, a)

输出结果：
std维持在0.65左右，每个网络层的输出数据分布都不会过大或过小

下面我们采用 pytorch的Xavier初始化方法

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                tanh_gain = nn.init.calculate_gain('tanh')
                nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

输出结果：

可以看到输出结果与之前自定义的结果一模一样

（2）kaiming方法

但是由于非饱和函数ReLU的出现，Xavier不再适用。

举个栗子：我们将激活函数改为ReLU，仍然使用Xavier初始化方法

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
            # x = torch.tanh(x)
            x = torch.relu(x)

            #打印每一层的标准差
            print("layer:{}, std:{}".format(i, x.std()))
            #如果结果为nan，则停止前向传播
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

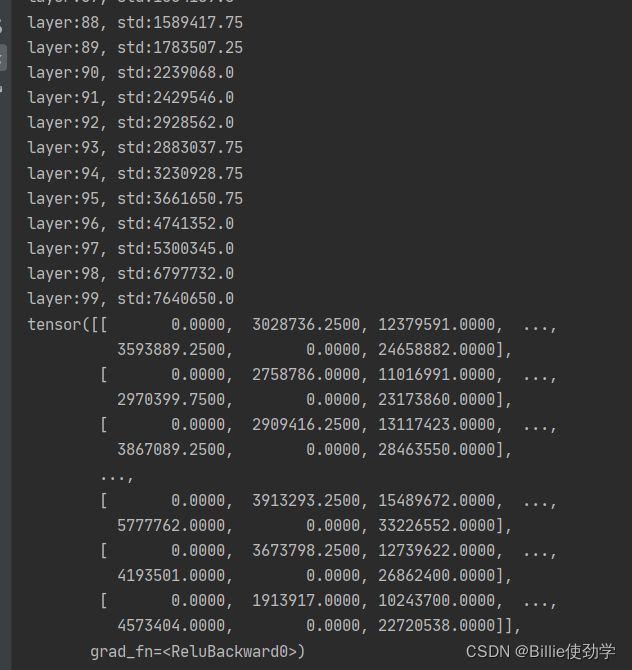
        return x

网络层输出结果：

可以看到方差由开始的1，变成了非常大的一个尺度。

针对ReLU这种非饱和函数，何凯明大神们提出了Kaming初始化方法 。

方差一致性：保持数据尺度维持在恰当范围，通常方差为1

针对的激活函数：ReLU及其变种

通过推导得到方差的公式如下

ni为输入层的神经元个数

 针对ReLU的变种，其方差公式为：

a为负半轴的斜率

当a = 0时，为ReLU激活函数

 则权值的标准差为：

 下面我们根据这个公式来初始化权重

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
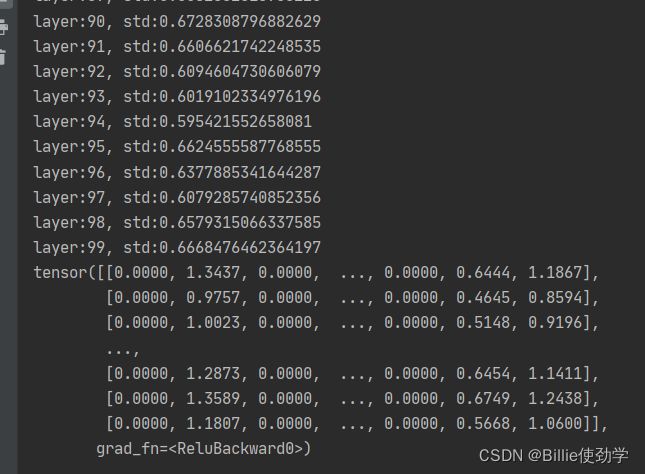
                nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))

输出结果：

网络层标准差维持在0.65左右

 利用pytorch自带的方法初始化权重

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.kaiming_normal_(m.weight.data)

输出结果：

可以看到每层的std与之前手动计算的结果一模一样

3.常用初始化方法

十种初始化方法：

下面学习一个函数：

nn.init.calculate_gain

主要功能：计算激活函数的方差尺度变化

主要参数：

• nonlinearity：激活函数名称
• param：激活函数的参数，如Leaky ReLU的negative_slop

方差变化尺度：输入数据的方差除以经过激活函数之后输出数据的方差

# ======================================= calculate gain =======================================

# flag = 0
flag = 1

if flag:

    x = torch.randn(10000)
    out = torch.tanh(x)

    #手动计算
    gain = x.std() / out.std()
    print('gain:{}'.format(gain))

    #官方给出
    tanh_gain = nn.init.calculate_gain('tanh')
    print('tanh_gain in PyTorch:', tanh_gain)

输出结果：

tanh方差争议在1.6左右

即，对于0均值1标准差的数据x，经过tanh之后，它的标准差会减小1.6倍左右

二、损失函数

1.损失函数概念

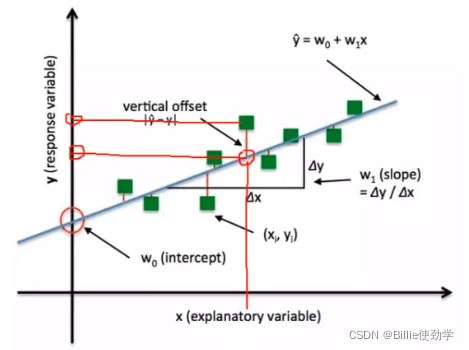
损失函数：衡量模型输出与真实标签的差异

下图可以看到这个之前没有拟合每一个点，故会产生loss

此处计算loss 的方式是，绿方块的y值到预期位置的y值得差的绝对值

 在讨论损失函数时，总是提到下面这三个函数，那么这是哪个函数之间有什么关系呢？

loss function计算一个样本的差异

 

 代价函数计算整个样本集的loss的平均值

 目标函数是最终的目标：代价和约束

代价函数是越小越好吗？

不一定，有时候可能会过拟合

即很好的拟合每一个数据点，所以cost会很小，但这不一定是个好模型

pytorch中的loss

 size_average和reduce这两个参数不需要使用，reduction可以实现其功能

2.交叉熵损失函数

代码调试看nn.CrossEntropyLoss() 的运行原理

进入到CrossEntropyLoss类的forward

 点击进入，来到function的CrossEntropy类，计算loss

 调用完成后，可以看到loss已经计算出来了，loss = 0.7028

nn.CrossEntropyLoss

功能：nn.LogSoftmax()与nn.NULLLoss()结合，进行交叉熵计算

主要参数：

• weight：各类别的loss设置权限
• ignore_index：忽略某个类别
• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

注意：使用nn.LogSoftmax()将概率归一化，应为交叉熵损失函数一般用在分类任务当中，而分类任务通常需要计算两个输出的概率值，所以交叉熵损失函数用来衡量两个概率分布之间的差异，交叉熵值越低，说明两个概率分布越近。

为什么交叉熵越低，说明两个概率分布越近呢？

那就不得不提相对熵和信息熵这两个概念了

下面来学习一下这三个熵之间的关系

熵：用来描述整个概率分布的不确定性，熵越大，不确定性越高

自信息：用于描述单个事件的不确定性

 优化交叉熵等价于优化相对熵

走进代码

构建虚拟数据

# fake data
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
#标签
target = torch.tensor([0, 1, 1], dtype=torch.long)

# ----------------------------------- CrossEntropy loss: reduction -----------------------------------
# flag = 0
flag = 1
if flag:
    # def loss function
    loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')
    loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')
    loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')

    # forward
    loss_none = loss_f_none(inputs, target)
    loss_sum = loss_f_sum(inputs, target)
    loss_mean = loss_f_mean(inputs, target)

    # view
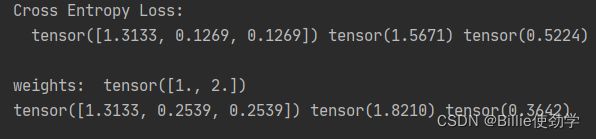
    print("Cross Entropy Loss:\n ", loss_none, loss_sum, loss_mean)

输出结果：

每个样本的loss、loss之和、loss取平均

 手动计算是否准确：

# --------------------------------- compute by hand
#flag = 0
flag = 1
if flag:

    idx = 0

    input_1 = inputs.detach().numpy()[idx]      # [1, 2]
    target_1 = target.numpy()[idx]              # [0]

    # 第一项
    x_class = input_1[target_1]

    # 第二项
    sigma_exp_x = np.sum(list(map(np.exp, input_1)))
    log_sigma_exp_x = np.log(sigma_exp_x)

    # 输出loss
    loss_1 = -x_class + log_sigma_exp_x

    print("第一个样本loss为: ", loss_1)

输出结果：

与前者一致

 对每个样本进行权值的缩放

# ----------------------------------- weight -----------------------------------
# flag = 0
flag = 1
if flag:
    # def loss function
    #有几个类，weight就要设几个值
    weights = torch.tensor([1, 2], dtype=torch.float)
    # weights = torch.tensor([0.7, 0.3], dtype=torch.float)

    loss_f_none_w = nn.CrossEntropyLoss(weight=weights, reduction='none')
    loss_f_sum = nn.CrossEntropyLoss(weight=weights, reduction='sum')
    loss_f_mean = nn.CrossEntropyLoss(weight=weights, reduction='mean')

    # forward
    loss_none_w = loss_f_none_w(inputs, target)
    loss_sum = loss_f_sum(inputs, target)
    loss_mean = loss_f_mean(inputs, target)

    # view
    print("\nweights: ", weights)
    print(loss_none_w, loss_sum, loss_mean)

输出结果：

与之前的结果进行对比，第一个标签为0，权重为1；后两个标签为1，权重为2 

可以观察到，第一个loss没有变；第二个和第三个loss变为原来的2倍

加权之后：sum直接求和，mean需要求加权平均

3.NLLLoss

nn.NLLLoss

功能：实现负对数似然函数中的负号功能

主要参数：

• weight：各类别的loss设置权值
• ignore_index：忽略某个类别
• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

 走进代码：

该公式只是对数据取负号操作

# ----------------------------------- 2 NLLLoss -----------------------------------
# flag = 0
flag = 1
if flag:

    weights = torch.tensor([1, 1], dtype=torch.float)

    loss_f_none_w = nn.NLLLoss(weight=weights, reduction='none')
    loss_f_sum = nn.NLLLoss(weight=weights, reduction='sum')
    loss_f_mean = nn.NLLLoss(weight=weights, reduction='mean')

    # forward
    loss_none_w = loss_f_none_w(inputs, target)
    loss_sum = loss_f_sum(inputs, target)
    loss_mean = loss_f_mean(inputs, target)

    # view
    print("\nweights: ", weights)
    print("NLL Loss", loss_none_w, loss_sum, loss_mean)

输出结果：

第一个值的标签是0，则对第一个数据的index=0的位置取负号

第二个和第三个值得标签是1，则对第二个和第三个数据的index=1的位置取负号

4.BCE

nn.BCELoss

功能：二分类交叉熵

注意事项：输入值取值在[0,1]，需要符合概率取值

主要参数：

• weight：各类别的loss设置权值
• ignore_index：忽略某个类别
• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

 yn是标签，yn = 0或者yn = 1

进入代码：

# ----------------------------------- 3 BCE Loss -----------------------------------
# flag = 0
flag = 1
if flag:
    inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
    target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

    target_bce = target


    # itarget 将输入值压缩到[0-1]
    inputs = torch.sigmoid(inputs)

    weights = torch.tensor([1, 1], dtype=torch.float)

    loss_f_none_w = nn.BCELoss(weight=weights, reduction='none')
    loss_f_sum = nn.BCELoss(weight=weights, reduction='sum')
    loss_f_mean = nn.BCELoss(weight=weights, reduction='mean')

    # forward
    loss_none_w = loss_f_none_w(inputs, target_bce)
    loss_sum = loss_f_sum(inputs, target_bce)
    loss_mean = loss_f_mean(inputs, target_bce)

    # view
    print("\nweights: ", weights)
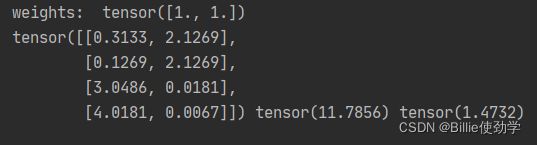
    print("BCE Loss", loss_none_w, loss_sum, loss_mean)

输出结果

每个神经元一一计算loss

5.BCEWithLogists Loss

nn.BCEWithLogists Loss

功能：结合Sigmoid与二分类交叉熵

注意事项：网络最后不加sigmoid函数

主要参数：

• pos_weight：正样本的权值
• weight：各类别的loss设置权值
• ignore_index：忽略某个类别
• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

 BCELoss中我们发现，如果输入数据不在[0,1]区间内就会报错，针对这一问题提出了nn.BCEWithLogists Loss

进入代码：

# ----------------------------------- 4 BCE with Logis Loss -----------------------------------
# flag = 0
flag = 1
if flag:
    inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
    target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

    target_bce = target

    # inputs = torch.sigmoid(inputs)

    weights = torch.tensor([1, 1], dtype=torch.float)

    loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none')
    loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum')
    loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean')

    # forward
    loss_none_w = loss_f_none_w(inputs, target_bce)
    loss_sum = loss_f_sum(inputs, target_bce)
    loss_mean = loss_f_mean(inputs, target_bce)

    # view
    print("\nweights: ", weights)
    print(loss_none_w, loss_sum, loss_mean)

输出结果：

pos_weight：

# --------------------------------- pos weight

# flag = 0
flag = 1
if flag:
    inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
    target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

    target_bce = target

    # itarget
    # inputs = torch.sigmoid(inputs)

    weights = torch.tensor([1], dtype=torch.float)
    pos_w = torch.tensor([3], dtype=torch.float)        # 3

    loss_f_none_w = nn.BCEWithLogitsLoss(weight=weights, reduction='none', pos_weight=pos_w)
    loss_f_sum = nn.BCEWithLogitsLoss(weight=weights, reduction='sum', pos_weight=pos_w)
    loss_f_mean = nn.BCEWithLogitsLoss(weight=weights, reduction='mean', pos_weight=pos_w)

    # forward
    loss_none_w = loss_f_none_w(inputs, target_bce)
    loss_sum = loss_f_sum(inputs, target_bce)
    loss_mean = loss_f_mean(inputs, target_bce)

    # view
    print("\npos_weights: ", pos_w)
    print(loss_none_w, loss_sum, loss_mean)

当pos_weight设置为1时，loss与前面一样

 若pos_weight设置为3

则对正样本所在的神经元乘3这个系数

target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

则对样本标签为1的位置进行3倍操作

6.nn.L1Loss

功能：计算input与target之差的绝对值

主要参数：

• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

代码：

set_seed(1)  # 设置随机种子

# ------------------------------------------------- 5 L1 loss ----------------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.ones((2, 2))
    target = torch.ones((2, 2)) * 3

    loss_f = nn.L1Loss(reduction='none')
    loss = loss_f(inputs, target)

    print("input:{}\ntarget:{}\nL1 loss:{}".format(inputs, target, loss))

7.nn.MSELoss

功能：计算input与target之差的平方

主要参数：

• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

 代码：

# ------------------------------------------------- 6 MSE loss ----------------------------------------------

    loss_f_mse = nn.MSELoss(reduction='none')
    loss_mse = loss_f_mse(inputs, target)

    print("MSE loss:{}".format(loss_mse))

8.SmoothL1Loss

功能：平滑的L1Loss

主要参数：

• reduction：计算模式，可为none/sum/mean
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

 

 代码：

# ------------------------------------------------- 7 Smooth L1 loss ----------------------------------------------
flag = 0
# flag = 1
if flag:
    inputs = torch.linspace(-3, 3, steps=500)
    target = torch.zeros_like(inputs)

    loss_f = nn.SmoothL1Loss(reduction='none')

    loss_smooth = loss_f(inputs, target)

    loss_l1 = np.abs(inputs.numpy())

    plt.plot(inputs.numpy(), loss_smooth.numpy(), label='Smooth L1 Loss')
    plt.plot(inputs.numpy(), loss_l1, label='L1 loss')
    plt.xlabel('x_i - y_i')
    plt.ylabel('loss value')
    plt.legend()
    plt.grid()
    plt.show()

9.PoissonNLLLoss

功能：泊松分布的负对数似然损失函数

主要参数：

• log_input：输入是否为对数形式，决定计算公式
• full：计算所有loss，默认为False
• eps：修正项，避免log(input)为nan

代码：

# ------------------------------------------------- 8 Poisson NLL Loss ----------------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.randn((2, 2))
    target = torch.randn((2, 2))

    loss_f = nn.PoissonNLLLoss(log_input=True, full=False, reduction='none')
    loss = loss_f(inputs, target)
    print("input:{}\ntarget:{}\nPoisson NLL loss:{}".format(inputs, target, loss))

10.KLDivergence Loss

功能：计算KLD（divergence），KL散度，相对熵

注意事项：需提前将输入计算log-probabilities，如通过nn.logsoftmax()

主要参数：

• reduction：计算模式，可为none/sum/mean/batchmean
  • batchmean：batchsize维度求平均值
  • none：逐个元素计算
  • sum：返回所有元素求和，返回标量
  • mean：加权平均，返回标量（默认）

代码：

# ------------------------------------------------- 9 KL Divergence Loss ----------------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
    # pytorch函数计算公式不是原始定义公式，其对输入默认已经取log了，在损失函数计算中比公式定义少了一个log（input）的操作
    # 因此公式定义里有一个log(y_i / x_i)，在pytorch变为了 log(y_i) - x_i，
    inputs = F.log_softmax(inputs, 1)
    target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)

    loss_f_none = nn.KLDivLoss(reduction='none')
    loss_f_mean = nn.KLDivLoss(reduction='mean')
    loss_f_bs_mean = nn.KLDivLoss(reduction='batchmean')

    loss_none = loss_f_none(inputs, target)
    loss_mean = loss_f_mean(inputs, target)
    loss_bs_mean = loss_f_bs_mean(inputs, target)

    print("loss_none:\n{}\nloss_mean:\n{}\nloss_bs_mean:\n{}".format(loss_none, loss_mean, loss_bs_mean))

11.Margin Ranking Loss

功能：计算两个向量之间的相似度，用于排序任务

特别说明：该方法计算两组数据之间的差异，返回一个n*n的loss矩阵

主要参数：

• margin：边界值，x1与x2之间的差异值
• reduction：计算模式，可为none/sum/mean

y = 1时，希望x1比x2大，当x1>x2时，不产生loss

y = -1时，希望x2比x1大，当x2>x1时，不产生loss

 

代码：

# ---------------------------------------------- 10 Margin Ranking Loss --------------------------------------------
flag = 0
# flag = 1
if flag:

    x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
    x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)

    target = torch.tensor([1, 1, -1], dtype=torch.float)

    loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')

    loss = loss_f_none(x1, x2, target)

    print(loss)

12.Multi Label Margin Loss

功能：多标签便捷损失函数

举例：四分类任务，样本x属于0类和3类，标签：[0,3,-1,-1],不是[1,0,0,1]

主要参数：

• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 11 Multi Label Margin Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    x = torch.tensor([[0.1, 0.2, 0.4, 0.8]])
    y = torch.tensor([[0, 3, -1, -1]], dtype=torch.long)

    loss_f = nn.MultiLabelMarginLoss(reduction='none')

    loss = loss_f(x, y)

    print(loss)

手动计算：

# --------------------------------- compute by hand
flag = 0
# flag = 1
if flag:

    x = x[0]
    item_1 = (1-(x[0] - x[1])) + (1 - (x[0] - x[2]))    # [0]
    item_2 = (1-(x[3] - x[1])) + (1 - (x[3] - x[2]))    # [3]

    loss_h = (item_1 + item_2) / x.shape[0]

    print(loss_h)

13.SoftMargin Loss

功能：计算二分类的logistic损失

主要参数：

• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 12 SoftMargin Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])
    target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)

    loss_f = nn.SoftMarginLoss(reduction='none')

    loss = loss_f(inputs, target)

    print("SoftMargin: ", loss)

14.MultiLabel SoftMargin Loss

功能：SoftMarginLoss多标签版本

主要参数：

• weight：各类别的loss设置权值
• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 13 MultiLabel SoftMargin Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.tensor([[0.3, 0.7, 0.8]])
    target = torch.tensor([[0, 1, 1]], dtype=torch.float)

    loss_f = nn.MultiLabelSoftMarginLoss(reduction='none')

    loss = loss_f(inputs, target)

    print("MultiLabel SoftMargin: ", loss)

15.Multi Margin Loss

功能：计算多分类的折页损失

主要参数：

• p：可选1或2
• weight：各类别的loss设置权值
• margin：边界值
• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 14 Multi Margin Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    x = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.5, 0.3]])
    y = torch.tensor([1, 2], dtype=torch.long)

    loss_f = nn.MultiMarginLoss(reduction='none')

    loss = loss_f(x, y)

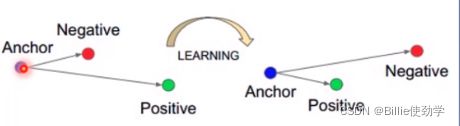
    print("Multi Margin Loss: ", loss)

16.Triplet Margin Loss

功能：计算三元组损失，人脸验证中常用

主要参数：

• p：范数的阶，默认为2
• margin：边界值
• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 15 Triplet Margin Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    anchor = torch.tensor([[1.]])
    pos = torch.tensor([[2.]])
    neg = torch.tensor([[0.5]])

    loss_f = nn.TripletMarginLoss(margin=1.0, p=1)

    loss = loss_f(anchor, pos, neg)

    print("Triplet Margin Loss", loss)

17.Hinge Embedding Loss

功能：计算两个输入的相似性，常用于非线性embedding和半监督学习

主要参数：

• margin：边界值
• reduction：计算模式，可为none/sum/mean

代码： 

# ---------------------------------------------- 16 Hinge Embedding Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    inputs = torch.tensor([[1., 0.8, 0.5]])
    target = torch.tensor([[1, 1, -1]])

    loss_f = nn.HingeEmbeddingLoss(margin=1, reduction='none')

    loss = loss_f(inputs, target)

    print("Hinge Embedding Loss", loss)

18.Cosine Embedding Loss

功能：采用余弦相似度计算两个输入的相似性

主要参数：

• margin：可取值[-1,1]，推荐为[0,0.5]
• reduction：计算模式，可为none/sum/meam

代码：

# ---------------------------------------------- 17 Cosine Embedding Loss -----------------------------------------
flag = 0
# flag = 1
if flag:

    x1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
    x2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])

    target = torch.tensor([[1, -1]], dtype=torch.float)

    loss_f = nn.CosineEmbeddingLoss(margin=0., reduction='none')

    loss = loss_f(x1, x2, target)

    print("Cosine Embedding Loss", loss)

19.CTC Loss

功能：计算CTC损失，解决时序类数据的分类

Connectionist Temporal Classification

主要参数：

• blank：blank label
• zero_infinity：无穷大的值或梯度置0
• reduction：计算模式，可为none/sum/mean

代码：

# ---------------------------------------------- 18 CTC Loss -----------------------------------------
# flag = 0
flag = 1
if flag:
    T = 50      # Input sequence length
    C = 20      # Number of classes (including blank)
    N = 16      # Batch size
    S = 30      # Target sequence length of longest target in batch
    S_min = 10  # Minimum target length, for demonstration purposes

    # Initialize random batch of input vectors, for *size = (T,N,C)
    inputs = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()

    # Initialize random batch of targets (0 = blank, 1:C = classes)
    target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)

    input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
    target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)

    ctc_loss = nn.CTCLoss()
    loss = ctc_loss(inputs, target, input_lengths, target_lengths)

    print("CTC loss: ", loss)

四、优化器（一）

1.什么是优化器

pytorch的优化器：管理并更新模型中可学习参数的值，使得模型输出更接近真实标签

导数：函数在指定坐标轴上的变化率

方向导数：指定方向上的变化率

梯度：一个向量，方向为方向导数取得最大值的方向

梯度下降：朝着梯度下降的负方向去变化，下降是最快的

2.optimizer的属性和方法

（1）Optimizer的基本属性

• defaults：优化器的超参数（存储lr，weight_decay等）
• state：参数的缓存，如momentum的缓存
• param_groups：管理的参数组
• _step_count：记录更新次数，学习率调整中使用

（2）基本方法

• zero_grad()：清空所管理参数的梯度

pytorch特性：张量梯度不自动清零,每一次反向传播采用auto_grad去计算梯度时，会把每次计算的梯度值加到张量grad属性中。例如：grad中存储了一个梯度值为-3，下一个要存入的值为3，则两个梯度值相加变为0。梯度置在grad中是累加的，每次都需要手动清零。

•  step：执行一步更新（更新权重） 

• add_param_group()：添加参数组，不同的组有不同的超参数

例如：fine_tune中，我们对模型前面这些特征提取部分的权重参数，希望学习率小一些，更新的慢一些，将其设置为一组参数；而在后面的全连接层，我们希望其学习率大一些，更新的快一些，这些设置为一组参数。

•  state_dict()：获取优化器当前状态信息字典
• load_state_dict()：将状态信息字典加载到优化器中

这两个方法的作用是回复断点的训练，例如，一个模型需要训练十天，而在第三天的时候因为断电等问题停止了训练，而我们重新启动训练时就不需要从0开始了，直接从断点处加载状态信息，继续训练。

 走入代码：

step 1：构建优化器

在优化器的定义这里设定断点，进行debug

optimizer = optim.SGD(net.parameters(), lr=LR, momentum=0.9)   

跳入到函数SGD的init函数，进行一系列参数合法性判断

 再执行到最后一行，进入它的父类，Optimizer类

这里面存放着前面介绍的优化器的参数

 我们看看defaults参数里面有什么

里面存放着五个参数

运行完init跳出函数

优化器执行完毕，我们看一下它的属性信息

optimizer中有三个属性 

 我们再看一看param_groups中有什么

param_groups中的params中存放着模型中的每一个可学习参数

step 2：优化器是怎么样运行的

 首先将梯度清零

optimizer.zero_grad()

使用step更新权值 

 optimizer.step()

下面来学习一下这五个参数具体的使用

（1）构建可学习参数和学习率

set_seed(1)  # 设置随机种子

#构建可学习参数
weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))

#传入可学习参数，学习率设置为1
optimizer = optim.SGD([weight], lr=0.1)

（2）step：进行一步更新

# ----------------------------------- step -----------------------------------
# flag = 0
flag = 1
if flag:
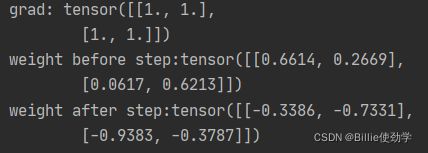
    print("weight before step:{}".format(weight.data))
    optimizer.step()        # 修改lr=1 0.1观察结果
    print("weight after step:{}".format(weight.data))

输出结果：

梯度下降：让权值参数朝着梯度的负方向更新，即参数值加负的梯度

梯度为1，lr = 1，每个元素都会在原来的基础上减1

 若lr = 0.1，则每个元素都在原来的基础上减0.1（1*0.1）

 （3）zero_grad：更新梯度

# ----------------------------------- zero_grad -----------------------------------
# flag = 0
flag = 1
if flag:

    print("weight before step:{}".format(weight.data))
    optimizer.step()        # 修改lr=1 0.1观察结果
    print("weight after step:{}".format(weight.data))

    print("weight in optimizer:{}\nweight in weight:{}\n".format(id(optimizer.param_groups[0]['params'][0]), id(weight)))

    print("weight.grad is {}\n".format(weight.grad))
    optimizer.zero_grad()
    print("after optimizer.zero_grad(), weight.grad is\n{}".format(weight.grad))

 进行清零操作后，梯度变为0

 此外，我们发现，优化器中管理的weight的内存地址，和其真实的内存地址是一致的

所以优化器中保存的是参数地址，而不是参数本身，节省了内存的消耗

 （4）add_param_groups：增加组参数

# ----------------------------------- add_param_group -----------------------------------
flag = 0
# flag = 1
if flag:
    print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

    w2 = torch.randn((3, 3), requires_grad=True)

    optimizer.add_param_group({"params": w2, 'lr': 0.0001})

    print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

输出结果：

设置两组参数，以针对不同问题设置不同参数

（5）state_dict：保存优化器的状态信息

进行十次更新

# ----------------------------------- state_dict -----------------------------------
flag = 0
# flag = 1
if flag:

    optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
    opt_state_dict = optimizer.state_dict()

    print("state_dict before step:\n", opt_state_dict)

    for i in range(10):
        optimizer.step()

    print("state_dict after step:\n", optimizer.state_dict())
    #保存状态信息
    torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

输出结果：

更新权重前，state中没有任何信息

更新权重后，state中保存了状态信息

将状态信息保存为pkl文件，在相应目录下就可以看到这个文件

（6）load_state_dict：加载状态信息

在之前的十次更新后继续更新，而非从头更新

读取存有状态信息的文件

# -----------------------------------load state_dict -----------------------------------
flag = 0
# flag = 1
if flag:

    optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
    state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

    print("state_dict before load state:\n", optimizer.state_dict())
    optimizer.load_state_dict(state_dict)
    print("state_dict after load state:\n", optimizer.state_dict())

输出结果：

加载之前state中没有信息

加载之后，调用了之前的状态信息文件

五、优化器（二）

1.learning rate 学习率

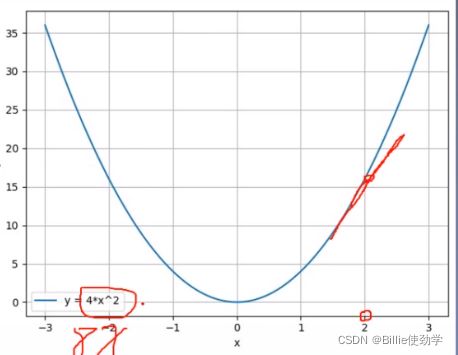
梯度下降：

g(wi)为梯度值，等于y的导数

 

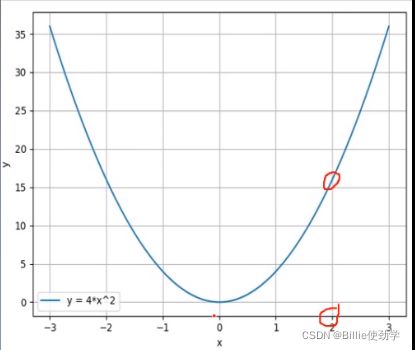
我们用梯度的下降的方法期望函数值越来越小，但是如上图所示，函数值y越来越大。

这是什么原因呢？

代码：

#构建一个函数
def func(x_t):
    """
    y = (2x)^2 = 4*x^2      dy/dx = 8x
    """
    return torch.pow(2*x_t, 2)


# init
x = torch.tensor([2.], requires_grad=True)

# ------------------------------ gradient descent ------------------------------
# flag = 0
flag = 1
if flag:
    #记录loss和迭代次数用来画loss曲线
    iter_rec, loss_rec, x_rec = list(), list(), list()

    lr = 0.5   # /1. /.5 /.2 /.1 /.125
    max_iteration = 4  # /1. 4     /.5 4   /.2 20 200

    for i in range(max_iteration):

        y = func(x)
        y.backward()

        print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
            i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()))

        x_rec.append(x.item())

        x.data.sub_(lr * x.grad)    # x -= x.grad  数学表达式意义:  x = x - x.grad    # 0.5 0.2 0.1 0.125
        x.grad.zero_()

        iter_rec.append(i)
        loss_rec.append(y.detach().numpy())

    plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
    plt.xlabel("Iteration")
    plt.ylabel("Loss value")

    x_t = torch.linspace(-3, 3, 100)
    y = func(x_t)
    plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
    plt.grid()
    y_rec = [func(torch.tensor(i)).item() for i in x_rec]
    plt.subplot(122).plot(x_rec, y_rec, '-ro')
    plt.legend()
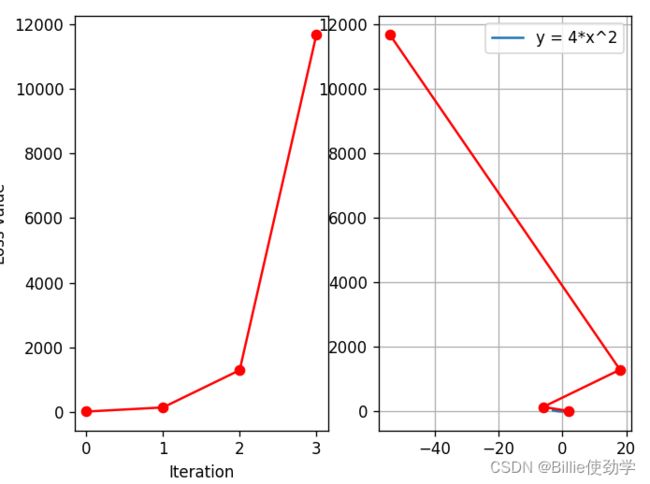
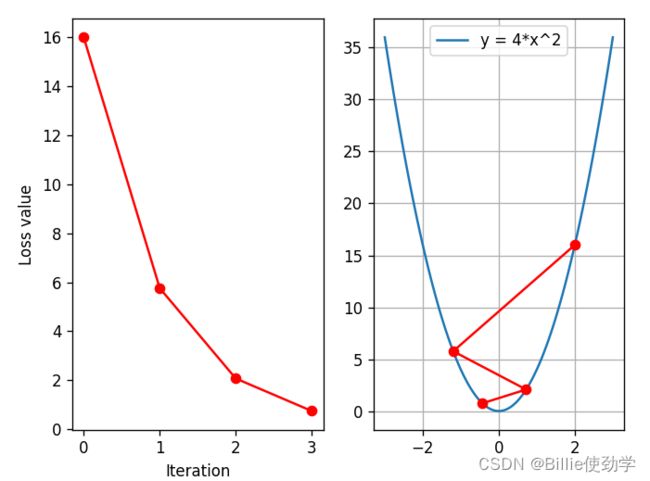
    plt.show()

输出结果：

这里迭代了四次，可以看到，梯度发生了爆炸，loss值也越来越大，为什么y越来越大呢？

 

 梯度下降：

因为g(wi)太大而导致wi+1也越来越大，一般会在它前面乘个系数来缩小尺度

学习率（learning rate）控制更新的步伐，以免发生loss值得激增和梯度的爆炸

下面我们通过代码看一下什么样的学习率可以使loss是下降的

当我们将学习率设为0.2后，l可以看到loss是下降的

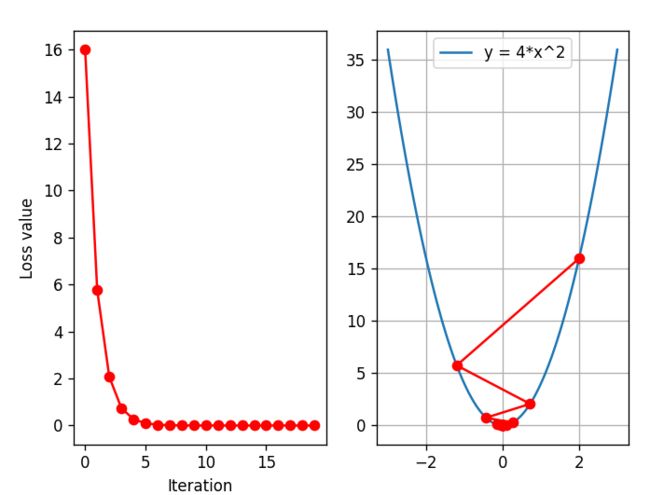
我们把迭代次数设置的大一点，看loss是否还会继续降低

可以看到，loss一致在降低

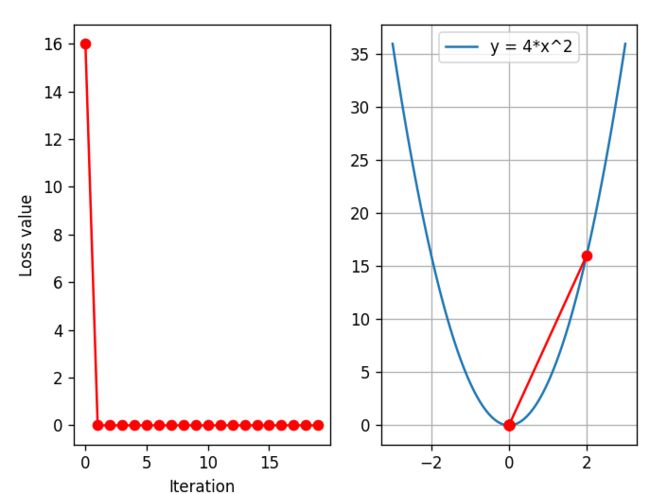
 当lr设置为0.125，loss值就可以一步到达0

 

我们设置多个学习率来观察不同大小的lr对loss 的影像

代码：

# ------------------------------ multi learning rate ------------------------------

# flag = 0
flag = 1
if flag:
    iteration = 100
    num_lr = 10
    lr_min, lr_max = 0.01, 0.2  # .5 .3 .2

    lr_list = np.linspace(lr_min, lr_max, num=num_lr).tolist()
    loss_rec = [[] for l in range(len(lr_list))]
    iter_rec = list()

    for i, lr in enumerate(lr_list):
        x = torch.tensor([2.], requires_grad=True)
        for iter in range(iteration):

            y = func(x)
            y.backward()
            x.data.sub_(lr * x.grad)  # x.data -= x.grad
            x.grad.zero_()

            loss_rec[i].append(y.item())

    for i, loss_r in enumerate(loss_rec):
        plt.plot(range(len(loss_r)), loss_r, label="LR: {}".format(lr_list[i]))
    plt.legend()
    plt.xlabel('Iterations')
    plt.ylabel('Loss value')
    plt.show()

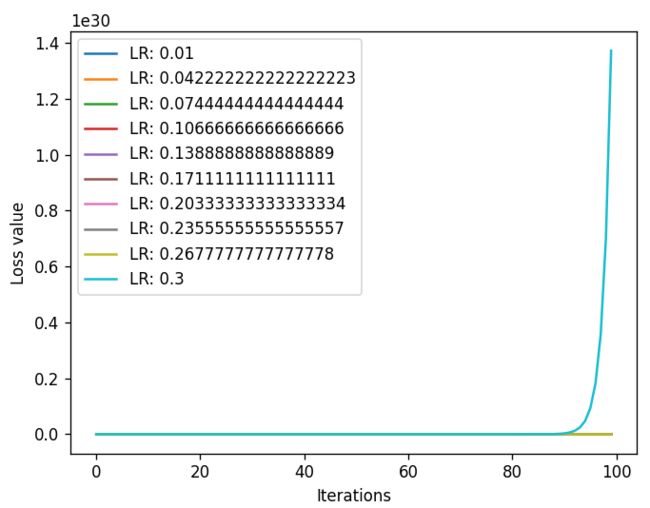
输出结果：

当lr的最大值设置为0.3时，可以看到，loss还是激增的

 所以将lr的最高设置到0.2

上图可以看到，lr不是越大，loss下降越快，而是当lr = 0.136时，loss下降最快，所以当lr的设置越靠近0.125，loss下降越快。

综上所述，lr 从来控制更新的步伐，设置学习率时，不能设置的太大，如0.3，0.5，此时的loss值是激增，容易引发梯度爆炸；也不能设置太小，设置太小就很难收敛

2.momentum 动量

momentum（动量、冲量）：结合当前梯度与上一次更新信息，用于当前更新

 每次更新朝着梯度下降最快的方向进行，且步长是固定的

叠加上一次的更新信息，使步长变大，可以更快的到达最低点

指数加权平均：在时间序列中经常使用的求取平均值的方法，求取当前时刻的平均值，距离平均值越近的参数值，参考性越大，所占的权重也越大

代码：

#构建权重的计算公式，观察每一个时刻的权重
def exp_w_func(beta, time_list):
    return [(1 - beta) * np.power(beta, exp) for exp in time_list]


beta = 0.9
num_point = 100
time_list = np.arange(num_point).tolist()

# ------------------------------ exponential weight ------------------------------
# flag = 0
flag = 1
if flag:
    weights = exp_w_func(beta, time_list)

    plt.plot(time_list, weights, '-ro', label="Beta: {}\ny = B^t * (1-B)".format(beta))
    plt.xlabel("time")
    plt.ylabel("weight")
    plt.legend()
    plt.title("exponentially weighted average")
    plt.show()

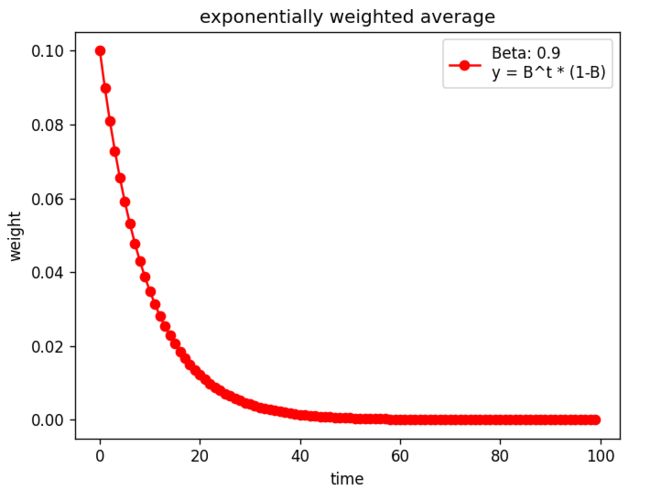
    print(np.sum(weights))

输出结果：

当time = 0，时权重为0.1，越往前权重越小，距离当前时刻越远，对当前时刻平均值的影响就越小

设置不同的贝塔，看一下权重的变化

# ------------------------------ multi weights ------------------------------
flag = 0
# flag = 1
if flag:
    beta_list = [0.98, 0.95, 0.9, 0.8]
    w_list = [exp_w_func(beta, time_list) for beta in beta_list]
    for i, w in enumerate(w_list):
        plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
        plt.xlabel("time")
        plt.ylabel("weight")
    plt.legend()
    plt.show()

输出结果：

贝塔可以理解为记忆周期的概念，贝塔值越小，记忆周期越短

如贝塔 = 0.8时，记忆周期就很多，仅在20左右

贝塔 = 0.98时，记忆周期就比较长

通常，我们会将贝塔设置为0.9，它可以更关注当前时刻十天左右的情况。10 =  1/(1-)）

 梯度下降（原来的梯度下降方式）：

 pytorch中更新公式（加入动量之后的梯度下降方式）：

这里lr乘的不是梯度了，而是变化量，当前的变化量也会考虑到之前的梯度

 

代码：带动量的loss变化情况

# ------------------------------ SGD momentum ------------------------------
# flag = 0
flag = 1
if flag:
    def func(x):
        return torch.pow(2*x, 2)    # y = (2x)^2 = 4*x^2        dy/dx = 8x

    iteration = 100
    m = 0.9     # .9 .63

    lr_list = [0.01, 0.03]

    momentum_list = list()
    loss_rec = [[] for l in range(len(lr_list))]
    iter_rec = list()

    for i, lr in enumerate(lr_list):
        x = torch.tensor([2.], requires_grad=True)

        momentum = 0. if lr == 0.03 else m
        momentum_list.append(momentum)

        optimizer = optim.SGD([x], lr=lr, momentum=momentum)

        for iter in range(iteration):

            y = func(x)
            y.backward()

            optimizer.step()
            optimizer.zero_grad()

            loss_rec[i].append(y.item())

    for i, loss_r in enumerate(loss_rec):
        plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))
    plt.legend()
    plt.xlabel('Iterations')
    plt.ylabel('Loss value')
    plt.show()

输出结果：

lr设置为0.01和0.03，两个都不加动量的输出结果

可以看到，学习率大的收敛更快

那我们为学习率小的加上动量，它的收敛速度会比大学习率快吗？ 

将动量设为0.9时

在最开始的低点，是比lr = 0.03更快的，但是又开始震荡， 这说明动量设置的太大了

 动量设小一点

此时，可以看到，小学习率下降的更快了

所以合适的动量可以加速loss的下降

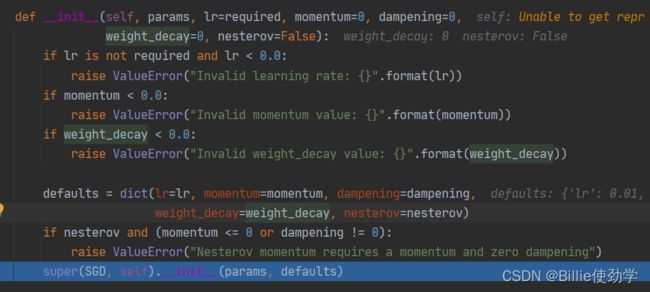
3.torch.optim.SGD

主要参数：

• params：管理的参数组list，list的元素是字典，key = params主要用来管理模型实际参数
• lr：初始学习率
• momentum：动量系数，贝塔
• weight_decay：L2正则化系数
• nesterov：是否采用NAG梯度下降方法，布尔变量

4.Pytorch的十种优化器

六、学习率调整策略

1.为什么要调整学习率？

梯度下降：

学习率（learning rate）控制更新的步伐

一般前期学习率会设置的比较大，后期设置的比较小

以打高尔夫为例，开始的时候击球的力度会大一些，让高尔夫球落在洞口附近

然后来到洞口，这次就需要小一点的击球力度，让球逐渐靠近洞口

 

 设置较大的学习率，让loss快速下降，此时曲线是震荡的

如果继续采用较大的学习率，那loss就无法继续下降

class_LRScheduler

主要属性：

• optimizer：关联的优化器
• last_epoch：记录epoch数
• base_lrs：记录初始学习率 

主要方法：

• step()：更新下一个epoch的学习率
• get_lr()：虚函数，计算下一个epoch的学习率

进入代码：

调试这一行代码

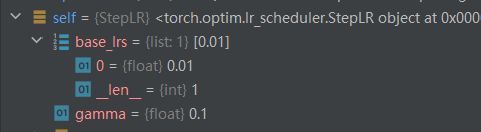
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1)     # 设置学习率下降策略

进入了LR类

 进入父类_LRscheduler 

32行关联优化器

43行存放多个学习率

44行记录epoch数目，学习率更新时用到

更新下一个epoch的学习率

scheduler.step()  # 更新学习率

进入函数

epoch加一

 修改参数组的学习率

 进入value

下一个epoch的lr计算

2.pytorch的六种学习率调整策略

（1）StepLR

功能：等间隔调整学习率

主要参数：

• step_size：调整间隔数（每个n个epoch调整学习率）
• gamma：调整系数

调整方式：lr = lr * gamma

代码：

构建数据和学习率

torch.manual_seed(1)

LR = 0.1
iteration = 10
max_epoch = 200
# ------------------------------ fake data and optimizer  ------------------------------

weights = torch.randn((1), requires_grad=True)
target = torch.zeros((1))

optimizer = optim.SGD([weights], lr=LR, momentum=0.9)

# ------------------------------ 1 Step LR ------------------------------
flag = 0
# flag = 1
if flag:

    scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1)  # 设置学习率下降策略

    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):

        # 获取当前lr，新版本用 get_last_lr()函数，旧版本用get_lr()函数，具体看UserWarning
        lr_list.append(scheduler_lr.get_last_lr())
        epoch_list.append(epoch)

        for i in range(iteration):

            loss = torch.pow((weights - target), 2)
            loss.backward()

            optimizer.step()
            optimizer.zero_grad()

        scheduler_lr.step()

    plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

输出结果：

（2）MultiStepLR

功能：按给定间隔调整学习率

主要参数：

• milestones：设定调整时刻数 eg:自定义间隔数[50,125,180]
• gamma：调整系数

调整方式：lr = lr * gamma

代码：

# ------------------------------ 2 Multi Step LR ------------------------------
# flag = 0
flag = 1
if flag:

    milestones = [50, 125, 160]
    scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.1)

    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):

        lr_list.append(scheduler_lr.get_lr())
        epoch_list.append(epoch)

        for i in range(iteration):

            loss = torch.pow((weights - target), 2)
            loss.backward()

            optimizer.step()
            optimizer.zero_grad()

        scheduler_lr.step()

    plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

输出结果：

（3）ExponentialLR

功能：按指数衰减调整学习率

主要参数：

• gamma：指数的底（一般设置为接近1的一个数）

调整方式：lr = lr * gamma ** epoch

代码：

# ------------------------------ 3 Exponential LR ------------------------------
# flag = 0
flag = 1
if flag:

    gamma = 0.95
    scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

输出结果：

（4）CosineAnnealingLR

功能：余弦周期调整学习率

主要参数：

• T_max：下降周期，半个周期（整个周期为两倍的T_max）
• eta_min：学习率下限（通常设置为0）

调整方式：

代码：

# ------------------------------ 4 Cosine Annealing LR ------------------------------
# flag = 0
flag = 1
if flag:

    t_max = 50
    scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=t_max, eta_min=0.)

输出结果：

（5）ReduceLRonPlateau

功能：监控指标，当指标不再变化则调整

主要参数：

• mode：min/max 两种模式
  • min：如果监控指标不再下降则调整学习率，一般用来监控loss
  • max：如果监控指标不再上升则调整学习率，一般用来监控accuracy
• factor：调整系数
• patience：“耐心”，接受几次不变化
  • 监控指标连续n次没有下降/增长，则调整学习率
• cooldown：“冷却时间”，停止监控一段时间
  • 调整完学习率后一段时间内不再监控指标
• verbose：是否打印日志
• min_lr：学习率下限
• eps：学习率衰减最小值

代码：

# ------------------------------ 5 Reduce LR On Plateau ------------------------------
# flag = 0
flag = 1
if flag:
    loss_value = 0.5
    accuray = 0.9

    factor = 0.1
    mode = "min"
    patience = 10
    cooldown = 10
    min_lr = 1e-4
    verbose = True

    scheduler_lr = optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, mode=mode, patience=patience,
                                                        cooldown=cooldown, min_lr=min_lr, verbose=verbose)

    for epoch in range(max_epoch):
        for i in range(iteration):

            # train(...)

            optimizer.step()
            optimizer.zero_grad()

        #if epoch == 5:
        #    loss_value = 0.4
        #放入监控标量
        scheduler_lr.step(loss_value)

输出结果：

min模式：冷却10个epoch，监控10个epoch

当第五个epoch的loss下降了

（6）LambdaLR

功能：自定义调整策略

主要参数：

• lr_lambda：function or list

代码：

# ------------------------------ 6 lambda ------------------------------
# flag = 0
flag = 1
if flag:

    lr_init = 0.1

    weights_1 = torch.randn((6, 3, 5, 5))
    weights_2 = torch.ones((5, 5))

    optimizer = optim.SGD([
        {'params': [weights_1]},
        {'params': [weights_2]}], lr=lr_init)

    lambda1 = lambda epoch: 0.1 ** (epoch // 20)
    lambda2 = lambda epoch: 0.95 ** epoch

    scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])

    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):
        for i in range(iteration):

            # train(...)

            optimizer.step()
            optimizer.zero_grad()

        scheduler.step()

        lr_list.append(scheduler.get_lr())
        epoch_list.append(epoch)

        print('epoch:{:5d}, lr:{}'.format(epoch, scheduler.get_lr()))

    plt.plot(epoch_list, [i[0] for i in lr_list], label="lambda 1")
    plt.plot(epoch_list, [i[1] for i in lr_list], label="lambda 2")
    plt.xlabel("Epoch")
    plt.ylabel("Learning Rate")
    plt.title("LambdaLR")
    plt.legend()
    plt.show()

输出结果：

lambda1：每个20个epoch进行调整

3.学习率调整小结

（1）有序调整

Step、MultiStep、Exponential和CosineAnnealing

（2）自适应调整

ReduceLROnPlateau

（3）自定义调整

Lambda

PS：学习率初始化一般设置为0.01，0.001，0.0001等

如何搜索最大学习率，参考：