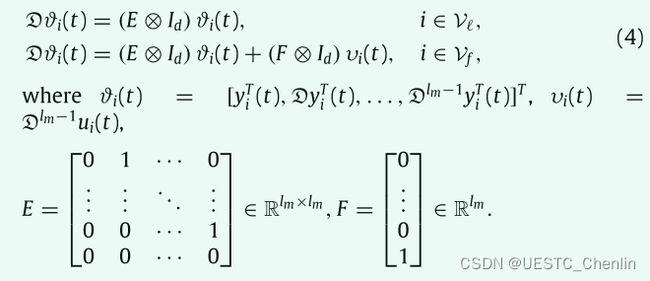【论文笔记】Affine formation maneuver control of high-order multi-agent systems over directed networks
【作者】:赵世钰
【刊物】：Automatica
相比与2018年的那篇文章，这一篇支持针对更高阶的系统，而且是有向图。
摘要：为了驱动一组智能体以期望的集合形式连续机动，本文研究了任意维有向网络化高阶多智能体系统的分布式编队机动控制问题。与传统方法中目标队形是时不变的不同，我们提出了一种基于仿射变换性质的仿射队形方法，其中目标队形可以是时变的，并且可以从给定的标称队形进行仿射变换。本文给出并证明了实现有向图仿射可定性的一个充要条件，它只需要leaders有一个几何的队形，并且followers对leaders子集是可访问的。为了实现整个编队的机动，假设领导者决定整个编队的机动动作，然后提出了任意阶积分系统的followers控制算法来跟踪时变目标编队，并证明了跟踪误差的全局收敛性。此外，本文还研究了存在非均匀时延时编队机动的实际问题。最后，通过二维和三维仿真算例验证了理论结果的有效性。
1.引言
本文研究了一种多智能体编队机动控制任务，以分布式引导智能体作为一个整体进行机动，从而可以实现任意维度的平移、方向、尺度变换和其他运动，以及具有任何给定初始队形的期望几何图案。所需的模式和机动对于一些复杂的任务至关重要，例如避开障碍物和通过狭窄的走廊。
虽然现有文献中有许多分布式编队控制方法，但大多数方法都不能解决本文研究的编队机动控制任务。这些方法可以根据目标编队所需几何图案的定义进行分类。 在最近的流行的三种研究方法中（Oh，Park和Ahn，2015；Zhu，Xie，Han，Meng和Teo，2017），例如，目标队形是根据相邻agent的相对位移（Dong和Hu，2017）、相对距离（Sun，Park，Anderson和Ahn，2017）或相对方位（Zhao和Zelazo，2019）来定义的。目标形状随时间变化的情况尚未得到充分解决。受这三种方案缺点的启发，科学家和工程师试图将特殊共识的特性集成到编队机动控制器的设计过程中。然后，许多新类型的常数约束被用于定义目标队形，如复杂拉普拉斯体（林、王、韩和傅，2014）和应力矩阵（赵，2018）。基于复杂拉普拉斯算子的控制方法可以同时执行平移、旋转和缩放编队机动（Han、Wang、Lin和Zheng，2016），但它仅限于平面内。后一种方法对任意维所需目标编队的任何仿射变换都是不变的。通过结合仿射变换和应力矩阵的特性，赵（2018）提出了一种仿射编队机动控制器，以实现各种机动，例如目标编队的平移、旋转、缩放，甚至形状变形。
编队机动的有向网络和高阶动力学模型是现实世界实现的两个具有挑战性的问题，它们还没有得到很好的解决。Zhao (2018) 中基于应力矩阵的编队机动控制协议只能应用于简单的条件，即无向图和低阶积分器动力学模型。此外，相邻agent之间的网络通常具有方向性，Zhao (2018) 中的双向测量很难实现。对于有向图形案例，Xu、Zhao、Luo 和 You (2018) 提出了基于有符号拉普拉斯算子的编队机动控制方案。有符号的拉普拉斯算子为获得各种编队机动行为提供了强大的求解器。在研究了处理多智能体系统的现有文献后（Li, Ren, Liu, & Fu, 2013; Meng, Lin, & Ren, 2012; Ren, 2007, 2008; Song, Cao, & Yu, 2010），其中的高阶积分动力学模型具有被归类为一般线性动力学的特殊情况的方法，这在 Cheng, Wang, Hou 和 Tan (2016) 和 Cheng, Wang, Ren 和侯（2016）中描述的轨迹跟踪问题中起着至关重要的作用。在实践中，每个leader的运动可以简化为相应维度的一系列合适的参考点，通过这些点的适当阶轨迹是通过样条或多项式插值生成的（Richter, Bry, & Roy, 2016;徐、赖、李、罗和尤，2019）。然后，followers被控制去跟踪这些生成的leaders轨迹。因此，无论leaders和followers是同构的还是异构的，都可以处理编队机动控制问题。需要指出的是，leaders通常只占整个编队的一小部分，而为了编队的机动性，他们的轨迹可以由智能路径规划器生成。
我们还处理了现有工作中另外两个未触及的编队机动实际问题。首先，多智能体编队控制器的性能通常会受到信息流内部各种时延的影响。现有的延时算法可分为均匀型和非均匀型（董、韩、李、陈、任，2016；董、李、任、中，2015；侯，傅，张，吴，2017；黄，方，窦，陈，2014）。出于应用的动机，由测量约束引起的时间延迟最好用非均匀的时间延迟来建模。其次，对于比例 (P) 型或比例导数 (PD) 型协议，在某些情况下，例如出现leaders的恒定输入时，leaders所引起的稳态编队误差是无法消除的。为了解决这一限制，增加了编队误差的积分项，控制器变为比例积分 (PI) 型或比例积分微分 (PID) 型。基于Lombana和Di Bernardo (2015,2016) 中PID型算法的特性，如果leaders和followers是异构的，并且leaders的轨迹具有更高的阶数，那么编队误差的高阶积分和导数项可以集成到控制器中。
主要贡献包括三个方面：
1）分析证明了有向图仿射定位性的充分必要条件，该条件在任意维度上都成立。 优于我们之前的工作（Xu et al., 2018; Zhao, 2018），提供了一个更灵活的条件，即仅leader子系统的几何的部分标称队形。
2）leaders的运动可以决定整个编队机动动作，这些动作表示为连接的多项式轨迹。 然后，我们提出了一种n阶 PI型线性编队机动控制律用于高阶积分器模型的followers。 还提供了跟踪误差的全局收敛性分析。
3）我们在存在实际限制的情况下处理仿射编队机动，例如，信息交换时存在时间延迟，与时域Lyapunov函数方法不同（Dong等人，2016年，2015年），延迟的上界在频域得到证明，并且延迟可以是非均匀的和时变的。
2.预备条件和问题陈述
2.1 有向图理论
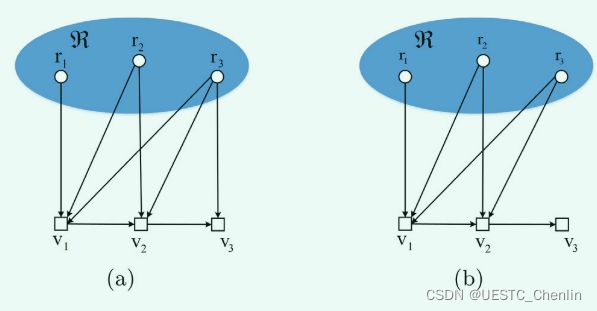
一条路径是由有向图的边组成的序列，在这篇文章中假设有向图没有环。对于有向图
而言，我们引用了k-可达(k-reachable)，k-rooted，spanning k-tree的概念.3-可达和非3-可达对应的概念阐述在图1中。（这些概念来源于lin 2016 TAC论文：Necessary and Sufficient Graphical Conditions for Affine Formation Control）
图1：用两个例子来说明3可达的条件和非3可达的条件。(a)所有节点v1、v2和v3都是根集R={r1、r2、r3}的3-可达节点，并且存在一个spanning-3树。(b)删除节点v2后，节点v3不是根集R的3-可达的节点。
后续，我们介绍了一种特殊的拉普拉斯算子，有符号拉普拉斯
,与图的真实权重相关。对于复拉普拉斯而言，非对角元素
当j是i的邻居，否则非对角元素为0，对角元素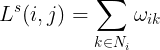
，此外通常是不对称矩阵，
2.2 问题陈述
agents通过有向交互图G交换信息，并假设每个领导者不与其他领导者交互，而是从follower那里传递信息。编队(G,y)表示有向图G，其位置yi从第i个节点映射。G的标准队形为
。标准队形r的仿射图为
,
是仿射变换。
假定leadr-i沿轨迹的n阶多项式轨迹运动
在本文中，我们要解决以下问题：
问题1。通过有向交互图，可以实现高阶多Agent系统的编队机动，使得所有Agent总是在目标编队内。
问题2。在非均匀时滞图形条件下，也需要设计相应的仿射编队机动控制器。
3.主要结果
3.1 仿射可定位的属性
可定位性揭示了网络是否可以通过leaders位置和邻居间的相对信息进行定位。基于网络可定位性和仿射变换，如果同时满足以下两个条件，则称标准队形(G，r)仿射可定位：
1） 当leaders满足![\large [p^T_l,p^T_f]^T\in A(r)](http://img.e-com-net.com/image/info8/6f19acbd0d6146d6822599ea3f7b5f4a.gif)
，
可以被
确定。（意思就是编队所有成员的位置都处于仿射图像中）。
2）对图G和位置y而言，图G的复拉普拉斯算子满足
在这个定义中，第一个条件是选择领导者，第二个条件是考虑有向图条件。在此节中，我们作出如下假设，并推导出满足仿射可定位的充要条件定理。
假设1.
在给定标准队形
中的leaders队形
满足
affine span in 
定理1.在假设1的条件下，给定的N个agent的标准队形是仿射可定位的，当且仅当有d+1个leaders,并且每个followers是(d+1)可达的。
证明：
充分性：有向图G的基础图必定是(d+1)-rooted的，而且有(d+1)生成树。有d+1个leaders和N-d-1个followers,图G的复拉普拉斯算子，必定包含(d+1)的全0行，那么可被划分为以下4块。
（是N行N列的矩阵。）
这意味着
以及
是非奇异的。
必要性：
现在，提供关于标称队形的有向图条件的另一个假设。
假设2.假设有向图G的根集有d+1个leaders,那么从leaders出发，每个followers是d+1-可达的。
假设1和假设2揭示了一个重要的数学前提：符号拉普拉斯的一个分块必须是非奇异的。此外，agents的数量
因为至少要有一个follower。给定满足假设1和2的标准队形,它具有性质
.在本文中，我们假设leader的队形总是在期望的目标队形之内，在所有时间，
,然后编队机动的控制目标变为去设计followers的控制律
去实现
。
3.2 仿射编队机动控制律
对于一个实际的任务，我们不能精确地获得领导者的精确动力学模型，而只能将leaders的轨迹测量值 (式1) 作为参考信号。第i个follower的m阶动力学可以描述为:
提出n阶PI型控制律(即控制律3)。m:阶数，n:轨迹多项式的阶数。 n=2m-1
由于假设1和2，满足非奇异性，存在排列矩阵M
定理2.在假设1和2的条件下，如果leaders按多项式轨迹
运动,在控制律(3)下的跟踪误差全局收敛，当且仅当
是Hurwitz的，跟踪误差以指数速度收敛到0，其中xx是Jordan标准型的对角线元素。
证明：
当定理2被证明之后，控制增益矩阵K的设计方法需要通过如下定理提供。
定理3.如果是Hurwitz的，那么![\large K=c[Re(\lambda_1)]^{-1}R^{-1}F^TP](http://img.e-com-net.com/image/info8/792c28d9fc2f480dab823b1c0d4746d4.gif){kind=small}
，阈值常量c>0.5,P是代数Riccati方程的正解
证明：
备注1. 本文采用leader-follower 结构，仿射编队控制类似于Cheng，Wang，Ren 等人的containment control(2016)。因为有向图形结构中有多个领导者。然而，follwers的containment control不能用于形成特定的形状，它们的位置随机定位在leaders的凸包内。仿射编队控制方法可以应用于所需的目标编队形状，无论follwers是否在leaders生成的凸包内，follwers者都可以收敛到指定的目标编队。此外，与 Cheng、Wang、Ren 等人(2016)的控制律相比。我们需要预乘一个附加参数 di 以构造一个稳定的对角矩阵 D。然后，D 可以将的负实部特征值放入右半平面。
备注2.在应用PI策略的实际实践中，较小的测量误差可能会放大follwers的跟踪误差。这可能导致积分项不能收敛，积分动作可视为次级频率控制（Emma&Sandberg，2017）。积分动作的作用是消除由P或PD控制引起的任何固定频率控制误差，并且瞬态性能也同时改善。在实践中，反缠绕策略(饱和度)可以添加到积分项中，或者可以使用更高阶的动作(例如PIN) 。对于安装相对噪声测量传感器的情况，通过将比例作用和积分作用分别放置在相邻agent之间的不同有向边上，PI策略可进一步开发为多层网络结构（Lombana&Di Bernardo，2016）。
备注 3. 在这篇简短的论文中，我们只考虑leader子系统和follwers子系统之间可能存在异质性，因此这些leaders在leader子系统中是同质的，并且只能具有不同的多项式系数，即沿着各自的移动轨迹。
备注4.实际上，这些差分项可能很难访问，并且应该设计相应的状态估计器来补偿控制性能。对于leaders来说，他们应该清楚自己的状态，比如当前的位置和对应的任意阶导数。因此，leaders不需要估计器，可以直接将他们的状态发送给邻居。对于第i个follower，我们定义了估计状态![\large z_i(t)=\left [ z_{i1}^T(t),z_{i2}^T(t),\cdots , z_{im}^T(t) \right ]](http://img.e-com-net.com/image/info8/85c02233a3564365a77ea05ba6b13319.gif){kind=small}
。此外，对于第i个领导者，它意味着：![\large z_i(t)=\left [ y_i^T(t),Dy_i^T(t),\cdots D^{m-1}y_i^T(t)\right ]](http://img.e-com-net.com/image/info8/4513c10e5b4b499388660e7eb215c524.gif){kind=small}
。然后，提出第i个follower的状态估计器为：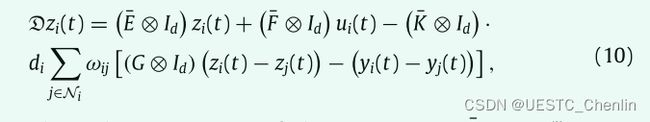
3.3 有时延的编队控制
假设网络内部存在非均匀时滞，编队控制问题将更加复杂。针对第i个follower提出了基于式(3) 的时滞仿射编队机动控制律：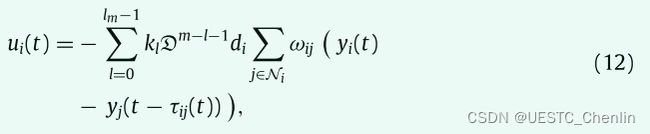
假设3：假设存在从agent-J到agent-I的时延
定理4：
备注5：
4.补充和仿真
2个仿真案例去验证我们的方法。
4.1 无时滞情况下仿射编队机动
在第一个例子中，三维空间中9个agent的立方标称编队(G，r)如图2所示。leader的数量满足4=d+1，它们的位置不共面，下面的G是4-rooted的。因此，满足假设1和假设2。我们可以得到一个具有特征值λ(Ls)={0、0、0、0、1、1、−0.5、4}和rank()=4的有符号拉普拉斯式。稳定矩阵D由Xu等人（2018）的算法1计算为diag（1、1、1、1、1、1、1、−1、1）。
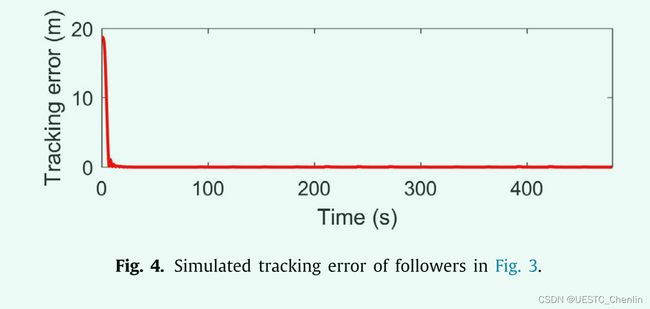
第一个示例的仿真结果如图3–4所示。为leaders选择五次多项式，因为每个轴上的一个五次多项式有六个系数，使它满足每个leader的初始和终止位置、速度和加速度的六个边界条件。如图3所示，立方编队通过仿射变换改变质心、尺度、旋转和其他几何图形去避障，如绕球圈，穿过狭窄的走廊。2-范数形式的跟踪误差可以快速收敛到零（如图4所示），并在整个机动过程中保持接近于零。
图3： 图2中的一个仿真示例说明了双积分followers在控制律(3)下跟踪五次多项式轨迹的时变仿射编队机动，其中K=[1.2500,5.4766,11.3723,14.2604,11.3723,5.4766]。为了便于查看，省略了线的箭头。
4.1 时滞情况下仿射编队机动
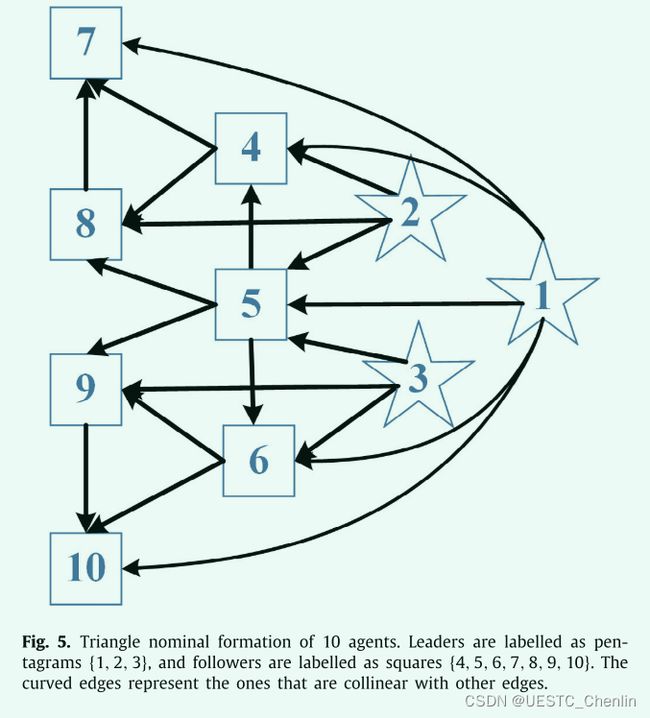
接下来，我们以10个agent的三角形标准队形编队进行第二个仿真示例，如图5所示。注意标准编队的队形不是几何的，因为存在共线agent，但三个leaders不共线 . 为每个边设置满足假设 3 的非均匀时变延迟，最大时间延迟为
，时间延迟的最大导数为 0.9。 由定理 3 计算的相应控制增益为 {3.0000, 13.1439, 27.2935, 34.2250, 27.2935, 13.1439}。 图6中agent的仿真编队可以从随机位置移动到共线形状。 跟踪误差收敛到零的速度相对较慢，并且在初始部分包含一个振荡周期，这是由非均匀延迟引起的。 给定相同的控制增益，如果选择较大的
，则无法进行任何机动。
5.总结
提出了一种基于有向图的仿射编队机动方法。我们的方法可以控制具有任意阶积分动力学的followers在任意维上成功地跟踪leaders的任意阶多项式轨迹。因此，可以连续实现质心、旋转、不同方向上的比例以及满足仿射变换的其他几何图案的时变编队机动。与赵（2018）提出的针对leader时变状态的加速度反馈要求相比，本文提出的控制律不需要高阶信息，并且节省了在设备上安装额外传感器的成本。由于时滞一直被认为是网络系统的固有特性，因此本文还针对现有的非均匀时变延迟设计了控制方案。这里我们列出了未来研究的几个重要课题。例如，本文提出的结果可以考虑复杂欠驱动动力学和运动约束。