【机器学习】笔记1:回归与误差分析
回归与误差分析
- regression
-
- step 1:model
- step 2:Goodness of Function
- step 3:Best Function(Gradient Descent)
-
- gradient descent
- selecting another model
- back to step 1
- back to step 2 : Regularization
-
- 测试结果
- 误差来源
-
- Variance
- Bias
- Bias VS variance
-
-
- 处理方法
-
- Modle Selection
regression
ML(机器学习)三个步骤:
- 寻找model,model就是function set(函数簇)
- 评估function set中每个function好坏(即函数簇选择不同的参数构成不同的函数)
- 找一个最好的function(即最好的一组参数)
回归任务的输出是一个数值(scalar)
step 1:model
model(function set):
y = b + ∑ w i x i y=b+\sum w_{i} x_{i} y=b+∑wixi
-
w(weights) 和 b(bias) 是参数,取不同值则构成不同function
-
xi(ferture): an attribute of input x
step 2:Goodness of Function
- 定义model(function set)
- 收集training data:(x,y^)
- 定义Loss Function L : function 的 function,衡量model中的每一个function的好坏,越低越好。
输入:一个function,输出:how bad it is
L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ∗ x c p n ) ) 2 \mathrm{L}(f)=\mathrm{L}(w, b) =\sum_{n=1}^{10}(\hat{y}^{n}-(b+w*x_{c p}^{n}))^{2} L(f)=L(w,b)=n=1∑10(y^n−(b+w∗xcpn))2
表示10个训练样本使用某个function(即某组w和b)的预测误差之和。
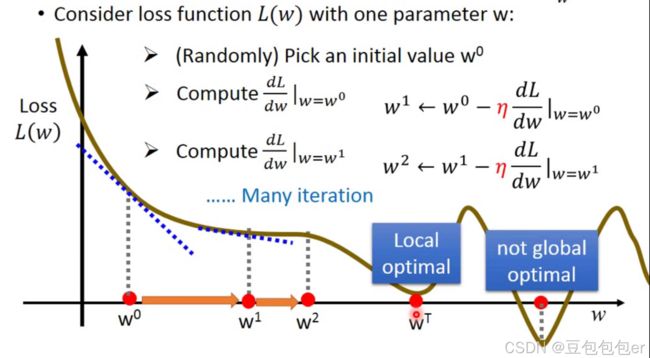
step 3:Best Function(Gradient Descent)
训练过程解决怎样从model(function set)中找到最佳的function,即如何找到最佳w,b
Pick the best function:
w ∗ , b ∗ = arg min w , b L ( w , b ) = arg min w , b ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 w^{*}, b^{*} = \arg \min _{w, b} L(w, b) \ = \arg \min _{w, b} \sum_{n = 1}^{10}\left(\hat{y}^{n}-\left(b+w \cdot x_{c p}^{n}\right)\right)^{2} w∗,b∗=argw,bminL(w,b) =argw,bminn=1∑10(y^n−(b+w⋅xcpn))2
gradient descent
微分为负数,表示需要向右更新参数,需要增大w,又因微分为负,所以前面要有 “-” 号。
selecting another model
我们更关心的是model在testing data中的error。引入高次项,尝试选取更复杂的modle。
低次式可以看做式高次式的子集,复杂的modle包含更多的function,所以对于同样的training data,复杂model error更低,拟合程度更高。但是复杂的model往往在testing data效果很差,即泛化能力很差,这种现象称为过拟合(overfitting)
back to step 1
考虑输入x的其他component,重新优化model
back to step 2 : Regularization
y = b + ∑ w i x i L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 y=b+\sum w_{i} x_{i} \\ \\ L=\sum_{n}\left(\hat{y}^{n}-\left(b+\sum w_{i} x_{i}\right)\right)^{2}+\lambda \sum\left(w_{i}\right)^{2} y=b+∑wixiL=n∑(y^n−(b+∑wixi))2+λ∑(wi)2
采用新的Loss Function,训练过程中我们追求更低的Loss。
-
前面一项为error,error越小代表function y越好;
-
后面一项表示function的smooth程度,参数值w越小代表function越平滑也越好
为什么选择平滑的function?
y = b + ∑ w i x i y=b+\sum w_{i} x_{i} y=b+∑wixi
当function y中参数值w越接近0,输出y随输入x的变化越不敏感,即该function越平滑。
平滑的function输出对输入不敏感,test过程中不易受到输入x噪声影响,从而可以输出更好的结果。
测试结果
λ越大,代表Loss函数中考虑function smooth的那一项影响力越大,我们更多考虑的是w本身的值,而减少考虑error,所以对于training data将得到比较大的error,但在testing data上面适当平滑的function对噪声不敏感,反而得到更佳的结果。
如何调节smooth程度,怎样选择λ?
误差来源
不同的model会得到不同的error,复杂model不一定error低
error来源:
- bias:估测function偏离真实function的程度
- variance(方差):同一个model不同training date得到多个预测function的松散程度
f ^ : 最 佳 ( 真 实 ) f u n c t i o n , 未 知 f ∗ : 一 次 实 验 根 据 t r a i n i n g d a t e 所 得 到 的 f u n c t i o n f ∗ 是 f ^ 的 估 测 值 \hat{f}:最佳(真实)function,未知 \\f^{*}:一次实验根据training\ date所得到的function \\f^{*}是\hat{f}的估测值 f^:最佳(真实)function,未知f∗:一次实验根据training date所得到的functionf∗是f^的估测值
Variance
不同training date 进行100次试验,发现简单model预测function接近,即variance小。复杂model预测function分散,variance大。
解释:越简单model对data的敏感程度越低。
Bias
同一model,不同training date 进行多次试验,得到很多预测function,再得到预测function的期望值。
E [ f ∗ ] = f ˉ E[f^{*}]=\bar{f} E[f∗]=fˉ
Bias定义:
B i a s : f ˉ 与 f ^ 的 接 近 程 度 Bias: \bar{f}与\hat{f}的接近程度 Bias:fˉ与f^的接近程度
- 黑色线为真实function
- 红色为每次training的预测function
- 蓝色为预测function的期望值
结果:
简单model虽然variance小,每次预测function都差不多,但是预测function的平均与真实function相差较大,即Bias很大。
复杂model虽然variance大,每次预测function差别很大,但是所有预测function的平均反而与真实function很接近,即Bias很小。
分析:
model即function set,简单model所包含function范围小,有可能不包含真实function,导致预测function的期望无法接近真实function,Bias很大;而越复杂的model所包含function范围越大,更容易sample出接近真实function的预测function,Bias小。
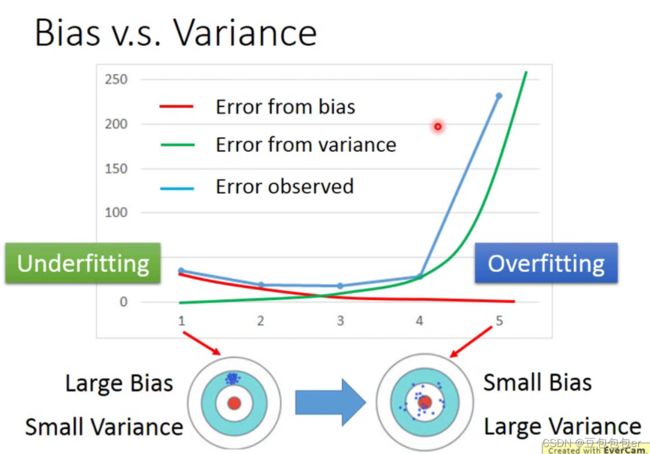
Bias VS variance
简单模型:Bias大,欠拟合(underfitting),甚至无法拟合training data
复杂模型:Varience大,过拟合(overfitting),training data error小,testing data error大
其实也很好理解
简单模型非线性效果差,拟合效果差,很有可能根本就无法满足对task的拟合,从根本上就“瞄不准”真实function,导致选取不同training data训练得到的预测function都距离真实function很远,导致Bias很大。尽管模型简单,对training data敏感度差,针对不同的training data都能预测出类似的预测function,使得variance小。
复杂模型的非线性能力就很强了,对于复杂的task,完全有能力“瞄准”task的真实function,多次对不同training data进行训练,得到不同的预测function都汇聚在真实function的周围。尽管复杂模型对training data敏感度强,针对不同的training data训练得到的每个预测function差别很大,即variance很大,但平均下来就很接近真实function了。
处理方法
1.bias大,欠拟合:
- 重新设计模型,输入x添加更多的feature
- 选择更复杂(高次)的model
2.variance大,过拟合:
- more data:training data更多,可以使得每次训练得到的预测function更加接近。假如进行100次训练,training data只有10个样本,每次选取10个不同的样本进行训练,得到100个预测function,它们每个差别都很大;但增加training data到100个样本,每次选取100个样本进行100次训练,这100个预测function就能够很接近。
- regularization:
使得模型能找到更平滑的function,LOSS function增加平滑模块,使得每个找到的预测function都更加平滑,所有曲线都集中在比较平滑的区域,更加汇聚,即variance变小。但人为改变了预测function,仅留下了平滑的部分,可能导致不包含真实function,Bias受损,这时候,调整平滑部分前面的weight就很重要了。
Modle Selection
我们想要bias和variance都很小的model
一个model训练后可能在自己的testing data效果还不错,但在真实应用场景可能很差,所以在training之后添加一个validation来验证不同模型的error,事先选择出error最小的model,之后再将这个模型应用于自己的testing data和真实应用场景,使得自己的testing data和真实应用场景的error差不多,及自己的testing performance 更能反映真实场景的performance。
将最初的training data分为training set和validation set:
- training set: 训练model,使用不同的model分别train出最优的预测function
- validation set:选model, 测试train出的不同的且最优的model在validation set中的performance
有时候我们使用训练完成的model对testing set进行测试,预测完成后,为了提升效果,再对model进行一些调整,使得model在testing set上拥有更好的效果。这实际上是人为地将testing set的 Bias考虑了进去,这样导致我们在testing set看到的performance没办法反映真实场景的performance。