xgboost论文详细介绍及翻译
XGboost:一种可扩展的boosting系统”论文介绍
摘要
作者介绍了一种可扩展的端到端tree boosting模型,这种模型能广泛应用于数据科学中,模型训练迅速,并能得到目前为止最好的实验结果。文章可分为两大部分,第一部分作者介绍了模型的原理,并提出了相应的算法;而第二部分主要讲系统的设计和实现。
第一部分中,作者介绍了模型的原理和推导,包括损失函数的构建、树分裂的原理等。为了有效的进行模型运算,作者提出了两种算法,一种为精确的朴素算法(Basic Exact Greedy Algorithm),而另一种为估计算法(Approximate Algorithm),这种算法能快速有效的进行分割点的查找,并能进行分布式的训练。在该估计算法下,作者还提出了对稀疏数据的解决方案(稀疏感知算法:Sparsity-aware algorithm)和一种能提出候选分割点的方法(加权分位草图:Weighted quantile sketch)。
第二部分中在系统设计与实现中,作者提出了三种可用于系统优化的方法:适用于并行学习的列块(Column Block for Parallel Learning)、自适应cache访问(Cache-aware Access)、核外计算的块(Blocks for Out-of-core Computation),而这三种方法也正是该系统能够可扩展(Scalable)的原因。
本文通过摘取和理解其中重要的部分,对该论文中的内容作出自己的解读和探讨。
一、模型的建立与推导
1.1正则化目标函数
由于XGboost是基于Tree Boosting的方法,因此作者首先简要地回顾了Tree Boosting的方法,并对其正则化目标函数做了微小的改进。
对于给出的数据集:![]()
其中n为数据集的个数;xi为第i条数据,且为m维向量;yi为第i条数据所对应的标签。
Boosting是集成学习的一种算法,其基本思想是将一族弱分类器提升为强学习器的算法。为了拟合数据集真实的分布,我们定义有K个弱分类器用于预测输出结果:

其中 y ^ \widehat{y} y i表示预测结果,fk代表第k个弱分类器,其结果为第k个弱分类器中xi映射到的那个叶子节点所具有的权值。其中F是fk的集合,又可以称为回归树(CART)空间,用数学符号表示为: ![]()
记该式为(1)式。
其中q为映射函数,其所表示的意义是将第i条数据xi映射到树的某个叶子节点;而T是叶子节点的个数;w所代表的含义是该叶子节点所具有的权重(原文中说wi代表第i个叶子节点具有的score,在这里将score理解为权值)。
当训练完所有的树模型以后,xi所对应的叶子节点已经确定,将所有对应的叶子权值求和,便可计算出预测结果。如下图所示。

预测出所有结果后,我们构建带由正则化项的损失函数,目标函数的抽象形式如下所示: 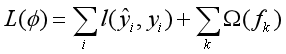
记该式为(2)式。
其中l为损失函数,其表现形式可以为MSE、交叉损失熵等。第二项Ω为正则化项,其具体作用是为了避免过拟合。其具体表现形式为:
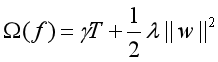
文章还指出,当正则化参数变为0时,就变为了一颗梯提升树。
PS:这貌似是由一个零范数和二范数组成的正则项,该操作在线性回归里也应该有应用。
1.2 Gradient Tree Boosting
在欧式空间中,形为式(2)的目标函数不能被传统的优化方法所优化。而GBDT提出了一种基于累加的方法训练该模型的方法。令 y ^ \widehat{y} y i(t)第t轮迭代、第i个实例所预测出的值,则根据(2)式,我们可以得到一个新的目标函数:
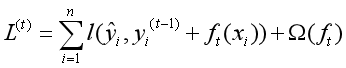
可以看到,l函数中的第二项变为了上一轮的预测结果加上ft,此处的ft代表本轮训练出的用于拟合上轮残差的一个模型(可理解为一个修正值)。
Friedman提出用损失函数的负梯度拟合t-1轮的残差,并用这个负梯度进行第t轮的训练。而此处作者认为ft(xi)可以视作一个微小量,因此对其进行了二阶泰勒展开。其具体结果为:

其中:
![]()
![]()
其中l( y y yi, y ^ \widehat{y} y i(t))是一个常数项,作者将其移除,得到第t轮迭代目标函数:

将该式记为(3)式。
此处可以将Ω代入,得到下式:
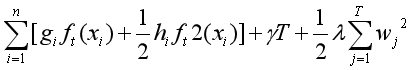
接下来是很关键的一步,为了求得最优的w值,我们定义:
![]()
其含义为叶子结点j所对应的数据集编号为i,全体i的集合为Ij。
那么(3)式就可以被改写为:
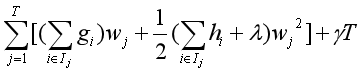
记该式为(4)式。
此处要做一些说明,其中T代表叶子节点有多少个,而ft(xi)的含义为第i条数据在t轮的预测结果,也就是叶子节点的权值。也就是说,原式表示的意思是,从第一条数据到第n条数据,一条一条的求和;而(4)式所代表的含义为:对每一个叶子节点上的数据进行求和,再对所有叶子节点进行求和。作者在论文中也给出了示例图,其中也用到了本文1.3中提到的结论,如下图所示:
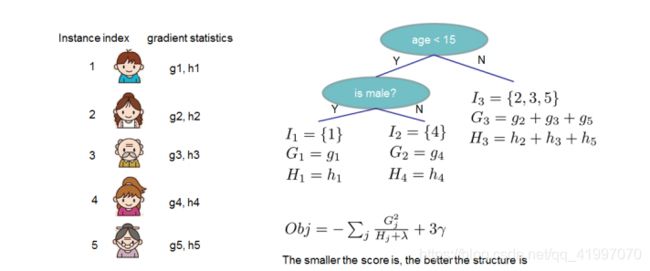
(4)式显然是一个抛物线形式的结构的式子,通过求其顶点,得到目标函数取到极值时wj的值,此时wj的值为:
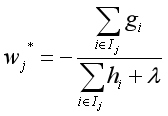
将该式记为(5)式。
此时目标函数的最优值为:

将该式记为(6)式。
此处的q代表第t轮CART的树的结构。
1.3 Basic Exact Greedy Algorithm
由此,作者提出了一种贪婪且精确的算法。这种算法将目标函数视为score,当且仅当其分裂后左子树和右子树的分数和,比原来节点的分数高时,树才开始分裂。用数学公式表示如下所示:
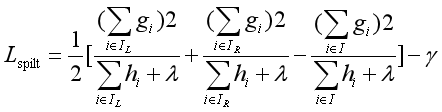
将该式记为(7)式。
其中I=IL∪IR。在实际算法操作中,由于γ是正则项系数,是一个常数,因此可以忽略γ。该公式用于在实际中判断出候选分割点,所谓候选分割点,我的理解是指按某个特征排序后可能用于树分裂的那个点。
该精确算法如下图所示:

1.4 Approximate Algorithm
除此之外,作者还提出了另外一种用于寻找候选分割点的估计算法,关于这两个算法的比较和为什么要提出这个算法这个问题,会放在1.5中进行解释。
总而言之,该估计算法首先根据特征的分布百分位(具体的解释会在下文加权分位草图部分中进行)提出候选分割点(candiate splitting points),然后根据候选分位点将特征映射到bucket中,最后从中找出最优的解。
在文章中,根据什么时候提出候选分割点,作者提出了该算法的两种变体。一种变体称之为global variant,global在最初的树的构造中,就提出了所有的候选分割点,并在每一层树的分裂时,都采用同一套候选分割点;另一种变体为local variant,local在每一次树分裂时,都会重新提出候选分割点。显然,local的方法会在提出分割点的时候更加有效。事实上,由于global提出的分割点是在每一层分裂都会用到的,因此他一开始需要提出的候选分割点比local的要多。
因此,现在关键的问题就是,如何通过特征分布来估计百分比分位点,从而提出候选分割点,作者因此提出了一种叫做weighted quantile sketch(加权分位草图)的方法。该方法如下所示。
对于原数据集衍生的数据集合Dk={(x1k,h1),(x2k,h2)…(xnk,hn)},其中xik代表第i条数据的第k个特征,hi表示二阶梯度。
定义排序函数:
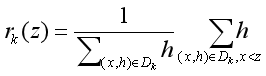
将该式记为(8)式。
其定义域为[0,+∞]。这代表了全体集合中,x比z小的数据总体的比例。
我们的目标是找出分位点集合{sk1,sk2…skl},使得:
![]() 将该式记为(9)式。
将该式记为(9)式。
这里的ε是一个估计因子,直观的来讲,大概会存在有1/ε个候选点。
这里数据集特征的分布是用二阶梯度衡量的,而作者也在论文中给出了为什么要用二阶梯度h衡量排序函数的原因:
将(3)式配方,得到:
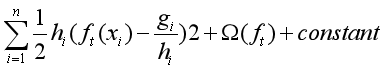
PS:原式是加号,我不知道为什么会变成减号,希望有人能告诉我。
这恰恰当标签为gi/hi时的加权平方损失。
1.5 Basic Exact Greedy Algorithm和Approximate Algorithm比较
精确算法(以下将1.3提到的算法均成为精确算法)对于提出候选分割点是非常有效的,其分割精度高,但是其也有非常明显的缺点,归纳如下:
①效率非常低下。
②不能用于分布式训练。
③当数据不能全部进入内存时,不能使用。
而估计算法虽然评价准确度较精确算法低,但是其可以用于分布式训练。
作者也在Higgs boson数据集中比较了两种算法,以及比较了local和global两种估计算法的变体,如下图所示。

从这张图也可以看出,当选取合适的eps时,精确算法和估计算法的效果是接近的。
1.6稀疏数据下的分割点寻找方法
在实际操作中,稀疏数据是一个非常重要的问题,造成数据稀疏的可能原因如下所示:
1)数据缺失。
2)统计意义上的0。
3)由于特征工程而出现的0,例如one-hot编码中出现的0。
为了解决在CART中出现的稀疏数据,XGboost提出了一种默认方向。文章认为,其最优的方向即为其默认方向。而最优的方向只由其不缺失的实体而计算得出。
PS:关于这部分,我的理解不够深入,希望有人能告诉我这部分具体是什么意思。
二、系统设计
在系统设计中,XGboost介绍了分布式结构的设计以及几种可以提高模型运行效率的方法。
2.1 适用于并行学习的Column Block
在XGBoost学习中,最影响效率的部分是将特征进行排序。为了减小排序造成的效率低下,文章提出了使用in-memory单元存储数据,称之为block。在每一个block中,数据都以compressed column(CSC)形式存储,每一个column都存储着对应的、已经排序好的一列特征(这也是为什么叫做column block的原因)。这个排序计算需要在训练之前完成。
在精确算法中,作者将数据集中的数据全部存储在一个block中,并且通过一次的线性扫描就可以统计所有的特征数据。
在估计算法中,column block可以分布在不同的机器中,每一个block对应了数据集的几行。使用这个已排序好的数据结构,百分位数寻找可以变成一个线性的复杂度。
2.2 Cache-aware Access
在block结构下,在计算候选分割点时,由于这些值已经在各个块中被有序排列,因此数据的访问不是直接通过行索引进行访问,这是一种不连续的内存访问,会造成读/写依赖。因此,作者提出了自适应缓存访问机制来解决这个办法。当梯度统计值(gradient statistics)在cache未命中时,或cache和内存速度不匹配时,cache-aware acess机制会自动的降低计算候选分割点的速度。
这种机制主要是由cache-aware prefetching算法实现的。具体的来说,该机制获取了每一个线程的缓存,并从缓存中提取了梯度统计信息,然后用mini-batch的方式进行累加。
2.3 核外计算的块(Blocks for Out-of-core Computation)
在以上的介绍中,该系统充分的利用了CPU资源、cache、内存,但是除此之外,为了最大效率地利用系统资源,作者还介绍了如何充分地利用硬盘空间,即核外计算的块如何进行优化的问题。
为了使得核外计算成为可能,首先我们将所有数据分成blocks并且将这些blocks存储在硬盘中。使用不独立的线程将block预取至内存缓冲区。但这么做仍然不够,因为这样做仍需要话费大量的I/O,因此作者介绍了两种可以用于提升核外计算速度的方法。
第一种方法叫做块压缩(Block Compression),即,用用某种压缩算法(文章中使用了General purpose compression algorithm)先压缩再解压以换取更小的空间,从而减小I/O时间。
第二种方法叫做块分片(Block Sharding),即,以一种可选择的方法将数据存放至不同的硬盘中,预取线程从每一个硬盘中取出数据到内存缓冲区中,而训练线程有选择地在每一个缓冲区中读取数据。这有助于提高硬盘读取的吞吐量。