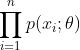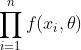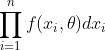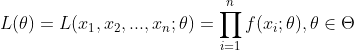基础数学系列(一)--似然函数与最大似然估计

1.似然函数

(1)离散型

若总体X属离散型,其分布律P{X=}=p(),的形式为已知,为待估参数,是可能取值的范围,设是来自X的样本,则的联合分布律为:

                                                                      .

又设是相应于样本的一个样本值,易知样本取到观测值的概率,亦即事件{}发生的概率为

                                                    

这一概率随的取值而变化,它是的函数,称为样本的似然函数(这里是已知的样本值,它们都是常数).

               那么我们可以作如下考虑:现在已经取到样本值了,这表明取到这一样本值的概率比较大,我们当然不会考虑那些不能使样本出现的作为的估计,再者,如果已知当时使取得很大值,而中其他值是取很小值,我们自然认为取作为未知参数的估计值较为合理.由费希尔引进的最大似然估计法,就是固定样本观察值,在取值的可能范围内挑选使似然函数达到最大的参数值,作为参数的估计值,即取使

                                                                 

这样得到的与样本值有关,记为,称为参数的最大似然估计值,而相应的统计量称为参数的最大似然估计量

(2)连续型

若总体X属连续型,其概率密度,的形式为已知,为待估参数,是可能取值的范围,设是来自X的样本,则的联合密度为:

                                                                                       

设是相应于样本的一个样本值,则随机点落在点()的邻域(边长分别为的n维立方体)内的概率近似地为

                                                                                       

这一概率随的取值而变化,它是的函数,但因子不随而变故只需考虑函数

                                                                                 

的最大值称为样本的似然函数,若

                                                                     

则称为参数的最大似然估计值,而相应的统计量称为参数的最大似然估计量 .

 

总结:已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值.最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值(利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值)