R语言实战——主成分分析理论推导与R语言实现
目录
- 1 总体主成分
-
- 1.1 主成分的定义与导出
- 1.2 主成分的性质
- 1.3 从相关矩阵出发求主成分
- 2 样本主成分
-
- 2.1 从S出发求主成分
- 2.2 从R出发求主成分
- 3 相关的R函数以及实例
-
- 3.1 `princomp`函数
- 3.2 `summary`函数
- 3.3 `loadings`函数
- 3.4 `predict`函数
- 3.5 `screeplot`函数
- 3.6 `biplot`函数
- 4 实例
- 附录——PCA高级散点图的绘制
- 补充说明
主成分分析(principal component analysis)是将多指标化为少数几个综合指标的一种统计分析方法,是由Pearson(1901)提出,后来被Hotelling(1933)发展了。主成分分析是一种通过降维技术把多个变量化成少数几个主成分的方法.这些主成分能够发映原始变量的绝大部分信息,它们通常表示为原始变量的线性组合.
1 总体主成分
1.1 主成分的定义与导出
1.2 主成分的性质
1.3 从相关矩阵出发求主成分
2 样本主成分
2.1 从S出发求主成分
2.2 从R出发求主成分
3 相关的R函数以及实例
下面介绍与主成分分析有关的函数:
3.1 princomp函数
作主成分分析最主要的函数是princomp()函数,其使用格式为:
princomp(formula, data = NULL, subset, na.action, ...)
其中formula是没有响应变量的公式(类似回归分析、方差分析,但无响应变量)。data是数据框(类似于回归分析、方差分析)。或者
princomp(x, cor = FALSE, scores = TRUE, covmat = NULL, subset = rep(TRUE, nrow(as.matrix(x))), ...)
其中x是用于主成分分析的数据,以数值矩阵或数据框的形式给出.cor是逻辑变量,当cor=TRUE表示用样本的相关矩阵R作主成分分析,当cor=FALSE(缺省值)表示用样本的协方差阵S作主成分分析。covmat是协方差阵,如果数据不用x提供,可由协方差阵提供.其他参数的意义见在线帮助.
prcomp()函数的意义与使用方法与princomp()函数相同.
3.2 summary函数
summary()与回归分析中的用法相同,其目的是提取主成分的信息,其作用格式为
summary(object, loadings = FALSE, cutoff = 0.1, ...)
其中object是由princomp()得到的对象。loadings是逻辑变量,当loadings=TRUE表示显示loadings的内容(具体含义在下面的loadings()函数),当loadings=FALSE则不显示.
3.3 loadings函数
loadings()函数是显示主成分分析或因子分析中loadings(载荷)的内容。在主成分分析中,该内容实际上是主成分对应的各列,即前面分析的正交矩阵Q。在因子分析中,其内容就是载荷因子矩阵。loadings()函数的使用格式为
loadings(x)
其中x是由函数princomp()或factanal()(见因子分析)得到的对象。
3.4 predict函数
predict()函数是预测主成分的值(类似于回归分析中的使用方法),其使用格式为
predict(object, newdata, ...)
其中object是由princomp()得到的对象.newdata是由预测值构成的数据框,当newdata缺省时,预测已有数据的主成分值.
3.5 screeplot函数
screeplot()函数是画出主成分的碎石图,其使用格式为
screeplot(x, npcs = min(10, length(x$sdev)), type=c("barplot", "lines"), main = deparse(substitute(x)), ...)
其中x是由princomp()得到的对象。npcs是画出的主成分的个数。type是描述画出的碎石图的类型,"barplot"是直方图类型,“lines"是直线图类型.
3.6 biplot函数
biplot()是画出数据关于主成分的散点图和原坐标在主成分下的方向,其使用格式为
biplot(x, choices=1:2, scale=1, pc.biplot=FALSE,...)
其中x是由princomp()得到的对象。choices是选择的主成分,缺省值是第1、第2主成分。pc.biplot是逻辑变量(缺省值为FALSE),当pc.biplot=TRUE,用Gabriel(1971)提出的画图方法.

4 实例
## 用相关矩阵做主成分分析,并显示分析结果
student.pr <- princomp(student, cor=TRUE)
summary(student.pr, loadings=TRUE) # 显示载荷矩阵
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.8817805 0.55980636 0.28179594 0.25711844 # R的特征值的开放
Proportion of Variance 0.8852745 0.07834579 0.01985224 0.01652747 # 方差贡献率
Cumulative Proportion 0.8852745 0.96362029 0.98347253 1.00000000 # 累计贡献率
Loadings: # R的特征向量
Comp.1 Comp.2 Comp.3 Comp.4
X1 0.497 0.543 0.450 0.506
X2 0.515 -0.210 0.462 -0.691
X3 0.481 -0.725 -0.175 0.461
X4 0.507 0.368 -0.744 -0.232
在上述程序中,语句student.pr<-princomp(student,cor=TRUE)可以改成student.pr<-princomp(~X1+x2+X3+X4,data=student,cor=TRUE),两者是等价的.
summary()函数列出了主成分分析的重要信息,
-
Standard deviation行表示的是主成分的标准差,即主成分的方差的开方,也就是相关阵的特征值 λ 1 \lambda_1 λ1, λ 2 \lambda_2 λ2, λ 3 \lambda_3 λ3, λ 4 \lambda_4 λ4的开方.
-
Proportion of Variance行表示的是方差的贡献率.
-
Cumulative Proportion行表示的是方差的累积贡献率.
第1主成分对应系数的符号都相同,其值在0.5左右,它反映了中学生身材魁梧程度:身体高大的学生,他的4个部分的尺寸都比较大,因此,第1主成分的值就较小(因为系数均为负值);而身材矮小的学生,他的4部分的尺寸都比较小,因此,第1主成分绝对值就较大.我们称第1主成分为大小因子.第2主成分是高度与围度的差,第2主成分值大的学生表明该学生“细高”,而第2主成分值越小的学生表明该学生“矮胖”,因此,称第2主成分为体形因子.
我们看一下各样本的主成分的值(用predict()函数).
## 查看主成分
predict(student.pr)
Comp.1 Comp.2 Comp.3 Comp.4
[1,] -0.06990950 -0.23813701 0.35509248 -0.266120139
[2,] -1.59526340 -0.71847399 -0.32813232 -0.118056646
[3,] 2.84793151 0.38956679 0.09731731 -0.279482487
[4,] -0.75996988 0.80604335 0.04945722 -0.162949298
[5,] 2.73966777 0.01718087 -0.36012615 0.358653044
[6,] -2.10583168 0.32284393 -0.18600422 -0.036456084
[7,] 1.42105591 -0.06053165 -0.21093321 -0.044223092
[8,] 0.82583977 -0.78102576 0.27557798 0.057288572
[9,] 0.93464402 -0.58469242 0.08814136 0.181037746
[10,] -2.36463820 -0.36532199 -0.08840476 0.045520127
[11,] -2.83741916 0.34875841 -0.03310423 -0.031146930
[12,] 2.60851224 0.21278728 0.33398037 0.210157574
[13,] 2.44253342 -0.16769496 0.46918095 -0.162987830
[14,] -1.86630669 0.05021384 -0.37720280 -0.358821916
[15,] -2.81347421 -0.31790107 0.03291329 -0.222035112
[16,] -0.06392983 0.20718448 -0.04334340 0.703533624
[17,] 1.55561022 -1.70439674 0.33126406 0.007551879
[18,] -1.07392251 -0.06763418 -0.02283648 0.048606680
[19,] 2.52174212 0.97274301 -0.12164633 -0.390667991
[20,] 2.14072377 0.02217881 -0.37410972 0.129548960
[21,] 0.79624422 0.16307887 -0.12781270 -0.294140762
[22,] -0.28708321 -0.35744666 0.03962116 0.080991989
[23,] 0.25151075 1.25555188 0.55617325 0.109068939
[24,] -2.05706032 0.78894494 0.26552109 0.388088643
[25,] 3.08596855 -0.05775318 -0.62110421 -0.218939612
[26,] 0.16367555 0.04317932 -0.24481850 0.560248997
[27,] -1.37265053 0.02220972 0.23378320 -0.257399715
[28,] -2.16097778 0.13733233 -0.35589739 0.093123683
[29,] -2.40434827 -0.48613137 0.16154441 -0.007914021
[30,] -0.50287468 0.14734317 0.20590831 -0.122078819
从第1主成分来看,较小的几个值是25号样本、3号样本和5号样本,因此说明这几个学生身材魁梧;而11号样本、15号样本和29号样本的的值较大,说明这几个学生身材瘦小.
从第2主成分来看,较大的几个值是23号样本、19号样本和4号样本,因此说明这几个学生属于“细高”型;而17号样本、8号样本和2号样本的的值较小,说明这几个学生身材属于“矮胖”型.
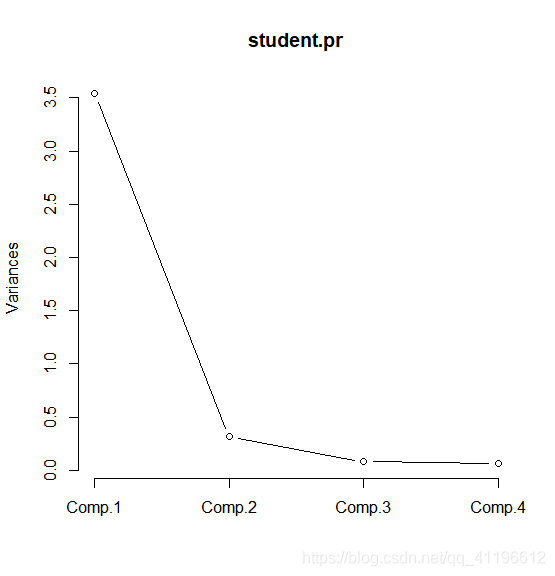
画出主成分的碎石图,参数选择直线型,可以换为直方图:
## 主成分的碎石图
screeplot(student.pr, type=c("lines"))
还可以画出关于第1主成分和第2主成分样本的散点图,其图形如下图所示.从该散点图可以很容易看出:哪些学生属于高大魁梧型,如25号学生,哪些学生属于身材瘦小型,如11号或15号;哪些学生属于“细高”型,如23号,哪些学生属于“矮胖”型,如17号.还有哪些学生属于正常体形,如26号,等等.
附录——PCA高级散点图的绘制
使用ggplot2绘制PCA散点图
分别利用颜色(colour)和形状(shape i.e. pch)进行分组很多属性需要单独设置。
用到的对象有
- 数据映射(Aes,Data aesthetic mappings)
- 几何属性(Geom,Geometric objects)
- 统计转换(Stat,Statistical transformations)
- 标度(Scales)
- 坐标系(xlab, ylab, coor, coordinate system)
- 主题(theme)
暂时未用到分面(faceting)
myData <- read.csv("data.csv")
myData2 <- myData[,-20]
myData3 <- na.omit(myData2)
pr<-prcomp(myData3[,5:20],scale=TRUE)
pca <- pr$x
####一下为ggplot2绘图
library(ggplot2)
pca <- as.data.frame(pca)
pca$salinity <- myData3$Salinity
pca$climate <- myData3$Climate
pca$ecotype <- myData3$Ecotype
pca$name <- myData3$Plant.name
theme<-theme(panel.background = element_blank(),
panel.border=element_rect(fill=NA),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
strip.background=element_blank(),
axis.text.x=element_text(colour="black"),
axis.text.y=element_text(colour="black"),
axis.ticks=element_line(colour="black"),
plot.margin=unit(c(1,1,1,1),"line"),
legend.title=element_blank(),
legend.key = element_rect(fill = "white")
)
percentage <- round(pr$sdev / sum(pr$sdev) * 100, 2)
percentage <- paste( colnames(pca), "(", paste( as.character(percentage), "%", ")", sep="") )
p <- ggplot(pca, aes(x=PC1, y=PC2,shape=paste(salinity, climate), colour=ecotype,label=name))
#p <- p + geom_point()+geom_text(size=3) + theme
p <- p + geom_point(size=3) +
theme +
xlab(percentage[1]) +
ylab(percentage[2]) +
scale_shape_manual(values = c(15,17,0,2),labels=c("Salt in Fanggan","Salt in Panjin","Fresh in Fanggan","Fresh in Panjin"))+
stat_ellipse(aes(shape = NULL))+
scale_x_continuous(limits = c(-6,6))+
scale_y_continuous(limits = c(-5,5.5))
p
结果:
补充说明
主成分分析是只能针对连续变量来进行压缩,分类变量则不行。 因为分类变量之间可以说是完全独立的,并没有正负两种相关性一说,如性别男和女之间就完全是独立的。如果一定也要将分类变量压缩的话,通常会对他们进行WOE转换,之后就可以愉快的进行压缩了。所以分类变量是没办法进行单独压缩的,因为没有对应的算法。有些人可能会直接对分类变量间进行卡方检验,然后把 p 值大的删去一些,这个其实应该被划分为手工的范畴,并不属于算法。