量子退火介绍
量子退火介绍
【所有内容均是对官方文档的学习记录总结】
本文介绍了量子退火是什么以及它是如何工作的,并介绍了量子退火所依赖的量子物理学相关知识点。
应用问题
量子退火处理器自然地返回低能量解决方案(return low-energy);一些应用程序需要真实的最小能量(优化问题),其他应用程序需要良好的低能量样本(概率抽样问题)。
优化问题:在优化问题中,我们需要从许多可能的组合中寻找最好的组合。物理学可以帮助解决这类问题,因为我们可以把这类问题定义为能量最小化问题。物理学的一个基本规则就是,任何事物都倾向于寻找一个最小能量状态。如,物体从山上滑下来;热的东西随着时间的推移而冷却下来。这种问题在量子物理中是存在的。简单来讲,量子退火就是利用量子物理寻找问题的低能态,从而找到最优或接近最优的元素组合。
采样问题:从低能态采样并表征能量形态(energy landscape)对我们想要构建 现实中的概率模型的 机器学习问题来说是非常有用的。样本为我们提供了关于给定参数集的模型状态的信息,然后用此来改善模型。
概率模型通过考虑我们知识中的差距和数据源中的错误来明确地处理不确定性。概率分布表示模型中未观测到的量和他们与数据之间的关系。数据的分布是基于有限样本集来近似的。该模型从观察到的数据进行推断,将观测数据之前定义的先验分布转换为在观测数据之后定义的后验分布,学习发生在这个转换期间。如果训练过程成功,学习的分布类似于生成数据的分布,允许对未观察到的数据进行预测。
从基于能量的分布中采样是属于计算密集型任务,这和D-Wave系统处理问题的方式非常匹配,也就是通过寻找低能态。
D-Wave系统中的量子退火机制
量子比特(qubits)是超导回路(superconducting loops)的最低能量状态,而超导回路是D-Wave QPU的组成部分。这些能量状态有循环电流和相应的磁场。(如图Figure2.1)同经典比特一样,qubit状态可以是0或1,但是因为qubit是量子对象,所以它同时是0态和1态的叠加态。在量子退火过程结束时,每个qubit从叠加态坍缩成0或1(经典状态)。
物理过程用能量图(energy diagram)可以可视化显示如图Figure2.2。这个图随时间变化,变化过程如图(a)(b)©。刚开始,只有一个山谷(valley),一个最小值**(a)。量子退火过程开始运行,障碍(barrier)开始提高,然后能量图就变成了双势阱(double-well potential)(b)**。此时,左谷的低点对应0态,右谷的低点代表1态。在退火结束时,qubit最终会出现在这些山谷中的一个。
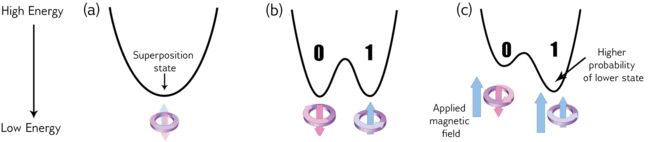
其他条件相等的情况下,qubit最终停在0态或者1态是等概率的。但是,我们可以通过给qubit施加一个额外的磁场来控制qubit处于0态还是1态的的概率**(c)**。这个磁场使得双势阱电位倾斜,增加了qubit在低阱中的概率。控制外加磁场的可编程的量叫做偏置(bias),qubit在偏置存在的情况下最小化能量。
不过单独的偏置项并没有作用。当把这些qubit连接在一起的时候,它们能够互相影响,qubit真正的能量就开始显现出来了,这是利用一种叫做耦合器(coupler)的设备来完成的。一个coupler可以使两个qubit趋向于同一种状态,即都是0 state或1 state ,或者coupler可以使它们趋向于相反的状态。就像一个qubit bias,耦合qubit之间的相关权重(weights)可以通过设置耦合强度来编程。总之,可编程biases(单个qubit所施加的外磁场)和weights(耦合量子比特之间的耦合权重)都是D-Wave系统中定义问题的方式。
当使用耦合器(coupler)的时候,我们使用的是另一种量子物理现象,被称为纠缠(entanglement)。当两个qubits发生纠缠时,它们可以被认为是拥有4种可能状态的单个物体。Figure 2.3 描述了这一思想,该图显示了一个有四种状态的势能,每种状态都相对应于两个qubit之间不同的组合:(0,0),(0,1),(1,1) and (1,0)。每个状态所对应的能量都决定于qubits之间的biases和coupling。在退火结束时,量子比特的状态最终会稳定在(1,1)的状态,在之前的退火过程中,qubit states 可能会在这个范围(landscape)是没有确定位置的(delocalized)。
如前所述,每个qubit有一个bias,并且qubits之间是通过couplers相互作用。在制定问题的时候,用户选择biases和couplers的值。偏置和耦合定义一个能量范围(The biases and couplings define an energy landscape),D-Wave计算机就是去寻找这个范围的最小能量:这就是量子退火。
量子比特越多,系统变得越来越复杂。有了两个量子比特,就有四种可能的状态来定义一个能量范围(energy landscape)。在三个量子位,我们有八个。对于添加的每一个量子位,可以定义 energy landscape 的状态数翻了一番:状态数随着量子位数的增加呈指数增长。
总结:从一组qubits开始,每一个qubit都是处于0态和1态的叠加态,还没有耦合。当在它们上面实现量子退火时,耦合(couplers)和偏置(biases)就被引入了,这时候qubits变得纠缠,在这一点上,系统处于许多可能答案的纠缠状态。到退火结束时,每个qubit都处在一个表示问题的最小能量状态的经典状态(classical state),或者是一个非常接近它的状态,发生在D-Wave系统中的这整个过程只需要几微秒的时间。
量子退火所依赖的物理学
哈密顿量(Hamiltonian)和本征谱(Eigenspectrum)
经典的Hamiltonian是对一些物理系统能量的数学描述。我们可以输入系统的任何特定状态,然后Hamiltonian返回的是那个状态的能量。对于大多数非凸Hamiltonians,寻找最小能量状态是一个经典计算机无法有效解决的NP-难问题。
举个例子,假如一个苹果和一张桌子构成一个简单的系统,系统只有两种可能的状态:苹果在桌子上,苹果在地面上。哈密顿量可以告诉我们能量,也就是平在桌子上这个状态的能量高于苹果在地面上这个状态的能量。
对于一个量子系统,Hamiltonian是一个把确定状态(本征态,eigenstates)映射为能量的函数。只有当系统处于Hamiltonian的本征态时,系统的能量定义为**本征能量。而当系统处于其他任何状态时,系统的能量都是不确定的。定义了本征能量的本征态的集合组成了本征谱**。
在D-Wave系统中,Hamiltonian 可以用如下式子表示:
H i s i n g = − A ( s ) 2 ( ∑ i σ ^ x ( i ) ) ⏟ Initial Hamiltonian + B ( s ) 2 ( ∑ i h i σ ^ z ( i ) + ∑ i > j J i , j σ ^ z ( i ) σ ^ z ( j ) ) ⏟ Final Hamiltonian (2.1) \displaystyle H_{ising}=\underbrace{-\frac{A(s)}{2}\left(\sum_{i}\hat\sigma_x^{(i)}\right)}_{\text{Initial Hamiltonian}} + \underbrace{\frac{B(s)}{2}\left(\sum_i h_i \hat\sigma_z^{(i)} + \sum_{i>j} J_{i,j} \hat\sigma_z^{(i)} \hat\sigma_z^{(j)}\right)}_{\text{Final Hamiltonian}} \tag {2.1} Hising=Initial Hamiltonian −2A(s)(i∑σ^x(i))+Final Hamiltonian 2B(s)(i∑hiσ^z(i)+i>j∑Ji,jσ^z(i)σ^z(j))(2.1)
其中 σ ^ x , z ( i ) \hat\sigma_{x,z}^{(i)} σ^x,z(i) 是量子比特 q i q_{i} qi 上的Pauli矩阵, h i h_i hi和 J i , j J_{i,j} Ji,j 分别是量子比特的偏置(qubit bias)和耦合权重(coupling strengths)
注: h i h_i hi和 J i , j J_{i,j} Ji,j 仅限于工作图(Chimara)中可用的值,Chimera后面会谈到。
Hamiltonian 是初始哈密顿量和最终哈密顿量两项的和。
- Initial Hamiltonian(first term)—— 当所有qubits 处在0和1的叠加态时初始哈密顿量的最低能量状态。这一项也称为 隧穿哈密顿量 (tunneling Hamiltonian)。
- Final Hamiltonian(second term)—— 终态Hamiltonian量的最低能量状态就是我们所解决问题的结果/答案。最终就是经典态,包含qubits偏置(bias)和qubits之间的耦合(coupling),这一项也称为问题哈密顿量 (problem Hamiltonian)
在量子退火中,我们从初始Hamiltonian 的最低能量本征态开始。随着退火的进行,引入包含 bias 和 couplers 的 problem Hamiltonian ,减小初始 Hamiltonian 的影响。在退火结束时,就处于 problem Hamiltonian 的本征态(eigenstate)。最理想的情况是,在量子退火过程中,始终都保持最小能量状态,所以到最后,仍然处于 problem Hamiltonian 的最小能量状态,就得到了想要的答案。退火结束之后,每个 qubit 都是classical object。
低能态退火
本征能量和时间的关系图是一种很有用的可视化量子退火过程的方式。退火过程中的最低能量状态(基态)通常显示在底部,其他任何较高的激发态都在上方。如图 Figure 2.4。
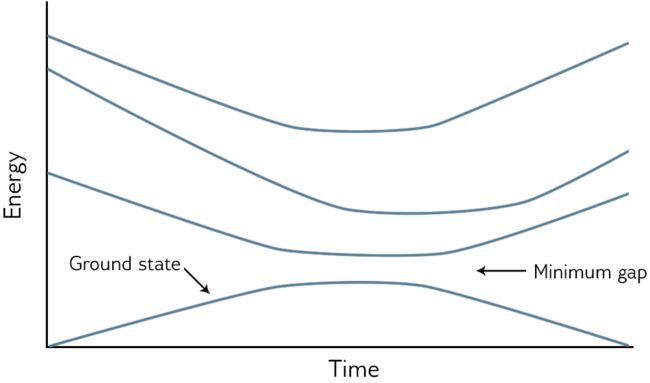
当退火开始时,系统以最低能量状态开始,该状态与任何其他能级很好地分开。随着问题哈密顿量的引入,其他能级可能会更加接近基态。它们越接近,系统从最低能量状态跳跃到其中一个激发状态的概率就越高。在退火过程中第一激发态(即除了基态外具有最低能量的激发态)有一个点会接近基态,然后再次发散。在整个退火过程中,基态和第一激发态之间的最小距离称为最小间隙(minimum gaps)。
某些因素会导致系统从基态跃迁到高能态,其中一个可能的因素就是物理系统的热波动,另一个原因就是退火过程太快。一种不受外部能源干扰,并能够足够缓慢的演化 Hamiltonian 的退火过程称为绝热过程(adiabatic process)。因为现实世界的计算不可能完全孤立运行,所以在理论上的理想状态是,量子退火的绝热量子计算可能被当成是真实世界的对立面(counterpart)。在现实中,对一些问题来说,停留在基态的可能性有时很小。不过,返回的低能态仍然很有用。
对于不同的特定问题,其 Hamiltonian 和对应的本征谱(eigenspectrum)都不同。对量子退火来说,最困难的问题通常是那些最小的 minimum gaps。
能量态的演化
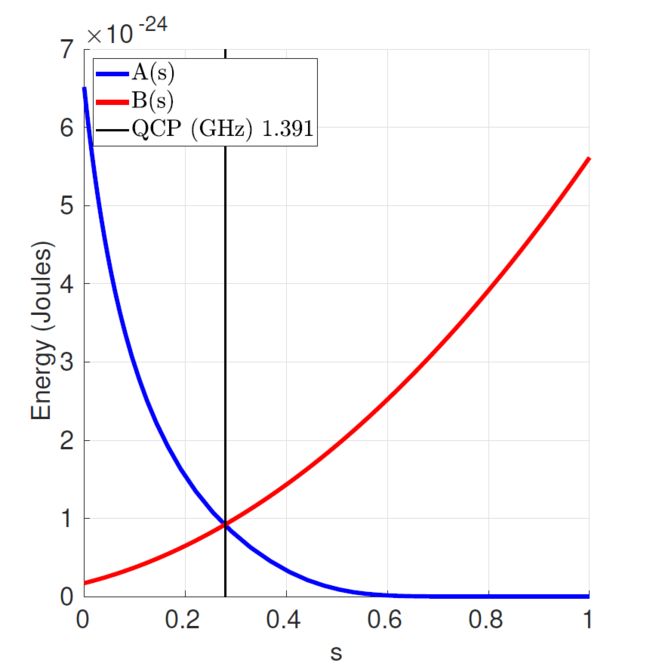
图2.5 显示了在物理温度不变的情况下,能量函数随时间变化的过程,此图以GHz为单位绘制了 E n e r g y h \frac{Energy}{h} hEnergy,其中 h h h 是普朗克常量( 6.6 × 1 0 − 34 6.6×10^{-34} 6.6×10−34 joule-seconds),归一化退火参数 s s s 是从0到1的抽象参数。曲线 A ( s ) A(s) A(s) 是退火能量,曲线 B ( s ) B(s) B(s) 是 s s s 上的 problem Hamiltonian 能量。线性退火集 s = t / t f s=t/t_f s=t/tf 其中 t t t 是时间变化量, t f t_f tf 是整个退火时间。在 t = 0 t=0 t=0 时刻, A ( 0 ) > > B ( 0 ) A(0)>>B(0) A(0)>>B(0) ,这就导致了量子系统的基态,该系统上的每个自旋都是经典态的离域组合(delocalized combination)。随着系统退火的进行, A A A 下降, B B B 上升到 t f t_f tf ,qubit 的终态就代表了低能量方案。
在退火结束之后,Hamiltonian 只包含 B ( s ) B(s) B(s) 项。这时就是一个经典 Hamiltonian,其中每个可能的经典比特串(即0或1的 qubit state 列表)对应一个本征态,并且本征能量就是我们要输入到系统中的经典能量目标函数。
