量子退火Python实战（2）：护士调度问题（NSP : Nurse Scheduling Problem）

---

前言：关于调度问题（Scheduling Problem）

调度就是人和机器的调度和排序。由于许多人的日程安排相互交织，还要考虑机器的运行状态等因素，实际业务中出现的日程安排极其复杂。

手动排程时，熟悉现场知识的老手通常要花几个小时来规划一个小规模的项目，甚至可能需要几天时间。但是，如果我们可以把这些问题建模成组合优化问题，这样便能在几分钟到几十分钟内自动设置复杂的调度。实际的工业界，有工人的工作时间调度和机器的使用时间调度。

• 护士调度问题（NSP）
  – 下面的论文里可知，NSP 从 1969 年之前就开始被研究，被认为是 NP-hard问题。作为现实生活中常见调度问题，我们会有很多约束，最主要的就是轮班约束和护士约束。本文将介绍护士调度问题中，一些常见约束如何建模为QUBO。

Solos, Ioannis; Tassopoulos, Ioannis; Beligiannis, Grigorios (21 May 2013). “A Generic Two-Phase Stochastic Variable Neighborhood Approach for Effectively Solving the Nurse Rostering Problem”. Algorithms. 6 (2): 278–308.doi:10.3390/a6020278.

---

一、护士调度问题（NSP）的QUBO建模

提示：本章参考了https://qard.is.tohoku.ac.jp/T-Wave/?p=1756，是日本东北大学专门研究量子退火研究室的学生写的量子退火的各种论文解析，这次解析的论文如下：

Title : Application of Quantum Annealing to Nurse Scheduling Problem Author : Kazuki Ikeda, Yuma Nakamura & Travis S.Humble Reference : Scientific Reports 9, Article number: 12837 (2019) https://doi.org/10.1038/s41598-019-49172-3

下面是一个简单的，4个护士，3个工作日的排班示例，我们称下面的表格为排班矩阵：

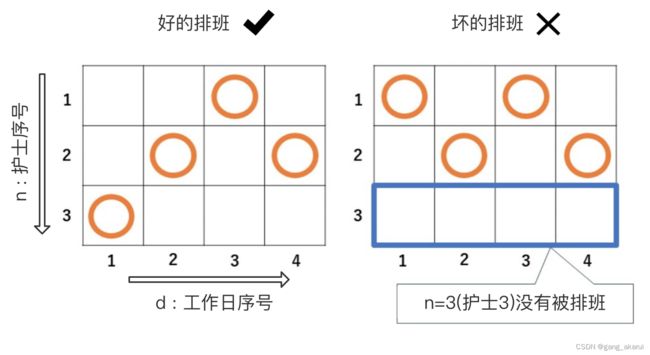
我们发现右边的排班，会导致护士3没有被安排工作，这是现实生活中不允许的，接下来讲目标变量和约束条件的建模。

1.目标变量

2.约束条件定义

因为护士调度问题不存在直接最小化的目标函数，只需要排班矩阵满足以下约束即可。

在 NSP 中可以想象各种约束示例。例如，可以完成的工作量（劳动力）取决于护士的经验。因此，在工作量大的日子里，不可能只有新人在一起工作。因此，我们需要【保证每天所需的劳动力】这一约束条件。可以考虑许多其他约束，但本文作为示例，定义了以下三个约束：

• 约束a. 确保没有护士连续工作超过 2 天（硬约束）
• 约束b. 确保每天都有所需的劳动力（硬约束）
• 约束c. 可以根据护士的忙碌程度调整上班的次数（软约束）

这里把约束分为硬约束和软约束。硬约束是必须满足的约束。另一方面，软约束是不必满足但需要满足的约束。

为了描述这些约束，需要的变量如下表所示：

★变量的注解：

• $F(n)$ ：为了保证每个人的最低出勤次数，$F(n)\ge rounddown(D/N)$;
  – rounddown()函数表示，向下取整。e.g. rounddown(3.6) = 3.
  – 例如，N=3,D=4，那么F(n) ≥ 1。就是说，每个护士4天里，必须工作一天以上。
• $h_1(n)$代表护士n的繁忙程度，取值及含义如下：
  – $h_1(n)=1(闲暇)$
  – $h_1(n)=2(普通)$
  – $h_1(n)=3(繁忙)$
• $h_2(d)$代表可出勤的时间带，取值及含义如下：
  – $h_2(d)=1(在工作日工作)$
  – $h_2(d)=2(周末或夜班)$

每个约束对应的QUBO项如下：

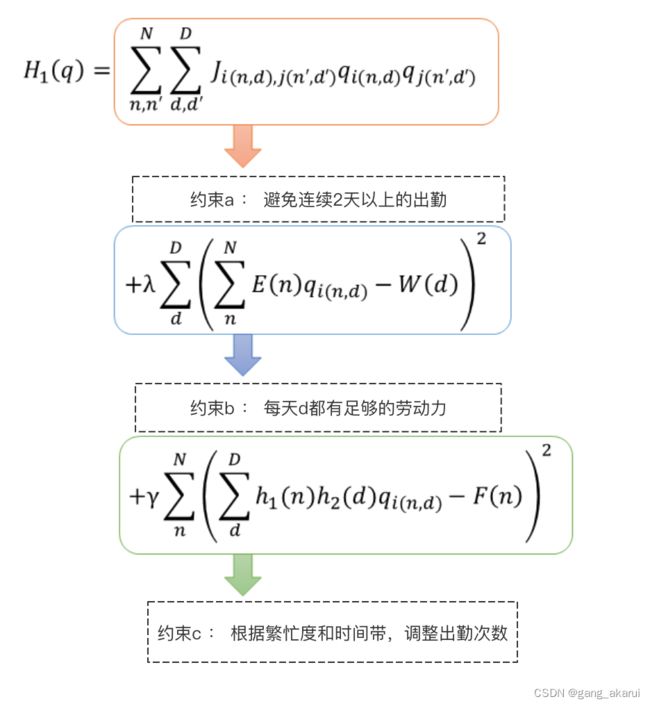
上面的约束全部满足的话，总哈密顿量$H_1(q)$的值为0。

3.【约束a】的补充说明

其实我们也可以不使用矩阵J来表示该约束，可以用下面的式子替代：

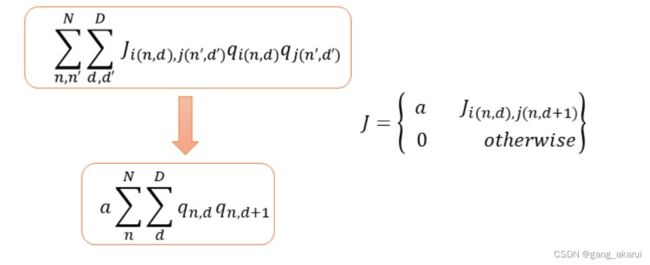
4.【约束c】的补充说明

约束c的$h_1$,$h_2$，通过下面的实例来帮助大家理解。

• N = 3
• D = 4
• $h_1$的具体值以及含义：
  – $h_1(1)=1(护士1闲暇)$
  – $h_1(2)=2(护士2普通)$
  – $h_1(3)=3(护士3繁忙)$
• $h_2(d)$
  – $h_2(d)=1(都希望，在工作日工作)$
• $F(n)=4(全员，每天都能工作)$

上面的具体值代入后：

• 护士1（闲暇）: ${\left({\sum }_d^D{q}_{i(1,d)}-4\right)}^2$ → 最多可以工作4天
• 护士2（普通）: ${\left({\sum }_d^{D}2q_{i(2,d)}-4\right)}^2$ → 最多可以工作2天
• 护士3（繁忙）: ${\left({\sum }_d^{D}3q_{i(3,d)}-4\right)}^2$ → 最多可以工作4/3天

通过该项，我们可以通过每个护士的繁忙程度来优化每个人的出勤时间。

二、Python实现NSP的QUBO

提示：本章参考了https://qard.is.tohoku.ac.jp/T-Wave/?p=2764，日本人经常会把实验结果可视化出来，值得借鉴。

1.参数设定表

因为NSP问题需要先设定一些参数的初始值，所以整理称表格如下：

from itertools import product
import numpy as np
from itertools import product
from pyqubo import Array, Constraint, Placeholder
from neal import SimulatedAnnealingSampler

N = 3  # 护士人数
D = 14  # 待排班日数
a = 7 / 2  # 连续工作2天以上的惩罚值
F = [4, 5, 5]  # 每个护士希望的出勤日数

2.QUBO实现

• 惩罚项矩阵$J$:

J = np.zeros((N, D, N, D))
for n1, d1, n2, d2 in product(range(N), range(D), range(N), range(D)):
    if n1 == n2 and d1 + 1 == d2:
        J[n1, d1, n2, d2] = a

• 总哈密顿量$H$

# binary变量
q = Array.create('q', shape=(N, D), vartype='BINARY')

# 连续工作2天以上的惩罚项矩阵
H1 = np.sum([J[n1, d1, n2, d2] * q[n1, d1] * q[n2, d2]
             for n1, n2, d1, d2 in product(range(N), range(N), range(D), range(D))])

# 确保每天d都有一个人的劳动力
H2 = np.sum([(np.sum([q[n,d] for n in range(N)]) - 1)**2 for d in range(D)])

# 确保全员出勤次数相等
H3 = np.sum([(np.sum([q[n,d] for d in range(D)]) - F[n])**2 for n in range(N)])

# 最小化的目标哈密顿量H
H = Placeholder('alpha') * Constraint(H1, 'H1') + Placeholder('lam') * Constraint(H2, 'H2') + Placeholder('gamma') * H3
model = H.compile()

• 退火算法采样

#这次采用neal的模拟退火
from neal import SimulatedAnnealingSampler
feed_dict = {'alpha': 1.0, 'lam': 1.3, 'gamma': 0.3} # 制約項の係数
bqm = model.to_bqm(feed_dict=feed_dict)
sampler = SimulatedAnnealingSampler()

# D-Wave的量子退火机可以这么使用
#from dwave.system import DWaveSampler, EmbeddingComposite
#sampler_config = {'solver': 'DW_2000Q_6', 'token': 'YOUR_TOKEN'}
#sampler = EmbeddingComposite(DWaveSampler(**sampler_config))

num_reads = 1000
sampleset = sampler.sample(bqm, num_reads=num_reads)
sampleset.record[:10]

输出结果如下：

• sampleset.record有以下几部分：
  – 解的状态
  – 能力值
  – 解的个数

rec.array([([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0], 4.76063633e-13, 1),
           ([0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1], 4.76063633e-13, 1),
           ([1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1], 4.68958206e-13, 1),
           ([0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0], 4.68958206e-13, 1),
           ([1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1], 4.68958206e-13, 1),
           ([0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0], 4.76063633e-13, 1),
           ([0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0], 4.68958206e-13, 1),
           ([0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1], 4.76063633e-13, 1),
           ([0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0], 4.76063633e-13, 1),
           ([0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0], 4.68958206e-13, 1)],
          dtype=[('sample', 'i1', (42,)), ('energy', '), ('num_occurrences', ')])

3.实验结果检验和可视化

检查解是否满足约束：

def extract_feasible_samples(samples, print_broken=False):
    feasible_samples = []
    for sample in decoded_samples:
        constraints = sample.constraints(only_broken=True)
        if len(constraints) == 0:
            feasible_samples.append(sample)
        elif print_broken:
            print(constraints)
    return feasible_samples

decoded_samples = model.decode_sampleset(sampleset.aggregate(), feed_dict)
feasible_samples = extract_feasible_samples(decoded_samples)
print('满足约束的解的个数：', len(feasible_samples))

输出结果：

满足约束的解的个数： 894

import matplotlib.pyplot as plt

lowest_sample = feasible_samples[0].sample

schedules = np.zeros((N, D))
for n in range(N):
    for d in range(D):
        if lowest_sample[f'q[{n}][{d}]'] == 1:
            schedules[n, d] = 1

plt.imshow(schedules, cmap="Greys")
plt.xlabel('D')
plt.ylabel('N')
plt.show()

打印出的结果如下：

print('实际的工作日数：', np.sum(schedules, axis=1))
print('希望的工作日数：', F)

实际的工作日数：[4. 5. 5.]
希望的工作日数：[4, 5, 5]

---

总结

重复实验的这位学生的最后总结如下：

令人失望的是，我无法为多达 56 个变量的问题找到一个好的基态解决方案。通过执行比本文更详细的系数搜索，精度有提高的余地，但随着排班日数的增加，它被认为几乎不可能解决。另一种提高准确性的方法是自己设置QUBO嵌入，但我不知道以我目前的知识做出什么样的嵌入。另外，这样的结果，我觉得很难投入实际使用，因为最多只能安排一个星期的班次。一旦我可以制定至少一个月的时间表，我想进行另一个实验。

其实，量子退火算法在QUBO建模上存在困难的同时，由于量子退火机和伊辛机还没有达到大规模实际问题的全结合bit数，所以，大家也要怀着谨慎的态度看待量子退火的未来。

下篇文章讲什么，还没有确定，有建议的可以留言给我。