论文笔记10：Denoising and Dimensionality Reduction Using Multilinear Tools for Hyperspectral Images

引言

高维数据空间大多是空的，表明所涉及的数据结构主要存在于子空间中。最流行的降维方法是主成分分析，它通过正交投影最大化数据方差。PCAdr的一个改进是独立成分分析(ICA)，它使用更高阶的统计量。但是，这两种降维方法需要初步的数据安排。事实上，在处理三向数据时，第一步是对所有图像进行矢量化，生成双向数据，允许使用信号处理，但忽略空间重排。

最大噪声分数，维纳和小波阈值，以及收缩都是有用的去噪技术。通常，混合方案包括通过主成分分析、傅立叶或离散余弦变换对每个去相关波段进行二维滤波的波段去相关。

我们的多线性代数方法同时降低了光谱维数，并以各种方式联合去噪。基于Tucker3分解，我们展示了低秩-$(K_1,K_2,K_3)$张量近似 [LRTA-$(K_1,K_2,K_3)$]作为去噪工具的能力。我们提出了一种新的方法，称为LRTA${}_{dr}$-$(K_1,K_2,D_3)$，它既执行空间低秩近似又执行光谱降维。

多向表示与性质

考虑三阶张量$\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$，元素为$x_{i_1{i}_2{i}_3}$，其中$i_1=1,\cdots ,I_1$，以此类推，$\mathbb{R}$为实流形，每个索引(index)称为way或mode，n模向量为$I_n$维，由张量通过改变指标$i_n$而保持其他指标不变得到。$\mathcal{X}$的n模展平矩阵${\mathbf{X}}_n$的列均为n模向量。HSI数据可以表示为一个三维数组或三阶张量：行和列的两个方向和光谱波段的一个方向。

$\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$的n模秩定义为$Ran{k}_n(\mathcal{X})$，即$I_n$维向量(n模向量)张成的向量空间的维度，$\mathcal{X}$称为一个rank-$(K_1,K_2,K_3)$张量如果$Ran{k}_n(\mathcal{X})=K_n$.

去噪工具：LRTA-$(K_1,K_2,K_3)$

根据Tucker3模型，任何三维数据$\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$可分解为
$$\mathcal{X}=\mathcal{C}{\times }_1{\mathbf{U}}^{(1)}{\times }_2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}$$

其中${\mathbf{U}}^{(n)}$为正交n-模矩阵，包含与展平矩阵${\mathbf{X}}_n$的$K_n$个最大特征值相关的$K_n$个特征向量，$\mathcal{C}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$为core张量，类似于传统矩阵奇异值分解中的对角奇异值矩阵，${\times }_n$为n-模积。

给定一个实值三维数据$\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$，LRTA-$(K_1,K_2,K_3)$的目的是寻找更低秩–$(K_1,K_2,K_3)$多向数据$\hat{\mathcal{X}}$，$K_n<I_n$，$n=1,2,3$，最小化quadratic Frobenius范数：$\Vert \mathcal{X}-\hat{\mathcal{X}}{\Vert }_F^2$. $\mathcal{X}$的最佳更低秩-$(K_1,K_2,K_3)$多向近似表述为
$$\mathcal{X}=\mathcal{X}{\times }_1{\mathbf{P}}^{(1)}{\times }_2{\mathbf{P}}^{(2)}{\times }_3{\mathbf{P}}^{(3)}$$

其中${\mathbf{P}}^{(n)}={\mathbf{U}}^{(n)}{{\mathbf{U}}^{(n)}}^T$，${\mathbf{P}}^{(n)}$是经过交替最小二乘(ALS)算法收敛后得到的，由于这个过程，沿着给定模式的任何projector都依赖于沿着所有其他模式的projector.

加性噪声也可以表示为一个三向数组$\mathcal{N}$，因此观测的HSI数据可以表示为$\mathcal{R}=\mathcal{X}+\mathcal{N}$，$\mathcal{R},\mathcal{X},\mathcal{N}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$，我们使用基于子空间的方法估计张量$\mathcal{X}$. 在二维信号处理中，这些方法使用由与观测向量组的协方差矩阵的最大特征值相关联的特征向量所跨越的信号子空间。同样，当噪声$\mathcal{N}$与信号张量$\mathcal{X}$不相关时，通过假设不管n-模是什么，$E^{(n)}$是维数为$K_n$的信号子空间$E_{ss}^{(n)}$和维数为$I_n-K_n$的噪声正交子空间$E_{ns}^{(n)}$的直接(direct)和，经典的子空间方法可以扩展到多向数据。

在张量公式中，通过计算LRTA-$(K_1,K_2,K_3)$来确定n-模向量空间上的投影。从含噪张量$\mathcal{R}$中估计信号张量$\mathcal{X}$的一个方法是在$\mathcal{R}$的每个n-模中估计$E_{ss}^{(n)}$，并将$\mathcal{R}$的每个n-模向量正交投影到n-模信号子空间$E_{ss}^{(n)}$上，$n=1,2,3$. LRTA-$(K_1,K_2,K_3)$允许对于每一个n-模，只保留与n-模展平矩阵${\mathbf{R}}^n$的$K_n$个最大特征值相关的$K_n$个特征向量。这个声明可以写成
$$\mathcal{X}=\mathcal{R}{\times }_1{\mathbf{P}}^{(1)}{\times }_2{\mathbf{P}}^{(2)}{\times }_3{\mathbf{P}}^{(3)}$$

其中${\mathbf{P}}^{(n)}={\mathbf{U}}^{(n)}{{\mathbf{U}}^{(n)}}^T$，${\mathbf{U}}^{(n)}=[{\mathbf{u}}_1,\cdots ,{\mathbf{u}}_{K_n}]$为n-模信号子空间上的投影。为了估计信号子空间维数$K_n$，扩展了著名的的Akaike信息准则(AIC)。这种多向数据分析的主要问题是利用ALS算法联合空间和光谱信息去除噪声。

降维工具：LRTA${}_{dr}$-$(K_1,K_2,D_3)$

我们有兴趣通过选择更重要的光谱特征来减少光谱波段的数量，以改进分类。$I_3$张大小为$I_1\times I_2$的图像，通过行连接(concatenation)，每个图像被转换成一个向量。数据张量$\mathcal{R}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$变为矩阵$\mathbf{R}\in {\mathbb{R}}^{I_3\times p}$，其中$p=I_1\times I_2$. 降维的目的是提取少量$D_3<I_3$的特征，称为PCs，因此，$D_3$PCs生成一个reducing矩阵$\mathbf{Z}\in {\mathbb{R}}^{D_3\times p}$
$$\mathbf{Z}=\mathbf{R}\times {\Lambda }^{-1/2}{\mathbf{U}}^{\mathrm{T}}$$

数据可以被重新reshaped为一个三向数组$\mathcal{Z}\in {\mathbb{R}}^{I_1\times I_2\times D_3}$. 先前获得的矩阵$\mathbf{R}$等价于$\mathcal{R}$的三模展平矩阵，记为${\mathbf{R}}_3$. 然后，上式可以写为
$$\mathcal{Z}=\mathcal{R}{\times }_3{\mathbf{\Lambda }}^{-1/2}{\mathbf{U}}^{(3{)}^{\mathrm{T}}}$$

同样的，我们可以把LRTA-$(K_1,K_2,K_3)$变成光谱DR工具，称为LRTA${}_{dr}$-$(K_1,K_2,D_3)$，其中$D_3$代表光谱PCs的数量。由于LRTA${}_{dr}$-$(K_1,K_2,D_3)$是联合降低光谱模式的维数并将信息沿着空间模式投影到较低的$(K_1,K_2)$-维的子空间上，所以执行该挑战。后一种处理允许对数据进行压缩和空间去噪。对于每种模式，可以保留不同的参数值$(K_1,K_2,D_3)$. LRTA${}_{dr}$-$(K_1,K_2,D_3)$模型为
$$\mathcal{Z}=\mathcal{R}{\times }_1{\mathbf{P}}^{(1)}{\times }_2{\mathbf{P}}^{(2)}{\times }_3{\mathbf{\Lambda }}^{-1/2}{\mathbf{U}}^{(3{)}^{\mathrm{T}}}$$

其中，$U^{(3)}$是包含$D_3$个选定特征向量的矩阵，$\mathbf{\Lambda }$是包含$D_3$个最大特征值的对角特征值矩阵，而$P^{(n)}$是n-模的投影。

首先，LRTA${}_{dr}$-$(K_1,K_2,D_3)$联合使用空间和光谱信息来提取光谱PCs。其次，由于估计的空间投影$P^{(n)},n=1,2$，LRTA${}_{dr}$-$(K_1,K_2,D_3)$对提取的光谱PCs进行去噪。迭代ALS算法允许人们考虑NR和DR之间的交叉相关性。

实验

实验数据：${\mathcal{R}}^{310\times 220\times 148}$，预处理步骤去除初始多向数据$\mathcal{R}$的每个矢量像素的平均值。

分类是通过SAM算法进行的，评估指标：总准确率OA，对于P类$C_i,i=1,\cdots ,P$，$a_{ij}$定义为实际上属于$C_i$类却被划分到$C_j$类的测试样本的个数，$i,j=1,\cdots ,P$，则OA定义为$\mathrm{O}\mathrm{A}=\frac{1}{M}{\sum }_{i=1}^P{a}_{ii}.$ 其中$M$为样本总数。

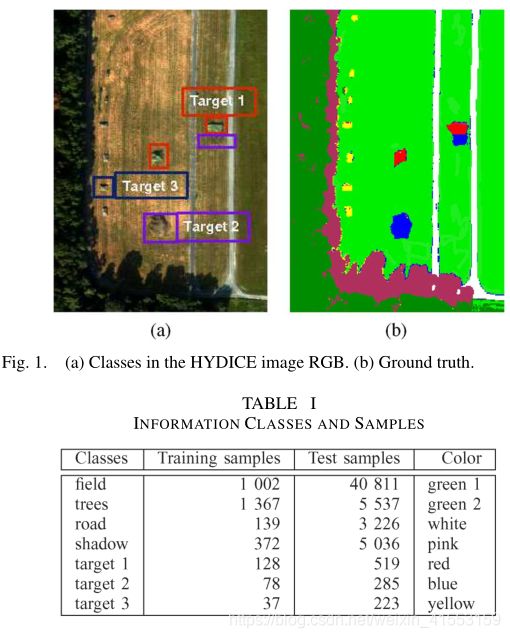
无降维的分类

该实验评估了对真实数据去噪以改善分类结果的必要性，LRTA-$(K_1,K_2,K_3)$的$(K_1,K_2,K_3)$值由AIC估计。对于本实验，$(K_1,K_2,K_3)$值估计为(100，100，80).

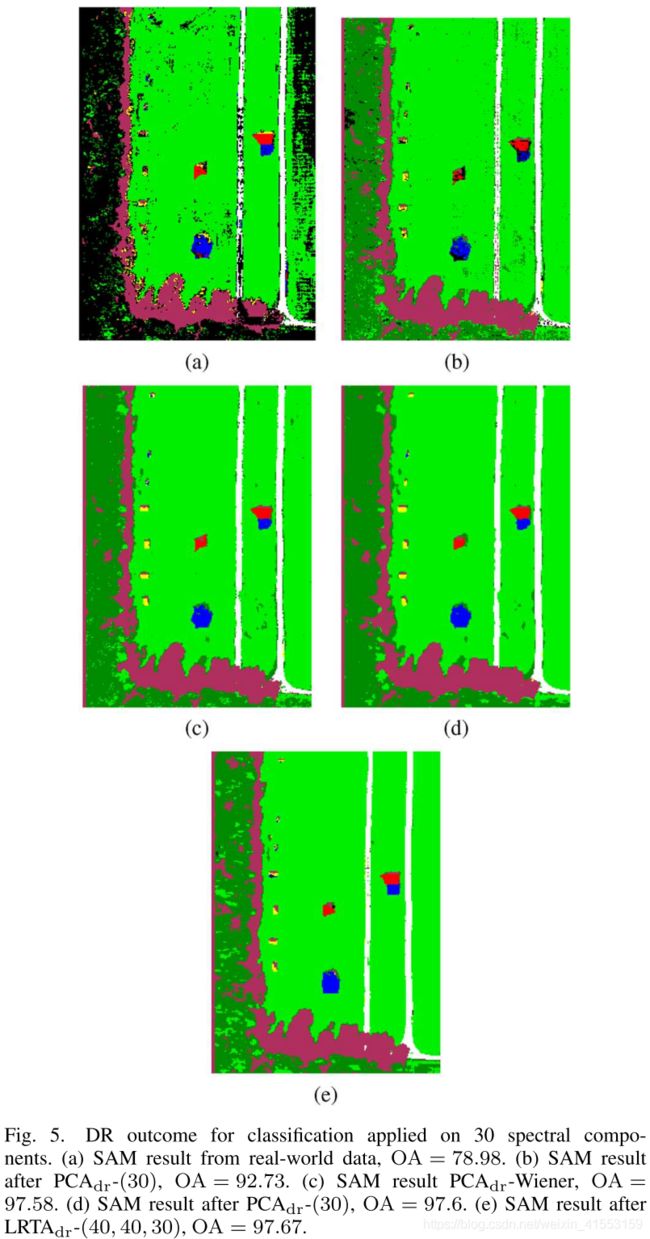
分类结果中出现的黑色像素代表未分类的像素。我们从视觉结果和OA值中注意到去噪是一个必要的预处理步骤。对于这个真实世界的数据，LRTA-$(K_1,K_2,K_3)$优于比较的方法。

有降维的分类

保留的光谱特征的数量对分类效率有影响，对于$D_3$的每个值，$(K_1,K_2)$值越低，分类结果越好。

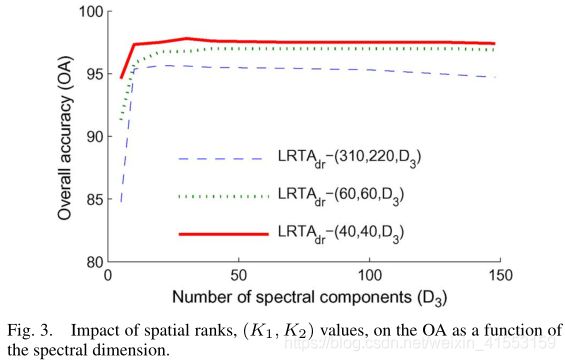
对于PCA${}_{dr}$方法，我们注意到有一个最佳的光谱维数。LRTA${}_{dr}$-$(K_1,K_2,D_3)$在所有$D_3$值下都比PCA${}_{dr}$-($D_3$)产生更好的OA.

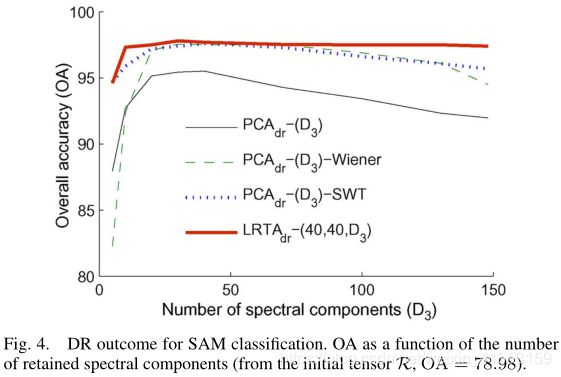
LRTA${}_{dr}$-$(40,40,30)$允许同时降低光谱维数和空间维数，这对于SAM分类器是非常重要的。

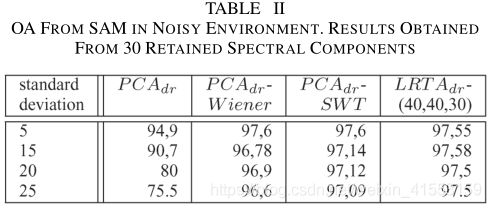
有噪声环境下分类

改进之处：

代码(matlab)

function [X, Z, K] = LRTA(Y) % addpath 'D:\kp_matlab\tensor dictionary learning\tdl_demo\compete_methods'

%==========================================================================
% Implements the lower rank tensor approximation (LRTA) for MSI [1].
%
% Syntax:
%   [X, Z, K] = LRTA(Y);
%
% Input:
%   Y - the I1 x I2 x I3 noisy imagery tensor
%   
% Output:
%   X - the denoised imagery tensor whose size is equal to Y's
%   Z - the I1 x I2 x D3 reducing tensor after DR
%   K - estimated n-rank of the imagery
%
% [1] N. Renard, S. Bourennane, and J. Blanc-Talon, "Denoising and
%     Dimensionality Reduction Using Multilinear Tools for Hyperspectral
%     Images", IEEE Geoscience and Remote Sensing Letters, vol. 5, no. 2,
%     Apr. 2008.
%
% by Yi Peng
%==========================================================================

typename = class(Y); % 返回对象的数据类型
addpath 'D:\kp_matlab\tensor dictionary learning\tensor_dl\dependency\tensor_toolbox'
if ~strcmp(typename, 'tensor') % 用于做字符串比较的函数
    Y = tensor(Y); % creates a tensor from the multidimensional array Y, using SIZ = size(Y).
end
I = size(Y);
if numel(I) == 2 % 二维图像
    I(3) = 1;
end

% remove the average of each band
Yflat = double(tenmat(Y, 3)); % tenmat函数将张量存储为矩阵形式,也就是张量展开成矩阵,I(3)*[I(1)*I(2)]
bandwise_avg = mean(Yflat, 2); % 对每一行求平均
Y = Y - reshape(repmat(bandwise_avg, [1, I(1)*I(2)])', I); % repmat将bandwise_avg复制成1*(I(1)*I(2))

% estimate K1, K2 and K3
K = zeros(1, 3);
addpath 'D:\kp_matlab\tensor dictionary learning\tensor_dl\utils'
for k = 1:3
    Yflat = double(tenmat(Y, k));
    AICscore = DimDetectAIC(Yflat'); % 调用DimDetectAIC函数，返回size(Yflat',2)-1维向量
    [~, K(k)] = min(AICscore); % 返回索引
end

% denoising via LRTA
X = tucker_als(Y, K, 'init', 'nvecs', 'tol', 1e-8, 'printitn', 0); % 调用tucker_als函数

% perform DR to improve classification performance
Z = ttm(X.core, X.U, -3); % ktensor、@tensor、@ttensor里面都有ttm

X = tensor(X) + reshape(repmat(bandwise_avg, [1, I(1)*I(2)])', I); % add the average of each band

代码测试结果：