Pipeline机器学习模型串联

机器学习模型训练时使用 Pipeline 是一个加快效率的串联方法。Pipeline 处理机制就像是把所有模型塞到一个管子里，然后依次对数据进行处理，得到最终的分类结果。

# 模型串联
pip=Pipeline(
              [                                # 所有模型写进列表内
                （‘模型一名称’,模型一调用）,    # 模型名称可自定义
                （‘模型二名称’,模型二调用）,
                （‘模型三名称’, 模型三调用）
              ]
            )

# 模型调用
model=pip.fit(x,y)

Pipeline 函数可以把多个模型按顺序打包在一起，输入的数据集经过模型的处理后，输出的结果作为下一步的输入，最后一步的估计器对数据进行分类或者其他处理。除了最后一个模型外，其他模型都必须实现 "fit()" 和 "transform()" 方法， 最后一个模型需要实现 fit() 方法即可。当训练样本数据送进 pip 进行处理时， 逐个调用模型的 fit() 和 transform() 方法，用最后一个模型的 fit() 方法分类或者其他处理。

示例代码：

import pylab as pl
from sklearn import datasets
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

digits=datasets.load_digits()

# 数据可视化
pl.gray() # 灰度化图片
pl.figure(figsize=(3, 3))
pl.matshow(digits.images[1])  # 显示图片
pl.show()

x_train, x_test, y_train, y_test = train_test_split(digits.data, digits.target, test_size=0.25, random_state=33)

pip = Pipeline([('sc', StandardScaler()), ('svc', LinearSVC())])

pip.fit(x_train, y_train)
y_predict = pip.predict

print(pip.score(x_test, y_test))
names = digits.target_names
print(classification_report(y_test, y_predict, target_names=names.astype(str)))

模型误差 = 偏差 + 方差 + 不可避免的误差（噪音）。

通常随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小

偏差衡量了模型的预测值与实际值之间的偏离关系。例如某模型的准确度为96%，则说明是低偏差；如果准确度只有70%，则说明是高偏差。

方差描述的是训练数据在不同迭代阶段的训练模型中，预测值的变化波动情况（或称之为离散情况）。从数学角度看，可理解为每个预测值与预测均值差的平方和的再求平均数。通常在模型训练中，初始阶段模型复杂度不高，为低方差；随着训练量加大，模型逐步拟合训练数据，复杂度开始变高，此时方差会逐渐变高。

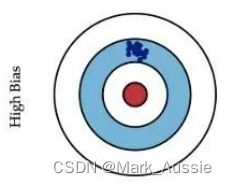
如上左图，目标是中心的红点，所有的预测值都偏离了目标位置，这就是偏差；

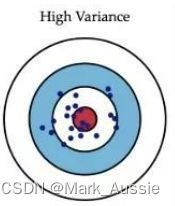
如上右图，预测值围绕着红色中心周围，没有大的偏差，但是整体太分散了，不集中是方差；

• 低偏差，低方差：理想模型，蓝色点落在靶心范围，数据离散程度小，基本在靶心范围内；
• 低偏差，高方差：过拟合。泛化（或通用）能力差；
• 高偏差，低方差：通常为训练的初始阶段；
• 高偏差，高方差：训练最糟糕的情况，准确度差，数据的离散程度也差。

模型有偏差，可能是问题本身的假设是不正确的，或者欠拟合。如：针对非线性的问题使用线性回归；或者采用的特征和问题完全没有关系，如用学生姓名预测考试成绩，就会导致高偏差。

方差表现为数据扰动很大影响模型。即模型没有完全学习到问题的本质，而学习到很多噪音。可能是使用的模型太复杂，如：使用高阶多项式回归，就是过拟合。

一些算法天生就是高方差的算法，如KNN算法。非参数学习算法通常都是高方差，因为不对数据进行任何假设。一些算法天生就是高偏差算法，如线性回归，参数学习算法通常都是高偏差算法。

偏差和方差通常是矛盾的。降低偏差，会提高方差；降低方差，会提高偏差。这就需要在偏差和方差之间保持一个平衡。以多项式回归模型为例，可以选择不同的多项式的次数，来观察多项式次数对模型偏差和方差的影响。

参考：

机器学习第六周--机器学习重要概念补充 - Mindy-snail - 博客园 (cnblogs.com)