深度学习入门（二） 环境配置与预备知识

前言

核心内容来自博客链接
希望大家多多支持作者
本文记录用，防止遗忘

环境配置与预备知识

一 环境配置

Anaconda

Anaconda是Python的一个开源发行版本，主要面向科学计算。我们可以简单理解为，Anaconda是一个预装了很多我们用的到或用不到的第三方库的Python。而且相比于大家熟悉的pip install命令，Anaconda中增加了conda install命令。当你熟悉了Anaconda以后会发现，conda install会比pip install更方便一些。
总的来说，我们应该完成以下几步：

1、根据操作系统下载并安装Anaconda（或者mini版本Miniconda）并学会常用的几个conda命令，例如如何管理python环境、如何安装卸载包等；
2、Anaconda安装成功之后，我们需要修改其包管理镜像为国内源，这样以后安装包时就会快一些。

Jupyter

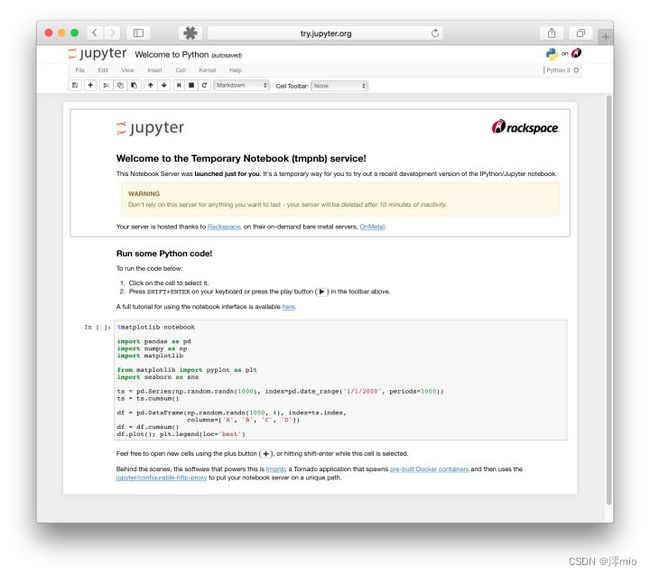
在没有notebook之前，在IT领域是这样工作的：在普通的 Python shell 或者在IDE（集成开发环境）如Pycharm中写代码，然后在word中写文档来说明你的项目。这个过程很繁琐，通常是写完代码，再写文档的时候我还的重头回顾一遍代码。最蛋疼的地方在于，有些数据分析的中间结果，还得重新跑代码，然后把结果弄到文档里给客户看。有了notebook之后，世界突然美好了许多，因为notebook可以直接在代码旁写出叙述性文档，而不是另外编写单独的文档。也就是它可以能将代码、文档等这一切集中到一处，让用户一目了然。如下图所示。

PyTorch

由于本文需要用到PyTorch框架，所以还需要安装PyTorch（后期必不可少地会使用GPU，所以安装GPU版本的）。直接去PyTorch官网找到自己的软硬件对应的安装命令即可

其他

此外还可以安装python最好用的IDE PyCharm
如果不喜欢用IDE也可以选择编辑器，例如VSCode等。

二 数据操作

在深度学习中，我们通常会频繁地对数据进行操作。作为动手学深度学习的基础，本节将介绍如何对内存中的数据进行操作。
为了能够完成各种数据操作，我们需要某种方法来存储和操作数据。通常，我们需要做两件重要的事：（1）获取数据；（2）将数据读入计算机后对其进行处理。 如果没有某种方法来存储数据，那么获取数据是没有意义的。

在PyTorch中，torch.Tensor是存储和变换数据的主要工具。如果你之前用过NumPy，你会发现Tensor和NumPy的多维数组非常类似。然而，Tensor提供GPU计算和自动求梯度等更多功能，这些使Tensor更加适合深度学习。

"tensor"这个单词一般可译作“张量”，张量可以看作是一个多维数组。标量可以看作是0维张量，向量可以看作1维张量，矩阵可以看作是二维张量。

2.1 创建Tensor

我们先介绍Tensor的最基本功能，即Tensor的创建。

首先导入PyTorch：

import torch

然后我们创建一个5x3的未初始化的Tensor：

torch.empty(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format) → Tensor
返回一个充满未初始化数据的张量。张量的形状由变量参数定义size。

x = torch.empty(5, 3)
print(x)

创建一个5x3的随机初始化的Tensor:

x = torch.rand(5, 3)
print(x)

创建一个5x3的long型全0的Tensor:

x = torch.zeros(5, 3, dtype=torch.long)
print(x)

还可以直接根据数据创建:

x = torch.tensor([5.5, 3])
print(x)

输出

tensor([5.5000, 3.0000])

通过提供包含数值的Python列表(或嵌套列表)来为所需张量中的每个元素赋予确定值

torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])

输出：

tensor([[2, 1, 4, 3],
        [1, 2, 3, 4],
        [4, 3, 2, 1]])

还可以通过现有的Tensor来创建，此方法会默认重用输入Tensor的一些属性，例如数据类型，除非自定义数据类型。

x = x.new_ones(5, 3, dtype=torch.float64)  # 返回的tensor默认具有相同的torch.dtype和torch.device
print(x)

x = torch.randn_like(x, dtype=torch.float) # 指定新的数据类型
print(x) 

我们可以通过shape或者size()来获取Tensor的形状:

print(x.size())
print(x.shape)

注意：返回的torch.Size其实就是一个tuple, 支持所有tuple的操作。

通过numel函数张量中元素的总数

x.numel()

还有很多函数可以创建Tensor，如：

函数	功能
Tensor(*sizes)	基础构造函数
tensor(data,)	类似np.array的构造函数
ones(*sizes)	全1Tensor
zeros(*sizes)	全0Tensor
eye(*sizes)	对角线为1，其他为0
arange(s,e,step)	从s到e，步长为step
linspace(s,e,steps)	从s到e，均匀切分成steps份
rand/randn(*sizes)	均匀/标准分布
normal(mean,std)/uniform(from,to)	正态分布/均匀分布
randperm(m)	随机排列

这些创建方法都可以在创建的时候指定数据类型dtype和存放device(cpu/gpu)。

2.2 操作

算术操作

在PyTorch中，同一种操作可能有很多种形式，下面用加法作为例子。

x = torch.rand(5, 3)
y = torch.rand(5, 3)
print(x + y)
print(torch.add(x, y))

还可指定输出：

result = torch.empty(5, 3)
torch.add(x, y, out=result)
print(result)

还可inplace形式

# adds x to y
y.add_(x)
print(y)

注：PyTorch操作inplace版本都有后缀_, 例如x.copy_(y), x.t_()

常见的标准算术运算符（+、-、*、/和**)都可以被升级为按元素运算

x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x+y,x-y,x*y,x/y,x**y

输出：

(tensor([ 3.,  4.,  6., 10.]),
 tensor([-1.,  0.,  2.,  6.]),
 tensor([ 2.,  4.,  8., 16.]),
 tensor([0.5000, 1.0000, 2.0000, 4.0000]),
 tensor([ 1.,  4., 16., 64.]))

按元素方式应用更多的计算

torch.exp(x)

输出

tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])

我们也可以把多个张量连结在一起，

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3],[1, 2, 3, 4],[4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
# dim=0 在第0维合并，行堆起来
# dim=1 在第1维合并，列堆起来

输出

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [ 2.,  1.,  4.,  3.],
         [ 1.,  2.,  3.,  4.],
         [ 4.,  3.,  2.,  1.]]),
 tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
         [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
         [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))

对张量中的所有元素进行求和会产生一个只有一个元素的张量。

X.sum()

输出：

tensor(66.)

索引

我们还可以使用类似NumPy的索引操作来访问Tensor的一部分，需要注意的是：索引出来的结果与原数据共享内存，也即修改一个，另一个会跟着修改。

y = x[0, :]
y += 1
print(y)
print(x[0, :]) # 源tensor也被改了

除了常用的索引选择数据之外，PyTorch还提供了一些高级的选择函数:

函数	功能
index_select(input, dim, index)	在指定维度dim上选取，比如选取某些行、某些列
masked_select(input, mask)	例子如上，a[a>0]，使用ByteTensor进行选取
nonzero(input)	非0元素的下标
gather(input, dim, index)	根据index，在dim维度上选取数据，输出的size与index一样

改变形状

用view()来改变Tensor的形状:

y = x.view(15)
z = x.view(-1, 5)  # -1所指的维度可以根据其他维度的值推出来
print(x.size(), y.size(), z.size())

注意view()返回的新Tensor与源Tensor虽然可能有不同的size，但是是共享data的，也即更改其中的一个，另外一个也会跟着改变。(顾名思义，view仅仅是改变了对这个张量的观察角度，内部数据并未改变)

所以如果我们想返回一个真正新的副本（即不共享data内存）该怎么办呢？Pytorch还提供了一个reshape()可以改变形状而不改变其值，但是此函数并不能保证返回的是其拷贝，所以不推荐使用要改变一个张量的形状而不改变元素数量和元素值，我们可以调用reshape函数。推荐先用clone创造一个副本然后再使用view。

使用 clone还有一个好处是会被记录在计算图中，即梯度回传到副本时也会传到源 Tensor。

另外一个常用的函数就是item(), 它可以将一个标量Tensor转换成一个Python number：

x = torch.randn(1)
print(x)
print(x.item())

输出

tensor([2.3466])
2.3466382026672363

线性代数

函数	功能
trace	对角线元素之和(矩阵的迹)
diag	对角线元素
triu/tril	矩阵的上三角/下三角，可指定偏移量
mm/bmm	矩阵乘法，batch的矩阵乘法
addmm/addbmm/addmv/addr/baddbmm..	矩阵运算
t	转置
dot/cross	内积/外积
inverse	求逆矩阵
svd	奇异值分解

使用方法

x = torch.rand(4, 4)
print(x)
print(torch.trace(x))
print(torch.diag(x))
print(torch.svd(x))

标量由只有一个元素的张量表示

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y

输出：

(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))

可以将向量视为标量值组成的列表

x = torch.arange(4)
x

输出：

tensor([0, 1, 2, 3])

通过张量的索引来访问任一元素

x[3]

输出：

tensor(3)

访问张量的长度

len(x)

通过指定两个分量m和n来创建一个形状为m*n的矩阵

A = torch.arange(20).reshape(5, 4)
A 

输出：

tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])

矩阵的转置

A.T

对称矩阵（symmetric matrix）A等于其转置A’

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B == B.T

就像向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构

X = torch.arange(24).reshape(2, 3, 4)
X

给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

输出：

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  2.,  4.,  6.],
         [ 8., 10., 12., 14.],
         [16., 18., 20., 22.],
         [24., 26., 28., 30.],
         [32., 34., 36., 38.]]))

具体而言，两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号）。
对于矩阵B， 其中第i行和第j列的元素是bij。 矩阵A和B的Hadamard积为：c_ij = a_ij * b_ij

A * B

输出：

tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])

将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

输出：

(tensor([[[ 2,  3,  4,  5],
          [ 6,  7,  8,  9],
          [10, 11, 12, 13]],
 
         [[14, 15, 16, 17],
          [18, 19, 20, 21],
          [22, 23, 24, 25]]]),
 torch.Size([2, 3, 4]))

计算其元素的和

x = torch.arange(4, dtype=torch.float32)
x, x.sum()

输出：

(tensor([0., 1., 2., 3.]), tensor(6.))

指定张量沿哪一个轴来通过求和

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

输出：

(tensor([40., 45., 50., 55.]), torch.Size([4]))

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

输出

(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

一个与求和相关的量是平均值（mean或average）

A.mean(), A.sum() / A.numel()

输出：

(tensor(9.5000), tensor(9.5000))

同样，计算平均值的函数也可以沿指定轴降低张量的维度。

A.mean(axis=0), A.sum(axis=0) / A.shape[0]

输出：

(tensor([ 8.,  9., 10., 11.]), tensor([ 8.,  9., 10., 11.]))

计算总和或均值时保持轴数不变会很有用

sum_A = A.sum(axis=1, keepdims=True)
sum_A

输出：

tensor([[ 6.],
        [22.],
        [38.],
        [54.],
        [70.]])

通过广播将A除以sum_A

A / sum_A

输出：

tensor([[0.0000, 0.1667, 0.3333, 0.5000],
        [0.1818, 0.2273, 0.2727, 0.3182],
        [0.2105, 0.2368, 0.2632, 0.2895],
        [0.2222, 0.2407, 0.2593, 0.2778],
        [0.2286, 0.2429, 0.2571, 0.2714]])

沿某个轴计算A元素的累积总和，cumsum函数

A.cumsum(axis=0)

输出：

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  6.,  8., 10.],
        [12., 15., 18., 21.],
        [24., 28., 32., 36.],
        [40., 45., 50., 55.]])

点积是相同位置的按元素乘积的和

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

输出：

(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))

我们可以通过执行按元素乘法，然后进行求和来表示两个向量的点积

torch.sum(x * y)

输出：

tensor(6.)

在代码中使用张量表示矩阵-向量积，我们使用与点积相同的mv函数

A.shape, x.shape, torch.mv(A, x)

输出：

(torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

我们可以将矩阵-矩阵乘法AB看作是简单地执m行次矩阵-向量积，并将结果拼接在一起，形成一个n×m矩阵

B = torch.ones(4, 3)
torch.mm(A, B)

输出：

tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

L2范数是向量元素平方和的平方根

u = torch.tensor([3.0, -4.0])
torch.norm(u)

L1范数是向量元素的绝对值之和

torch.abs(u).sum()

矩阵的Frobenius norm是矩阵元素的平方和的平方根

torch.norm(torch.ones((4, 9)))

2.3 广播机制

前面我们看到如何对两个形状相同的Tensor做按元素运算。当对两个形状不同的Tensor按元素运算时，可能会触发广播（broadcasting）机制：先适当复制元素使这两个Tensor形状相同后再按元素运算。例如：

x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)

由于x和y分别是1行2列和3行1列的矩阵，如果要计算x + y，那么x中第一行的2个元素被广播（复制）到了第二行和第三行，而y中第一列的3个元素被广播（复制）到了第二列。如此，就可以对2个3行2列的矩阵按元素相加。

即使形状不同，我们仍然可以通过调用广播机制(broadcasting mechanism)来执行按元素操作

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
print(b)
print(a+b)

2.4 运算的内存开销

前面说了，索引操作是不会开辟新内存的，而像y = x + y这样的运算是会新开内存的，然后将y指向新内存。为了演示这一点，我们可以使用Python自带的id函数：如果两个实例的ID一致，那么它们所对应的内存地址相同；反之则不同。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
y = y + x
print(id(y) == id_before) # False 

如果想指定结果到原来的y的内存，我们可以使用前面介绍的索引来进行替换操作。在下面的例子中，我们把x + y的结果通过[:]写进y对应的内存中。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
y[:] = y + x
print(id(y) == id_before) # True

我们还可以使用运算符全名函数中的out参数或者自加运算符+=(也即add_())达到上述效果，例如torch.add(x, y, out=y)和y += x(y.add_(x))。

x = torch.tensor([1, 2])
y = torch.tensor([3, 4])
id_before = id(y)
torch.add(x, y, out=y) # y += x, y.add_(x)
print(id(y) == id_before) # True

注：虽然 view返回的 Tensor与源 Tensor是共享 data的，但是依然是一个新的 Tensor（因为 Tensor除了包含 data外还有一些其他属性），二者id（内存地址）并不一致。

2.5 Tensor和NumPy相互转换

我们很容易用numpy()和from_numpy()将Tensor和NumPy中的数组相互转换。但是需要注意的一点是： 这两个函数所产生的的Tensor和NumPy中的数组共享相同的内存（所以他们之间的转换很快），改变其中一个时另一个也会改变！！！

还有一个常用的将NumPy中的array转换成Tensor的方法就是torch.tensor(), 需要注意的是，此方法总是会进行数据拷贝（就会消耗更多的时间和空间），所以返回的Tensor和原来的数据不再共享内存。

NumPy数组转Tensor

使用from_numpy()将NumPy数组转换成Tensor:

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
print(a, b)

a += 1
print(a, b)
b += 1
print(a, b)

输出：

[1. 1. 1. 1. 1.] tensor([1., 1., 1., 1., 1.], dtype=torch.float64)
[2. 2. 2. 2. 2.] tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
[3. 3. 3. 3. 3.] tensor([3., 3., 3., 3., 3.], dtype=torch.float64)

所有在CPU上的Tensor（除了CharTensor）都支持与NumPy数组相互转换。

此外上面提到还有一个常用的方法就是直接用torch.tensor()将NumPy数组转换成Tensor，需要注意的是该方法总是会进行数据拷贝，返回的Tensor和原来的数据不再共享内存。

c = torch.tensor(a)
a += 1
print(a, c)

输出

[4. 4. 4. 4. 4.] tensor([3., 3., 3., 3., 3.], dtype=torch.float64)

2.6 Tensor on GPU

用方法to()可以将Tensor在CPU和GPU（需要硬件支持）之间相互移动。

# 以下代码只有在PyTorch GPU版本上才会执行
if torch.cuda.is_available():
    device = torch.device("cuda")          # GPU
    y = torch.ones_like(x, device=device)  # 直接创建一个在GPU上的Tensor
    x = x.to(device)                       # 等价于 .to("cuda")
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # to()还可以同时更改数据类型

三 自动求梯度

在深度学习中，我们经常需要对函数求梯度（gradient）。PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图，并执行反向传播。本节将介绍如何使用autograd包来进行自动求梯度的有关操作。

3.1 概念

上一节介绍的Tensor是这个包的核心类，如果将其属性.requires_grad设置为True，它将开始追踪(track)在其上的所有操作（这样就可以利用链式法则进行梯度传播了）。完成计算后，可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。

注意在y.backward()时，如果y是标量，则不需要为backward()传入任何参数；否则，需要传入一个与y同形的Tensor。解释见3.2节。

如果不想要被继续追踪，可以调用.detach()将其从追踪记录中分离出来，这样就可以防止将来的计算被追踪，这样梯度就传不过去了。此外，还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来，这种方法在评估模型的时候很常用，因为在评估模型时，我们并不需要计算可训练参数（requires_grad=True）的梯度。

Function是另外一个很重要的类。Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图（DAG）。每个Tensor都有一个.grad_fn属性，该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的，若是，则grad_fn返回一个与这些运算相关的对象，否则是None。

下面通过一些例子来理解这些概念。

3.2 Tensor

创建一个Tensor并设置requires_grad=True:

x = torch.ones(2, 2, requires_grad=True)
print(x)
print(x.grad_fn)

输出

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
None

再做一下运算操作：

y = x + 2
print(y)
print(y.grad_fn)

输出

tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward>)
<AddBackward object at 0x1100477b8>

注意x是直接创建的，所以它没有grad_fn, 而y是通过一个加法操作创建的，所以它有一个为的grad_fn。

像x这种直接创建的称为叶子节点，叶子节点对应的grad_fn是None。

print(x.is_leaf, y.is_leaf) # True False

再来点复杂的运算操作：

z = y * y * 3
out = z.mean()
print(z, out)

输出：

tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward>) tensor(27., grad_fn=<MeanBackward1>)

通过.requires_grad_()来用in-place的方式改变requires_grad属性：

a = torch.randn(2, 2) # 缺失情况下默认 requires_grad = False
a = ((a * 3) / (a - 1))
print(a.requires_grad) # False
a.requires_grad_(True)
print(a.requires_grad) # True
b = (a * a).sum()
print(b.grad_fn)

输出：

False
True
<SumBackward0 object at 0x118f50cc0>

3.3 梯度

因为out是一个标量，所以调用backward()时不需要指定求导变量：

out.backward() # 等价于 out.backward(torch.tensor(1.))

我们来看看out关于x的梯度$\frac{d(out)}{dx}$:

print(x.grad)

输出：

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

因为
$$out=\frac{1}{4}\sum _{i=1}^4{z}_i=\frac{1}{4}\sum _{i=1}^{4}3(x_i+2{)}^2$$
所以
$$\frac{\partial o}{\partial x_i}{|}_{x_i=1}=\frac{9}{2}=4.5$$
所以上面的输出是正确的。
数学上，如果有一个函数值和自变量都为向量的函数 $y=f(x)$那么$y$的关于$x$梯度就是一个雅可比矩阵（Jacobian matrix）:

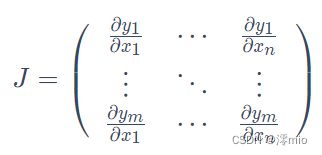
而torch.autograd这个包就是用来计算一些雅克比矩阵的乘积的。例如，如果$v$是一个标量函数$l=g(y)$的梯度

那么根据链式法则我们有$l$关于$x$的雅克比矩阵就为:

注意：grad在反向传播过程中是累加的(accumulated)，这意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需把梯度清零。

# 再来反向传播一次，注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)

out3 = x.sum()
x.grad.data.zero_() # 梯度清零
out3.backward()
print(x.grad)

输出：

tensor([[5.5000, 5.5000],
        [5.5000, 5.5000]])
tensor([[1., 1.],
        [1., 1.]])

为什么在y.backward()时，如果y是标量，则不需要为backward()传入任何参数；否则，需要传入一个与y同形的Tensor? 简单来说就是为了避免向量（甚至更高维张量）对张量求导，而转换成标量对张量求导。举个例子，假设形状为 m x n 的矩阵 X 经过运算得到了 p x q 的矩阵 Y，Y 又经过运算得到了 s x t 的矩阵 Z。那么按照前面讲的规则，dZ/dY 应该是一个 s x t x p x q 四维张量，dY/dX 是一个 p x q x m x n的四维张量。问题来了，怎样反向传播？怎样将两个四维张量相乘？？？这要怎么乘？？？就算能解决两个四维张量怎么乘的问题，四维和三维的张量又怎么乘？导数的导数又怎么求，这一连串的问题，感觉要疯掉…… 为了避免这个问题，我们不允许张量对张量求导，只允许标量对张量求导，求导结果是和自变量同形的张量。所以必要时我们要把张量通过将所有张量的元素加权求和的方式转换为标量，举个例子，假设y由自变量x计算而来，w是和y同形的张量，则y.backward(w)的含义是：先计算l = torch.sum(y * w)，则l是个标量，然后求l对自变量x的导数。 参考

来看一些实际例子。

x = torch.tensor([1.0, 2.0, 3.0, 4.0], requires_grad=True)
y = 2 * x
z = y.view(2, 2)
print(z)

输出：

tensor([[2., 4.],
        [6., 8.]], grad_fn=<ViewBackward>)

现在 z 不是一个标量，所以在调用backward时需要传入一个和z同形的权重向量进行加权求和得到一个标量。

v = torch.tensor([[1.0, 0.1], [0.01, 0.001]], dtype=torch.float)
z.backward(v)
print(x.grad)

输出：

tensor([2.0000, 0.2000, 0.0200, 0.0020])

注意，x.grad是和x同形的张量。

再来看看中断梯度追踪的例子：

x = torch.tensor(1.0, requires_grad=True)
y1 = x ** 2 
with torch.no_grad():
    y2 = x ** 3
y3 = y1 + y2

print(x.requires_grad)
print(y1, y1.requires_grad) # True
print(y2, y2.requires_grad) # False
print(y3, y3.requires_grad) # True

输出：

True
tensor(1., grad_fn=<PowBackward0>) True
tensor(1.) False
tensor(2., grad_fn=<ThAddBackward>) True

可以看到，上面的y2是没有grad_fn而且y2.requires_grad=False的，而y3是有grad_fn的。如果我们将y3对x求梯度的话会是多少呢？

y3.backward()
print(x.grad)

输出：

tensor(2.)

为什么是2呢？$y_3=y_1+y_2=x^2+x^3$，当$x=1$时，$\frac{d{y}_3}{dx}$不应该是5吗？事实上，由于$y_2$的定义是被torch.no_grad()包裹的，所以与$y_2$有关的梯度是不会回传的，只有与$y_1$有关的梯度才会回传，即$x^2$对$x$的梯度

上面提到，y2.requires_grad=False，所以不能调用 y2.backward()，会报错：

RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

此外，如果我们想要修改tensor的数值，但是又不希望被autograd记录（即不会影响反向传播），那么我么可以对tensor.data进行操作。

x = torch.ones(1,requires_grad=True)

print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经是独立于计算图之外

y = 2 * x
x.data *= 100 # 只改变了值，不会记录在计算图，所以不会影响梯度传播

y.backward()
print(x) # 更改data的值也会影响tensor的值
print(x.grad)

输出：

tensor([1.])
False
tensor([100.], requires_grad=True)
tensor([2.])

四 数据预处理

为了能用深度学习来解决现实世界的问题，我们经常从预处理原始数据开始， 而不是从那些准备好的张量格式数据开始。 在Python中常用的数据分析工具中，我们通常使用pandas软件包。 像庞大的Python生态系统中的许多其他扩展包一样，pandas可以与张量兼容。

4.1 读取数据集

举一个例子，我们首先创建一个人工数据集，并存储在CSV（逗号分隔值）文件 …/data/house_tiny.csv中。 以其他格式存储的数据也可以通过类似的方式进行处理。 下面我们将数据集按行写入CSV文件中。

# 创建一个人工数据集，并存储在csv (逗号分隔值)文件
import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

要从创建的CSV文件中加载原始数据集，我们导入pandas包并调用read_csv函数。该数据集有四行三列。其中每行描述了房间数量（“NumRooms”）、巷子类型（“Alley”）和房屋价格（“Price”）。

# 如果没有安装pandas，只需取消对以下行的注释来安装pandas
# !pip install pandas
import pandas as pd

data = pd.read_csv(data_file)
print(data)

输出：

   NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000

4.2 处理缺失值

注意，“NaN”项代表缺失值。 为了处理缺失的数据，典型的方法包括插值法和删除法， 其中插值法用一个替代值弥补缺失值，而删除法则直接忽略缺失值。 在这里，我们将考虑插值法。

通过位置索引iloc，我们将data分成inputs和outputs， 其中前者为data的前两列，而后者为data的最后一列。 对于inputs中缺少的数值，我们用同一列的均值替换“NaN”项。

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
print(inputs)

输出：

   NumRooms Alley
0       3.0  Pave
1       2.0   NaN
2       4.0   NaN
3       3.0   NaN

对于inputs中的类别值或离散值，我们将“NaN”视为一个类别。 由于“巷子类型”（“Alley”）列只接受两种类型的类别值“Pave”和“NaN”， pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。 巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1，“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。

inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

输出：

   NumRooms  Alley_Pave  Alley_nan
0       3.0           1          0
1       2.0           0          1
2       4.0           0          1
3       3.0           0          1

4.3 转换为张量格式

import torch

X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y

输出：

(tensor([[3., 1., 0.],
         [2., 0., 1.],
         [4., 0., 1.],
         [3., 0., 1.]], dtype=torch.float64),
 tensor([127500, 106000, 178100, 140000]))

五 自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。 实际中，根据我们设计的模型，系统会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

5.1 一个简单的例子

作为一个演示例子，假设我们想对函数$y=2x^{T}x$关于列向量$x$求导。 首先，我们创建变量x并为其分配一个初始值。

import torch

x = torch.arange(4.0)
x

输出：

tensor([0., 1., 2., 3.])

在我们计算y关于x的梯度之前，我们需要一个地方来存储梯度。 重要的是，我们不会在每次对一个参数求导时都分配新的内存。 因为我们经常会成千上万次地更新相同的参数，每次都分配新的内存可能很快就会将内存耗尽。 注意，一个标量函数关于向量x的梯度是向量，并且与x具有相同的形状。

x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  # 默认值是None

现在让我们计算y。

y = 2 * torch.dot(x, x)
y

输出：

tensor(28., grad_fn=<MulBackward0>)

x是一个长度为4的向量，计算x和x的点积，得到了我们赋值给y的标量输出。 接下来，我们通过调用反向传播函数来自动计算y关于x每个分量的梯度，并打印这些梯度。

y.backward()
x.grad

输出：

tensor([ 0.,  4.,  8., 12.])

函数$y=2x^{T}x$关于$x$的梯度应为4$x$

x.grad == 4 * x

输出：

tensor([True, True, True, True])

现在让我们计算x的另一个函数。

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad

输出：

tensor([1., 1., 1., 1.])

5.2. 非标量变量的反向传播

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。 对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

然而，虽然这些更奇特的对象确实出现在高级机器学习中（包括深度学习中）， 但当我们调用向量的反向计算时，我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。 这里，我们的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和。

# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 在我们的例子中，我们只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad

输出：

tensor([0., 2., 4., 6.])

5.3. 分离计算

有时，我们希望将某些计算移动到记录的计算图之外。 例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。 想象一下，我们想计算z关于x的梯度，但由于某种原因，我们希望将y视为一个常数， 并且只考虑到x在y被计算后发挥的作用。

在这里，我们可以分离y来返回一个新变量u，该变量与y具有相同的值， 但丢弃计算图中如何计算y的任何信息。 换句话说，梯度不会向后流经u到x。 因此，下面的反向传播函数计算z=ux关于x的偏导数，同时将u作为常数处理， 而不是z=xx*x关于x的偏导数。

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

输出：

tensor([True, True, True, True])

由于记录了y的计算结果，我们可以随后在y上调用反向传播， 得到y=xx关于的x的导数，即2x。

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

输出：

tensor([True, True, True, True])

5.4. Python控制流的梯度计算

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

让我们计算梯度。

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

我们现在可以分析上面定义的f函数。 请注意，它在其输入a中是分段线性的。 换言之，对于任何a，存在某个常量标量k，使得f(a)=k*a，其中k的值取决于输入a。 因此，我们可以用d/a验证梯度是否正确。

a.grad == d / a

输出;

tensor(True)