线性代数 矩阵和向量空间
web.mit.edu/18.06
绘制矩阵:blog.csdn.net/weixin_34130269/article/details/88010192
一.矩阵与方程组
1.方程组的几何解释
(1)行图像(Row picture):1个行图像展示1个方程
2x-y=0 ⇒ x = 1
-x+2y=3 y = 2

(2)列图像(Column picture):方程组对∀b是否有解,等价于列的所有线性组合是否能覆盖整个Rn(在未知数个数=方程数时,n等于二者)
- 如果某些列是其他列的线性组合,并非始终有解,列的所有线性组合只能覆盖Rless_than_n
x [2,-1] + y [-1,2] = [0,3] ⇒ x = 1,y = 2
- Ax就是A的各列的线性组合
[[2 -1],[-1 2]] [x,y] = [0,3]
A x = b
2.高斯-约尔当消元法(Gauss-Jordan Elimination)解方程组:计算机求解方程组的方法
1.选择主元
2.消元--成功/失败-->行阶梯型((Row-echelon Form)
3.回代(Back-Substitution)
4.消元-->行最简型
#成功:
[[1 2 1],[3 8 1],[0 4 1]] ~ [[1 2 1],[0 2 -2],[0 4 1]] ~ [[1 2 1],[0 2 -2],[0 0 5]]
A U
#失败:
#行交换可以解决主元的暂时失效
[[1 2 1],[3 6 1],[0 4 1]] ~ [[1 2 1],[0 0 -2],[0 4 1]] ~ [[1 2 1],[0 4 1],[0 0 -2]]
#永久失效
[[1 2 1],[3 8 1],[0 4 -4]] ~ [[1 2 1],[0 2 -2],[0 4 -4]] ~ [[1 2 1],[0 2 -2],[0 0 0]]
#回代:
[[1 2 1],[0 2 -2],[0 0 5]] = [2,12,2]
U b
#增广(Augmented)矩阵:[A b] (系数矩阵右侧加上结果列向量)
[[1 2 1 2],[3 8 1 12],[0 4 1 2]] ~ [[1 2 1 2],[0 2 -2 6],[0 0 5 -10]]
#即:
x + 2y + z = 2 x = 2
2y - 2z = 6 ⇒ y = 1
5z = -10 z = -2
#转换为行最简型
[[1 2 1],[0 2 -2],[0 0 5]] ~ [[1 0 3],[0 2 -5],[0 0 5]] ~ [[1 0 3],[0 2 0],[0 0 5]] ~ [[1 0 3],[0 1 0],[0 0 1]] ~ [[1 0 0],[0 1 0],[0 0 1]]
3.消元矩阵(E)
[[1 0 0],[-3 1 0],[0 0 1]] * [[1 2 1],[3 8 1],[0 4 1]] = [[1 2 1],[0 2 -2],[0 4 1]]
E21 A
[[1 0 0],[0 1 0],[0 -2 1]] * [[1 2 1],[0 2 -2],[0 4 1]] = [[1 2 1],[0 2 -2],[0 0 5]]
E32 U
[[1 0 0],[0 1 0],[0 -2 1]] * [[1 0 0],[-3 1 0],[0 0 1]] * [[1 2 1],[3 8 1],[0 4 1]] = [[1 2 1],[0 2 -2],[0 0 5]]
E32 E12 A U
E~32 * E~21 * A = U
E * A =U (E = E~32 * E~21)
#如果E21,E32均可逆
#穿脱原则:先进行的变换在逆变换中后进行
#单位矩阵(I/E):对角线上为1,其余均为0
A = E21^(-1) * E32^(-1) * U
A= E^(-1) * U
二.矩阵(Matrix)
1.矩阵的运算
(1)线性运算:
#加/减法:
A~mn ± B~mn = C~mn
c~ij = a~ij ± b~ij
#数乘:用标量(Scalar)乘矩阵
B~mn = k * A~mn
b~mn = k * a~mn
- 线性运算的8条规则:任何满足这8条规则的存在都可被视为向量
u,v,w为向量;a,b为数
1.u + (v + w) = (u + v) + w (加法结合律)
2.v + w = w + v (加法交换律)
3.There is a vector 0 such that 0 + v = v for all v
4.For every v there is a -v so that -v + v = 0
5.a * (b * v) = (a * b) * v (乘法结合律)
6.1 * v = v
7.a * (v + w) = a * v + a * w (乘法分配律)
8.(a + b) * v = a* v + b * v (乘法分配律)
(2)矩阵乘法:用矩阵/向量(Vector)乘矩阵
#常规方法((对应)行 * (对应)列):
[[...]...[c~m1...c~mp]...[...]] * [[...b~1n...]...[...b~pn...]] = [[...]...[...c~mn...]...[...]]
A~kp B~pq C~kq
c~mn= row m of A * column n of B = ∑(c~mi * b~in) (i = 1,2...p)
#列方法:
#C的任何1列都是A中各列的某个线性组合
column i of C = ∑(A * column i of B) (i = 1,2...p)
#行方法:
#C的任何1行都是B中各行的某个线性组合
row i of C = ∑(row i of A * B) (i = 1,2...p)
#(对应)列 * (对应)行:
C = ∑(column i of A * row i of B) (i = 1,2...p)
#分块:
[[A11...A1q]...[Ap1...Apq]] * [[B11...Bt]...[Bq1...Bqt]] = [[C11...C1t]...[Cp1...Cpt]]
A分为p * q块 B分为q * t块 C分为p * t块
Cij = block_row i of A * block_column j of B = ∑(Aip * Bpj) (p = 1,2...q)
A~mn·B~np=C~mp:结果矩阵的行数等于左侧矩阵的行数,列数等于右侧矩阵的列数;左侧矩阵的列数需等于右侧矩阵的行数才可乘
A~1n·B~np=C~1p:行向量*矩阵=行向量;矩阵各行的线性组合
A~mn·B~n1=C~m1:列向量*矩阵=列向量;矩阵各列的线性组合
(3)逆(Inverse)矩阵/非奇异(Non-singular)矩阵(相当于除法;A^(-1)):
- 要求A是方阵
#如果A可逆:
A~n^(-1) * A~n = A~n * A~n^(-1) = I~n
左可逆 右可逆
[[1 0 0],[0 1 0],[0 0 1]] = [[1 0 0],[3 1 0],[0 0 1]] * [[1 0 0],[-3 1 0],[0 0 1]] = [[1 0 0],[-3 1 0],[0 0 1]] * [[1 0 0],[3 1 0],[0 0 1]]
I A^(-1) A
#如A,B均可逆:
(A * B)^(-1) = B^(-1) * A^(-1)
A * B * (B^(-1) * A^(-1)) = A * B * B^(-1) * A^(-1) = A * A^(-1) = I
(A^T)^(-1) = (A^(-1))^T
A^T * (A^(-1))^T = (A^(-1) * A)^T = I^T =I
#利用高斯-约尔当消元法求A^(-1):
[A E] ~ [E A^(-1)]
A^(-1) * [A E] = [A^(-1) * A A^(-1) * E] = [E A^(-1)]
- A可逆的等价说法:
·A(左/右)可逆
·A非奇异(Non-Singular)
·det A ≠ 0
·A中各行/列线性无关
·Ax = 0的解只有零向量
假设A可逆,且Ax=0的解包括非零向量
Ax = 0
A^(-1)Ax = 0
x = 0
与假设矛盾
·A行等价于I
·det A ≠ 0
·A满秩
·A^(-1)或A^T或A^k或A*可逆
·A~n的行/列阶梯型有n个非0行/列
·A的行/列最简型为I
·A的标准型为I
·A可表示为有限个初等矩阵的积
2.矩阵的LU分解
- 上三角(Upper Triangular)矩阵(U):只有对角线上即其上方有非0元素
- 下三角(Lower Triangular)矩阵(L):只有对角线上即其下方有非0元素
- 对角(Diagonal)矩阵(D):对角线上为非0元素,取余均为0
#如果A在消元时不需要互换行
E * A = U ⇒ A = L * U = L * D * U'
[[1 0],[-4 1]] * [[2 1],[8 7]] = [[2 1],[0 3]] ⇒ [[2 1],[8 7]] = [[1 0],[4 1]] * [[2 1],[0 3]] = [[1 0],[4 1]] * [[2 0],[0 3]] * [[1 1/2],[0 1]]
E21 A U L D L'
#如果A在消元时需要互换行
P * A = L * U
#如果消元过程中没有换行,消元乘数(即E中元素)可以直接取绝对值,然后写到L相应位置
E = [[1 0],[-4 1]],L = [[1 0],[4 1]]
#消元次数(步骤数Cost):
#记1次乘+1次加为1个步骤(对1行的1次消元使步骤数+n(等于列数))
#对A~n ⇒ U~n
C = ∑(i * (i - 1)) (i = 2...n) ≈ Σ(i^2) ≈ ∫(0,n)(i^2)di = (n^3)/3 ∝ n^3
#对b~n1 ⇒ b'~n1 (跟随A进行消元)
C = Σ(i) (i = 1...n-1) = n * (n - 1) / 2 ≈ (n^2) / 2 ∝ n^2
3.转置(Transposed)矩阵(A^T):
a~ij = (a^T)~ji
A* A^T在A的各行线性无关时可逆,此时(A * A^T)^T = A * A^T
A^T * A * x = 0 ⇒ x^T * A^T *A * x = 0 ⇒
(A * x)^T * (A * x) = 0 ⇒
A * x = 0 =A各列线性无关 =>
x = 0 =矩阵可逆,零空间为{0} =>
A^T * A可逆
N(A^T * A) = N(A)
rank A^T * A = rank A
4.特殊矩阵
(1)方阵(Square Matrix):
#行数 = 列数,记为A~n,可称为n阶方阵
(2)对称(Symmetric)矩阵:
- 要求为方阵
- 该概念适用于实矩阵,对于复矩阵,有类似的概念"埃尔米特矩阵"
S^T = S OR s~ij = s~ji
#任何矩阵乘其转置都得到对称矩阵:
R^T * R = S
(R^T * R)^T = R^T * R^(TT) = R^T * R
#反对称(Anti-Symmetric)矩阵:AS^T = -AS OR as~ij = - as~ji
#主对角线上的元素全部为0
- 单位(Identity)矩阵(I/E):
I~ii = 1 AND I~mn = 0
#对角线上元素均为1,其余元素均为0
(3)零矩阵(O):
o~ij = 0
#所有元素均为0
(4)置换(Permutation)矩阵( P):
#P~n是行经过重新排列的I~n
#对n阶而言,有n!个
#Pi * Pj ∈ Set P;Pi^(-1) = P^T ∈ Set P
#(P~n构成1个对矩阵乘法和逆封闭的群)
#以3阶为例:
[[1 0 0],[0 1 0],[0 0 1]],[[0 1 0],[1 0 0],[0 0 1]],[[0 0 1],[0 1 0],[1 0 0]],
[[1 0 0],[0 0 1],[0 1 0]],[[0 1 0],[0 0 1],[1 0 0]],[[0 0 1],[1 0 0],[0 1 0]]
#行置换矩阵:
#乘在原矩阵左侧
[[0 1],[1 0]] * [[a b],[c d]] = [[c d],[a b]]
#列置换矩阵
#乘在原矩阵右侧
[[a b],[c d]] * [[0 1],[1 0]] = [[b a],[d c]]
(5)r = 1的矩阵:
r = 1的矩阵可以写成列向量与行向量之积
A = [[1 4 5],[2 8 10]] = [1 2]^T * [1 4 5]
1个r = x的矩阵可以被分解为x个r = 1的矩阵
r = 1的矩阵可以视为基
max{rank A,rank B} ≤ rank (A + B) ≤ rank A + rank B
(6)旋转(Rotation)矩阵(Q):
乘以一个向量时改变向量的方向但不改变大小并保持手性不变的矩阵
#实例:
Q = [0 -1,1 0]#使向量逆时针旋转90°
7.正矩阵(Positive Matrix):
对矩阵A,若∀a~ij>0,则称A为正矩阵,记为A>0
5.矩阵的迹(Trace):
即矩阵所有特征值的和,记为tr(A)
#即Tr(A) = Σ(λi) (i = 1...n),记为tr(A)
#性质:
矩阵的迹等于矩阵对角线上所有元素的和,即Tr(A) = Σ(a~ii) (i = 1...n)
三.向量空间(Vector Space)
1.向量空间
(1)R^n:所有n维实向量(Real Vector)构成的空间
R^1:1条过原点的直线
R^2:1个过原点的平面
R^3:1个过原点的3维空间
(2)向量空间对加法和数乘是封闭的(closed)(向量空间中任意2个向量的线性组合仍在该向量空间中)
- 必定包含0向量(vec a - vec a = 0)
2.子空间(Sub-space):1个嵌在向量空间中(是另1个向量空间的一部分)的向量空间
- A * x = b在b ≠ 零向量时的解均不构成子空间:
解中不包含0向量
解的集合是R^n平移到不过原点的位置
(1)Rm(m ≤ n)是Rn的子空间
R^2的子空间:
整个R^2
L:任何过(0,0)的直线(R^1)
Z:0向量(R^0)
(2)4个重要子空间:
1.列空间(Column Space;C(A)):矩阵各列的所有线性组合
C(A) in R^m;dim C(A) = r
#Ax = b不总是有解(C(A)无法填充整个R^m):仅当b ∈ C(A)时有解
#Ax = 0总是有解(0向量永远在C(A)中)
#1组基是所有主列
#实例:
A~32 = [[1 3],[2 3],[4 1]]
C(A):(10/3)x - (11/3)y + z = 0 OR x * [1 2 4]^T + y * [3 3 1]^T
a R^2 in R^3
A~43 = [[1 1 2],[2 1 3],[3 1 4],[4 1 5]]#第3列与前2列线性相关
C(A) = x * [1 2 3 4]^T + y * [1 1 1 1]^T
a R^2 in R^4
2.行空间(Row Space;C(A^T)):矩阵各行的所有线性组合,即转置矩阵的列空间
C(A^T) in R^n;dim C(A^T) = r
#1组基是R的前r行
#行变换不改变行空间
3.零空间(Null Space;N(A)):Ax = 0的解构成的空间
N(A) in R^n;dim N(A) = n - r
#性质:设A为矩阵,v,w为向量,k为常数
A * v = 0 AND A * w = 0 ⇒ A * (v + w) = 0 ⇒ v + w ∈ N(A)
A * (k * v) = 0 ⇒ k * A * v = 0
#1组基是所有自由列
#实例:
A~43 = [[1 1 2],[2 1 3],[3 1 4],[4 1 5]]
N(A) = [c,c,-c] (c为∀常数)
a R^1 in R^3
#求解零空间过程见 四.1
4.左零空间(Left-Null Space;N(A^T)):转置矩阵的零空间
N(A^T) in R^m;dim N(A^T) = m - r
#为何称为左零空间(非正式):
A^T * y = 0~n1 ⇒ (A^T * y)^T = 0^T ⇒ y^T * A = 0~1n
#N(A^T)的1组基是E(E = R * A^(-1))的后m - r行
E * [A~mn I~m] = [R~mn E~m]
R的后m - r行为零向量,即E的后m - r行乘A得到零向量
#维度:
dim C(A^T) + dim N(A) = n
dim C(A) + dim N(A^T) = m
#嵌入:
C(A),N(A^T) in R^m
C(A^T),N(A) in R^n
#基本变换与行/列空间:
行变换不改变行空间,但会改变列空间;列变换相反
#正交:
C(A)与N(A^T)是R^n中的正交补(Orthogonal Complements)
#即C(A)包括且只包括R^n中所有与N(A^T)正交的向量
证明同理
C(A^T)与N(A)是R^n中的正交补
1.A * x = 0 ⇒ [row 1,row 2...row n] * x = 0 ⇒ [row i] * x = 0 (i = 1...n) ⇒ x与C(A^T)的1组基正交 ⇒ C(A^T) ⊥ N(A)
2.dim C(A^T) + dim N(A) = n
(4)性质:
Sub-space1 ∪ Sub-space2 is not Sub-space (除非1是2的子集)
Sub-space1 ∩ Sub-space2 is Sub-space2
(5)零和向量空间
向量空间中所有向量维度相同,每个向量的各分量和为0
S = [[xi1 xi2 ... xin]^T ...] (xi1 + xi2... + xin = 0) (i = 1,2...m)
(xi1 + ... + xin) + (xj1 + ... + xjn) = 0
k * (xi1 + ... + xin) = 0
dim S = n - 1
S = N([1 1 ... 1])
[1 ... 1] * [[x11 x12 ... x1n]^T ... [xi1 ... xin]] = [x11 + x12 + ... + x1n ... xi1 + xi2 + ... + xin] = 0
3.秩(Rank;r):
矩阵主元(Pivot)的个数
消元得到行阶梯型矩阵(R)后,主元所在的列为主列(Pivot Column),其余列为自由列(Free Column)
自由变量的个数即为n - r
对A~mn,r ≤ min{m,n}
4.基(Basis):
向量空间的一组基:一组向量,这些向量线性无关且能生成这个向量空间
#不多(线性无关)不少(可以生成这个向量空间)
#对R^n,其∀1组基构成的的矩阵需要可逆
#∀1个向量空间都有无穷多组基
#1个给定向量空间的每组基向量的个数都相等
#列空间的1组基是其所有主列
5.维数(Dimension):
向量空间S的1组基中向量的个数,记作dim S
#dim C(A) = r (主向量的个数)
#dim N(A) = n - r (自由向量的个数)
*6.一些特别的向量空间
(1)矩阵构成的向量空间
#将矩阵看作向量
#矩阵加法/数乘的运算律与向量相同
#所有矩阵构成的向量空间的一些子空间:
#所有m * n的矩阵M:dim M = m * n (R^n ⇒ R^(m * n) )
#n阶方阵 = S + U:dim (S + U) = n^2
#所有上/下三角矩阵U/L:dim U~n = (n^2 + n) / 2
#所有对称矩阵S:dim S~n = dim U~n
#对角矩阵D = U ∩ S:dim D~n = n
#3阶方阵向量空间M的子空间
#3阶U/L:dim U = 3 * 3 = 9
[[1 0 0],[0 0 0 ],[0 0 0]]...[[0 0 0],[0 0 0],[0 0 1]]
#3阶S:dim S = 6
[[1 0 0],[0 0 0],[0 0 0]]...[[0 0 0],[0 0 0],[0 0 1]],[[0 1 0],[1 0 0],[0 0 0]]...[[0 0 0],[0 0 1],[0 1 0]]
#3阶U/L ∩ 3阶S = 3阶D:dim D = 3
[[1 0 0],[0 0 0],[0 0 0]]...[[0 0 0],[0 0 0],[0 0 1]]
#M = S + U:dim(S + U) = 9
#dim (S ∩ U) + dim (S + U) = dim S + dim U
(2)线性微分方程的通解:
#示例:
y''(x) + y(x) = 0
1组基:sin(x),cos(x)
向量空间:y = C1 * sin(x) + C2 * cos(x)
dim (Solution Space) = 2
四.方程组可解性(Solvability)及求解方法
- 当b ∈ C(A),有解
- 特别地,当b为0向量,始终有解
1.A * x = 0 (齐次方程组)
[[1 2 2 2],[2 4 6 8],[3 6 8 10]]
#解出零空间(A * x = 0 ⇒ U * x = 0 ⇒ R * x = 0)
#消元得到行阶梯型(消元不改变零空间)
A = [[1 2 2 2],[2 4 6 8],[3 6 8 10]] ⇒ [[1 2 2 2],[0 0 2 4],[0 0 2 4]] ⇒ [[1 2 2 2],[0 0 2 4],[0 0 0 0]] = U1
#找出n - r个线性无关的特解(数量等于自由变量数)
#通常在1个特解中,1个自由变量取1,其余自由变量取0(即用自由变量表示主变量)
r1 = [-2 1 0 0]^T,r2 = [2 0 -2 1]
#这r个特解的线性组合为零空间
N(A) = x2 * r1 + x4 * r2 = x2 * [-2 1 0 0]^T + x4 * [2 0 -2 1]^T
#消元得到行最简型
[[1 2 2 2],[0 0 2 4],[0 0 0 0]] ⇒ [[1 2 0 -2],[0 0 1 2],[0 0 0 0]]
#回代相当于利用列变换将矩阵变成标准型(Reduced Row-echelon Form;R)
#R的形式为[[I~rr F~r(n-r)],[O~(n-r)r O~(n-r)(n-r)]]
#F是自由变量构成的矩阵
[[1 2 0 -2],[0 0 1 2],[0 0 0 0]] ⇒ [[1 0 2 -2],[0 1 0 2],[0 0 0 0]]
R
#利用零空间矩阵(Nullspace Matrix)1次找出所有解R * N = O
#N为所有解构成的矩阵,即N = [x1 x2...xn]
R * N = O ⇒ N = [-F,I] ⇒ R * x = 0 ⇒ [[I F],[O O]] * [x~pivot,x~free] = O ⇒ x~pivot = - F * x~free
[[1 0 2 -2],[0 1 0 2],[0 0 0 0]] ⇒ N = [[2 -2,0 -2],[1 0,0 1]] ⇒ x
#(注意此时变量顺序已发生改变)
#当N(A) = R^0.只有零解;当N(A) ≠ R^0,有非零解
当m < n:一定有非零解
2.A * x = b (非齐次方程组)
- 如果A各行的线性组合(系数不均为0)可以得到0向量,b各行的相同线性组合也需要为0
- 解的几何表示:N(A)平移到过x~p的位置
#当方程有解:
#将所有自由变量设为0
x2 = 0,x4 = 0
#在自由变量均为0的情况下解出A * x = b的1个特解x~p
x1 + 2x3 = 1 ⇒ x1 = - 2
2x3 = 3 x3 = 3 / 2
x~p = [-2 0 3/2 0]^T
#求出A的零空间
N(A) = x2 * [-2 1 0 0]^T + x4 * [2 0 -2 1]^T
#将N(A)与x~p相加得到所有解
A * x~p = b
A * x~n = 0
A * (x~p + x~n) = A * x~p + A * x~n = b + 0 = b
x = N(A) + b = x2 * [-2 1 0 0]^T + x4 * [2 0 -2 1]^T + [-2 0 3/2 0]^T
A~mn,rank A = r
#如果列满秩(Full Column Rank):r = n < m
N(A) = {0} AND R = [I,O]
x = x~p(唯一解;Unique Solution)或无解(0解/1解)
#如果行满秩(Full Row Rank):r = m < n
有n - m = n -r个自由变量 AND R = [I F] (实际上主变量与自由变量交插出现)
x = x~p或c * x1 + d * x2 + x~p(1/∞解)
#如果满秩(Full Rank):r = m =n
N(A) = {0} AND R = I
x = x~p(1解)
#如果不满秩:r < min{m,n}
R = [[I F],[O O]]
x = c * x1 + d * x2 + x~p或无解(0/∞解)
3.解的结构
(1)A * x = 0:
x = c * x1 + d * x2
#x1,x2为方程的两个特解;c,d为∀实数
(2)A * x = b:
x = N(A) + x~p = c * x1 + d * x2 + x~p
#x~p为A * x = b的1个特解
五.线性相关性(Linear Independence)
1.定义:
对向量x1...xn,如果不存在c1...cn(c1^2 + ... + cn^2≠0)使c1 * x1 + ... + cn * xn = 0,则称x1...xn线性无关;反之称为线性相关
#如果1组向量中包含零向量,这组向量一定线性相关
c1 * 0 + 0 * x2 + ... + 0 * xn = 0
#如果向量数超过其维数,这组向量一定线性相关
A * x = 0在m < n时一定有非零解
2.矩阵的列的线性无关性:
#与A * x =0的解
A * x = 0如果无非零解(A的零空间只包括零向量),A的各列线性无关
A * x = 0只存在零解 ⇒ [α1 α2...αn] * [x1 x2...xn]^T = 0只存在零解 ⇒ α1 * x1 + α2 * x2 + ... + αn * xn = 0只存在零解
#与零空间
#当r = n时A的各列线性无关(无自由变量)
#当r < n时A的各列线性相关
#互相垂直的各列一定线性无关
3.向量组生成(Span)向量空间:
这个向量空间由这个向量组所有向量的全部线性组合组成
#矩阵的列生成列空间
六.正交(Orthogonality)和投影
1.正交(Orthogonal)向量/子空间:
#正交向量:
x与y正交 <==> x ⊥ y <==> x · y^T = 0 <==> |x|^2 + |y|^2 = |x + y|^2
向量x的长度 = x · x^T
|x|^2 + |y|^2 = |x + y|^2 ⇒ x · x^T + y · y^T = (x + y) · (x + y)^T ⇒ 0 = x · y^T + y · x^T ⇒ x · y^T = 0
零向量与任何向量正交
#正交子空间
子空间S与子空间T正交 <==> S中的∀向量与T中的∀向量正交
如果S和T在非0向量处相交,S一定不和T正交
C(A) ⊥ N(A^T),C(A^T) ⊥ N(A)
#对2维向量
#a,b为行向量,将b投影到a上
#p,a,b关系:
p ⊥ e ⇒ a * (b - x * a)^T = 0 ⇒
x * a * a^T = a * b ⇒
x = (a * b) / (a * a^T) ⇒
p = x * a^T ⇒
p = [(a * b) / (a * a^T)] * a^T
#投影矩阵P:
p = P * b ⇒
P = (a^T * a) / (a * a^T)
#性质:
C(P) = 1条过a,平行于向量a的直线
rank P = 1
P^T = P
P^T = ((a^T * a) / (a * a^T) )^T = (a^T * a)^T / (a * a^T) = P
P^2 = P
#对n维向量空间
#b,a1,a2...an为列向量,A以a1,a2...an为基,将b投影到C(A)上
p = A * x' (为列向量)
e = b - p ⊥ C(A) ⇒
e ⊥ a1 ... an ⇒
e ⊥ C(A)
[a1^T...]^T * (b - A * x') = [0 ... 0]^T即A^T * (b - A * x') = 0 ⇒
A^T * A * x' = A^T * b ⇒
x' = A^T * (A^T * A)^(-1) * b ⇒
p = A * (A^T * A)^(-1) * A^T * b ⇒
P = A * (A^T * A)^(-1) * A^T
#如果A是方阵:P = I,C(A) = R^n,b在C(A)中,P * b = b
#如果b ⊥ C(A):b in N(A^T),P * b = 0
#性质:P^T = P,P^2 = P
投影到与C(A)垂直的空间上,投影矩阵为P' = I - P,P'性质同P
p + e = b
e = (I - P) * b
(2)应用:在A~mn * x = b (m > n)无解时"求解"该方程
即解出最接近的解
利用(A^T)~nm * A~mn = S~n,S一定可逆
求解A^T * A * x' = A^T * b#一定可解
3.最小二乘法(Least Squares):线性回归分析(Linear Regression)
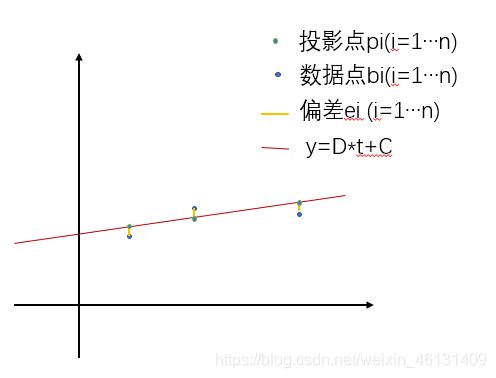
数据点b1(t1,y1),b2(t2,y2)...bn(tn,yn);拟合曲线y = D * t + C
求曲线,要求:D * ti + C = yi (i = 1 ... n)
即:[[1 t1],[1 t2]...[1 ti]] * [C D]^T = [y1 y2 ... yn]^T (无解)
最优解使|A * x - b|^2 = e^2 = e1^2 + ... + en^2最小
即:Σ(D * ti - C - yi)^2 (i = 1 ... n)最小
求解x' = [C' D']^T和p
A^T * A * x' = A^T * b,p = A * x'
实例:
数据点(1,1),(2,2),(3,2) ⇒ 方程组:C + D = 1,C + 2D =2,C + 3D =2
[[1 1 1],[1 2 3]] * [[1 1 1],[1 2 3],[1 2 2]]^T = [[3 6 5],[6 14 11]]
A^T [A b]
新方程组:3C + 6D = 5,6C + 14D = 11(正规方程组;Normal Equations)
最优直线:y = t / 2 + 2 / 3
易受离群值(Outlier)影响:如果有远离大多数点的点,偏差将极大
4.标准正交向量组(Orthonormal Vectors):
(1)概念:
q1,q2...qn均为列向量
由互相垂直的单位向量构成的向量组
qi^T * qj = 0 (i ≠ j) OR 1 (i = j) (即|qi| = 1 (i = 1 ... n) AND qi ⊥ qj)
#实例:[1 0 0]&[0 1 0]&[0 0 1],[cosθ,sinθ]&[-sinθ,cosθ]
标准正交向量:a ⊥ b且|a| = |b| = 1
标准正交基(Orthonormal Basis):标准正交向量组作为基
(2)正交矩阵(Orthogonal Matrix;Q):
#有标准正交列的矩阵(Matrix with Orthonormal Columns):
Q = [q1 q2 ... qn]
Q^T * Q = [q1^T,q2^T,...qn^T] * [q1 q2...qn] = I
投影矩阵P = Q * (Q^T * Q)^(-1) * Q^T = Q * Q^T
#实例:Q = [1 -2,2 -1,2 2] / 3
#当Q为方阵,称为正交矩阵(Orthogonal Matrix)
#习惯上不称为标准正交矩阵(Orthonormal Matrix)
此时Q可逆,Q^(-1) = Q^T
投影矩阵P = Q * Q^T = I
#实例:
置换矩阵,Q = [cosθ -sinθ,sinθ cosθ],Q = [1 1,1 -1] / (2)^(1/2)
#正规方程:
Q^T * Q * x' = Q^T * b ⇒ x' = Q^T * b ⇒ x'i = qi^T * b
#阿德玛矩阵(Adhemar Matrix):仅由1,-1构成的正交矩阵
#已知在n = 2,4,16,64...时存在,在哪些维度下成立的规律未知
#实例:
Q = [1 1 1 1,1 -1 1 -1,1 1 -1 -1,1 -1 -1 1] / 2
(3)格拉姆-施密特正交化(Graham-Schmidt Calculation):由线性无关向量构造标准正交向量

#步骤:
线性无关向量a1,a2 ... an ⇒
正交向量组a1',a2' ... an' ⇒
标准正交向量组q1 = a1' / |a1'|,q2 = a2' / |a2'| ... qn = an' / |an'|
#缺点:经常出现根号
#当n = 2:
a,b为线性无关的列向量
a' = a
b' = b - p = b - [(a'^T * b) / (a'^T * a')] * a'
q1 = a' / |a'|
q2 = b' / |b'|
#当n = 3:
a,b,c为线性无关的列向量
a' = a
b' = b - [(a'^T * b) / (a'^T * a')] * a'
c' = c - [(a'^T * c) / (a'^T * a')] * a' - [(b'^T * c) / (b'^T * b')] * b'
减去a方向上的分量 减去b方向上的分量
q1 = a' / |a'|
q2 = b' / |b'|
q3 = c' / |c'|
#当n ≥ 4:同理
#实例:
a = [1,1,1],b = [1,0,2],c = []
a' = a = [1,1,1]
b' = b - [(a^T * b) / (a^T * a)] * a = [1,0,2] - (3 / 3) * [1,1,1] = [0,-1,1]
Q = [q1 q2] = [a' / |a'| b' / |b'|] = [[1 / 3,1 / 3,1 / 3] [0,-1 / sqrt(2),1 / sqrt(2)]]
#总结:
ai' = ai - Σ{[(aj^T * ai) / (aj^T * aj)] * aj} (i = 1,2...n;j < i)
qi = ai' / |ai'|
(4)矩阵的QR分解
A = Q * R
#A的列向量线性无关;Q的列向量是由A的列向量构造的标准正交向量组
#故C(A) = C(Q)
#a1,a2...q1,q2...均为列向量
A = [a1 a2],Q = [q1 q2] ⇒
R = [a1^T * q1,a2^T * q1;a1^T * q2,a2^T * q2] = [a1^T * q1,a2^T * q1;0,a2^T * q2]
#由于qi ⊥ qj (j < i),故R为上三角矩阵
#矩阵Q的性质:Q^(-1) = Q^T ⇐ Q * Q^T = E
BTW.线性代数与图论(Graphs)
(1)图(Graphs):边(Edge)和节点(Node)的集合,边连接节点
(2)1个包含n个节点,m条边的图可以用1个m * n的矩阵表示
(3)研究人际关系(人为节点,关系为边),互联网
距离:从1个节点到另1个节点最少需要经过多少条边
六度分离理论(Six Degrees of Separation)—小世界图
(4)电路分析: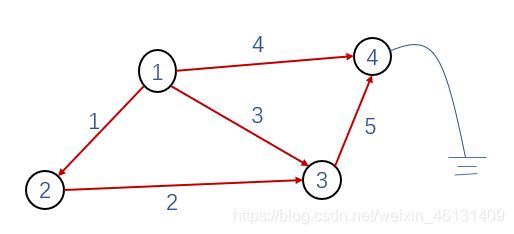
关联矩阵(Incidence Matrix):
A = [[-1 1 0 0],[0 -1 1 0],[-1 0 1 0],[-1 0 0 1],[0 0 -1 1]]#-1指电流从此流出,1指电流流入这里
dim C(A) = dim C(A^T) = 3
非0元素共2m个
回路(Loop):起点和终点相同的路径,如边1,2,3构成1个回路
1个回路的边所在的各行线性相关
树(Tree):无回路的图,如边1,2,4
如果存在n个节点,树中最多有n - 1条边,故r = n - 1
A * x = [x2 - x1 x3 - x2 x3 - x1 x4 - x1 x4 - x3]^T
xi (i = 1 ... 4)代表对应结点的电势(Potential) = A * x = e (电势) =>
xi - xj代表对应边上的电势差(Potential Difference) = y = ρ * e (电导率;欧姆定律) =>
N(A) = C * [1 1 1 1]^T#所有结点的电势由1个常数决定,进而决定电势差然后是电流
Node4接地,电势为0 ==> 求出其他结点电势
任意3个结点电势线性无关,第4个接地
dim N(A) = 1,r A = 3 (相互无关的边数),dim N(A^T) = 2 (相互无关的回路数量)
A^T * y = [- y1 - y3 - y4 y1 - y2 y2 + y3 - y5 y4 + y5]
yi (i = 1 ... 5)代表对应边上的电流(Current) = A^T * y = f (外部输入电流) =>
A^T * y = 0(基尔霍夫电流定律KCL)
(任何结点的电流在电荷不积累,无电源时流入=流出)
N(A^T) = a * [1 1 -1 0] + b * [0 0 1 -1 1]
基本方程:A^T * ρ * A * x = f
dim N(A^T) = m - r = m - (n - 1)
loops = edges - nodes + 1
nodes - edges + loops = 1 (欧拉公式)


