分类交叉熵Cross-Entropy
一、简介
在二分类问题中,你可以根据神经网络节点的输出,通过一个激活函数如Sigmoid,将其转换为属于某一类的概率,为了给出具体的分类结果,你可以取0.5作为阈值,凡是大于0.5的样本被认为是正类,小于0.5则认为是负类
然而这样的做法并不容易推广到多分类问题。多分类问题神经网络最常用的方法是根据类别个数n,设置n个输出节点,这样每个样本神经网络都会给出一个n维数组作为输出结果,然后我们运用激活函数如softmax,将输出转换为一种概率分布,其中的每一个概率代表了该样本属于某类的概率。
比如一个手写数字识别这种简单的10分类问题,对于数字1的识别,神经网络模型的输出结果应该越接近[0,1,0,0,0,0,0,0,0,0]
越好,其中[0,1,0,0,0,0,0,0,0,0]
是最理想的结果了
但是如何衡量一个神经网络输出向量和理想的向量的接近程度呢?交叉熵(cross entropy)就是这个评价方法之一,他刻画了两个概率分布之间的距离,是多分类问题中常用的一种损失函数
二、交叉熵
给定两个概率分布:p(理想结果即正确标签向量)和q(神经网络输出结果即经过softmax转换后的结果向量),则通过q来表示p的交叉熵为:
H(p,q)=−∑xp(x)logq(x)
注意:既然p和q都是一种概率分布,那么对于任意的x,应该属于[0,1]
并且所有概率和为1
∀xp(X=x)ϵ[0,1]
且∑xp(X=x)=1
交叉熵刻画的是通过概率分布q来表达概率分布p的困难程度,其中p是正确答案,q是预测值,也就是交叉熵值越小,两个概率分布越接近
三、三分类实例讲解交叉熵
其中某个样本的正确答案即p是[1,0,0]
,某模型经过Softmax激活后的答案即预测值q是[0.5,0.4,0.1]
,那么这个预测值和正确答案之间的交叉熵为:
H(p=[1,0,0],q=[0.5,0.4,0.1])=−(1∗log0.5+0∗log0.4+0∗log0.1)≈0.3
如果另外一个模型的预测值q是[0.8,0.1,0.1]
,那么这个预测值和正确答案之间的交叉熵为:
H(p=[1,0,0],q=[0.8,0.1,0.1])=−(1∗log0.8+0∗log0.1+0∗log0.1)≈0.1
从直观上可以很容易的知道第二个预测答案要优于第一个,通过交叉熵计算得到的结果也是一致的(第二个交叉熵值更小)
而TF中很容易做到交叉熵的计算:
| 1 2 3 |
|
上述代码包含了四种不同的TF运算,解释如下:
1)tf.clip_by_value():将一个张量中的数值限制在一个范围内,如限制在[0.1,1.0]
范围内,可以避免一些运算错误,如预测结果q中元素可能为0,这样的话log0是无效的
| 1 2 3 4 |
|
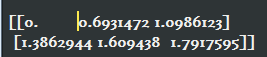
2)tf.log():对张量中的所有元素依次求对数
| 1 2 3 4 |
|
3)乘法运算:*操作,是元素之间直接相乘,而矩阵相乘用tf.matmul函数来完成
| 1 2 3 4 5 6 |
|
4)求和:上面三个运算完成了每个样例中每个类别的交叉熵p(x)logq(x)
的计算,还未进行求和运算
即:三步计算后得到的结果是个n * m的二维矩阵,其中n为一个batch中样本数量,m为分类的类别数量,比如十分类问题,m为10.根据交叉熵公式
最后是要将每行中m个结果相加得到每个样本的交叉熵,然后再对这n行取平均得到一个batch的平均交叉熵,即-tf.reduce_mean()函数来实现
总结:因为交叉熵一般会与softmax一起使用,所以TF对这两个功能进行了封装,并提供了tf.nn.softmax_cross_entropy_with_logits函数
| 1 2 3 4 |
|
关于Softmax计算过程,可以参考:实战Google深度学习框架-C4-深层神经网络