深度学习概念随笔

step，epoch，batchsize，iteration的区别和联系

随机种子概念（已tf为例）

一.基本理解
1.随机函数random遵循随机序列去生成随机数，随机序列由全局随机种子和操作种子共通决定，如果都不设置，哪每次生成随机数的时候，随机序列都由系统自选，这会导致同一个代码多次运行的随机数不一致如下图

a = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(a)
b = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(b)
c = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(c)
d = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(d)
e = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(e)

执行两次的结果不一致


2.当设置了全局种子或操作种子中的一个或两个都设置后，随机序列也就定了，无论执行几次生成的随机数据都是一样的。

tf.random.set_seed(5)
a = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(a)
b = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(b)
c = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(c)
d = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(d)
e = tf.random.uniform(shape=[], maxval=8, dtype=tf.int32)
print(e)

两次执行结果一致

2.特例
当随机操作在函数中时，函数外多次重启调用，生成的随机数据是不一样的。如果要想使之一样可以使用如下函数定义随机数

tf.random.stateless_uniform(
    shape, seed, minval=0, maxval=None, dtype=tf.dtypes.float32, name=None,
    alg='auto_select'
)

tf张量的定义和np数据的转换

tf张量的定义

张量有三种，常量，变量，占位符（不需要初始化的变量）
常张量

tf.constant(
    value, dtype=None, shape=None, name='Const'
)

变张量

tf.Variable(
    initial_value=None, trainable=None, validate_shape=True, caching_device=None,
    name=None, variable_def=None, dtype=None, import_scope=None, constraint=None,
    synchronization=tf.VariableSynchronization.AUTO,
    aggregation=tf.compat.v1.VariableAggregation.NONE, shape=None
)

name_varible = tf.Variable(initial_value=(5,20),shape=(2,))
print(name_varible)
name_varible.assign([10,60])
print(name_varible)

执行结果

<tf.Variable 'Variable:0' shape=(2,) dtype=int32, numpy=array([ 5, 20])>
<tf.Variable 'Variable:0' shape=(2,) dtype=int32, numpy=array([10, 60])>

tensor张量转numpy

tensor数据自带转换np的方法

a = tf.constant([[1.0, 2.0], [3.0, 4.0]])
print(a.numpy())

张量和np数据都可以作为彼此函数或算子的输入参数

a = tf.constant([[1, 2, 3], [4, 5, 6]])
b = np.array([[1, 2, 3], [4, 5, 6]])
c = tf.add(a,b)
d = np.add(a,b)
print(c,"\n",d)

tf.Tensor(
[[ 2  4  6]
 [ 8 10 12]], shape=(2, 3), dtype=int32) 
 [[ 2  4  6]
 [ 8 10 12]]

神经网络正向传播和反向传播的理解

网络间的数据传播与矫正分为三步

1.输入的x数据经过神经元的权重（w）和偏置（b）所进行的矩阵计算，我们假定他的计算结果输出是z，
$$z=wx+b$$
2.上一步的z需要经过激活函数，这边的y简单理解就是网络的预测值
$$y=\sigma (z)$$
3.损失函数loss，（其实就是用各种公式去比较网络的输出和实际输出，最简单的就是标准差）
$$loss=l（y）$$
常见的损失函数

正向传播

经过上面的前两步就可以出结果

反向传播

最终的目的是让偏导结果趋于0
$$\frac{\partial (loss)}{\partial (w)}=\frac{\partial (loss)}{\partial (y)}\ast \frac{\partial (y)}{\partial (z)}\ast \frac{\partial (z)}{\partial (w)}$$
正好对应上面说的三个部分，对损失函数的偏导，对激发函数的偏导，对矩阵计算的偏导

根据数学知识，在已知实际y和预测y的前提下，因为是对单一w求偏导，其他w都视为常量，可以把偏导目标简化为一次函数
$$loss(w)=kw+b$$
这样理解的话就是
偏导结果k>0,w的函数增，且loss>0,w要尽量的小，loss才能向0收敛
偏导结果k<0,w的函数减，且loss>0,w要尽量的大，loss才能向0收敛

w的更新，引出学习率a (a>0)
$$w=w+a\ast \Delta w$$

激活函数

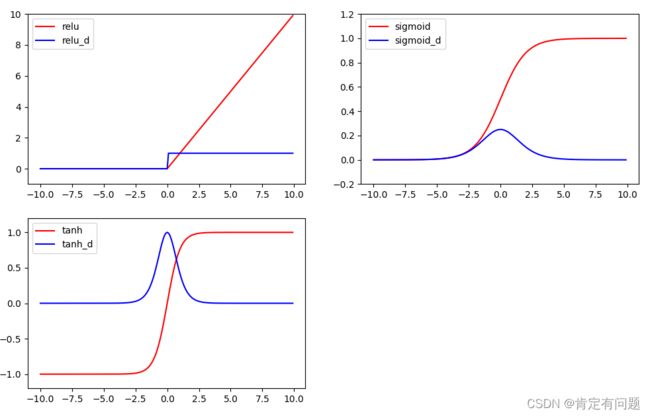
1.tanh和sigmoid随着自变量变大，导数趋于0，
2.relu小于0的部分，存在数据损失。

1.常见激活函数的图形（relu，sogmoid，tanh，。。。）

import math
import numpy as np


# 做一些假数据来观看图像
x_np = np.arange(-10, 10, 0.1)
x = np.arange(-10, 10, 0.1)

# 几种常用的 激励函数
y_relu = np.where(x < 0, 0, x)
y_sigmoid = 1 / (1 + math.e ** (-x))
y_tanh = (math.e ** (x) - math.e ** (-x)) / (math.e ** (x) + math.e ** (-x))

y_relu_d = np.where(x < 0, 0, 1)
y_sigmoid_d = 1 / (2 + math.e ** (-x)+ math.e ** (x))
y_tanh_d = 1-y_tanh*y_tanh
# y_softmax = F.softmax(x)  softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类

import matplotlib.pyplot as plt

plt.figure(1, figsize=(8, 6))
plt.axis('on')
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.plot(x_np, y_relu_d, c='blue', label='relu_d')
plt.ylim((-1, 10))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.plot(x_np, y_sigmoid_d, c='blue', label='sigmoid_d')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.plot(x_np, y_tanh_d, c='blue', label='tanh_d')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

# plt.subplot(224)
# plt.plot(x_np, y_softplus, c='red', label='softplus')
# plt.ylim((-0.2, 6))
# plt.legend(loc='best')

plt.show()