用于数字病理学的旋转等变CNN
我 们 演 示 了 2 层 G − C N N 如 何 在 p 4 中 等 变 。 显 示 了 每 层 一 个 核 的 特 征 图 , 蓝 色 虚 线 箭 头 表 示 两 个 输 入 的 如 何 对 应 。 我们演示了 2 层 G-CNN 如何在 p4 中等变。显示了每层一个核的特征图,蓝色虚线箭头表示两个输入的如何对应。 我们演示了2层G−CNN如何在p4中等变。显示了每层一个核的特征图,蓝色虚线箭头表示两个输入的如何对应。
Z 2 − ( 4 r o t a t e d v e r s i o n s o f t h e s a m e k e r n e l ) − > P 4 P 4 − ( t h e p 4 − k e r n e l , c y c l i c a l l y − s h i f t i n g a n d r o t a t i n g t h e k e r n e l f o r e a c h o r i e n t a t i o n ) − > P 4 最 后 一 层 演 示 了 方 向 上 的 平 均 池 化 如 何 产 生 局 部 不 变 且 全 局 等 变 的 表 示 p 4 上 的 全 局 平 均 池 化 将 导 致 表 示 对 平 移 和 旋 转 全 局 不 变 。 Z2-(4 rotated versions of the same kernel)->P4\\ P4-(the p4-kernel, cyclically-shifting and rotating the kernel for each orientation)->P4 \\ 最后一层演示了方向上的平均池化如何产生局部不变且全局等变的表示\\ p4 上的全局平均池化 将导致表示对平移和旋转全局不变。 Z2−(4rotatedversionsofthesamekernel)−>P4P4−(thep4−kernel,cyclically−shiftingandrotatingthekernelforeachorientation)−>P4最后一层演示了方向上的平均池化如何产生局部不变且全局等变的表示p4上的全局平均池化将导致表示对平移和旋转全局不变。
上面这个图表示的是经过旋转之后的图片,输出的feature map具有等变性。
通过debug pytorch的代码,能够了解具体操作的过程是,Z2-P4卷积是将kernel旋转四次,分别与输入的图片做卷积,而P4-P4卷积是对于输出的4个feature map,分别将四个kernel绕着顺时针方向转动90°,同时kernel自身也转动90°,这样的四种状态分别与输出的不动的feature map分别做卷积,每一种状态做卷积之后的输出结果四个相加,这样为一个featuremap,四个状态对应4个feature map,即为最终的输出,那这样又为什么会学习到一个旋转不变的性质呢?因为同一个kernel的四种状态对于不同的feature map应该是能够得到一个p4的约束,所以能够学习到一个旋转等变的性质
博客园

我们提出了一种新的数字病理分割模型,基于观察到组织病理学图像在旋转和反射下本质上是对称的。 利用最近关于旋转等变 CNN 的发现,所提出的模型以有原则的方式利用了这些对称性。 我们提出了一个可视化分析,显示了预测稳定性的提高,并证明利用旋转等方差显着提高了具有挑战性的淋巴结转移数据集的肿瘤检测性能。 我们进一步提出了一个新的派生数据集,以结合初始基准对机器学习模型进行原则性比较。 通过这个数据集,组织病理学诊断的任务可以作为基础机器学习研究的一个具有挑战性的基准。
我们提出了一个完全卷积的斑块分类模型,该模型与90◦ 旋转和反射,使用[5]提出的方法。我们在Camelyon16基准[9]上对模型进行了评估,结果表明,在玻片分级和肿瘤定位任务方面,该模型明显优于可比CNN。
这项工作的贡献如下:(1)我们提出了一种利用组织病理学固有对称性的新型深度学习模型,(2)证明旋转等方差提高了模型的可靠性,以及(3)提出了一个新的大规模组织病理学数据集,使 精确的模型评估。
Z 2 群 不 是 这 个 Z 2 群 Z^2群不是这个Z_2群 Z2群不是这个Z2群
- Cohen, T.S., et al.: Group equivariant convolutional networks. (2016)
- Worrall, D.E., et al.: Harmonic networks: Deep translation and rotation equivariance. In: Proc. IEEE CVPR. Volume 2., openaccess.thecvf.com (2017)
- Weiler, M., et al.: Learning steerable filters for rotation equivariant CNNs. (2017)
y ( n ) = x ( n ) ∗ h ( n ) = ∑ − ∞ + ∞ x ( i ) h ( n − i ) y(n)=x(n)*h(n)=\sum_{-\infty}^{+\infty}x(i)h(n-i) y(n)=x(n)∗h(n)=−∞∑+∞x(i)h(n−i)
等变
平 移 不 变 性 \color{blue}平移不变性 平移不变性:将图片平移后再送入若干卷积层得到的结果,与将原图直接送入相同卷积层得到结果后再对特征图进行平移所得到的结果一样。
如果一个函数满足,输入改变而输出也以同样的方式改变的这一性质,我们就说它是等变的。
若 f ( L g ( x ) ) = L g ( f ( x ) ) , L g 为 群 元 g 对 应 的 算 符 , 称 f ( x ) 对 于 变 换 g 等 变 。 且 有 : [ L g f ] ( x ) = [ f ∗ g − 1 ] ( x ) = f ( g − 1 x ) 若f(L_g(x))=L_g(f(x)),L_g为群元g对应的算符,称f(x)对于变换g等变。\\ 且有:[L_gf](x)=[f*g^{-1}](x)=f(g^{-1}x) 若f(Lg(x))=Lg(f(x)),Lg为群元g对应的算符,称f(x)对于变换g等变。且有:[Lgf](x)=[f∗g−1](x)=f(g−1x)
如 上 式 中 g = x + t , 则 g − 1 = x − t , 只 需 计 算 在 x − t ( 左 平 移 ) 的 特 征 图 , 就 能 得 到 x 的 特 征 图 右 平 移 的 结 果 。 如上式中g=x+t,则g^{-1}=x-t,只需计算在x-t(左平移)的特征图,\\就能得到x的特征图右平移的结果。 如上式中g=x+t,则g−1=x−t,只需计算在x−t(左平移)的特征图,就能得到x的特征图右平移的结果。
卷积
多 通 道 卷 积 f : Z 2 → R K l 多通道卷积f:Z^2\rightarrow R^{K^l} 多通道卷积f:Z2→RKl
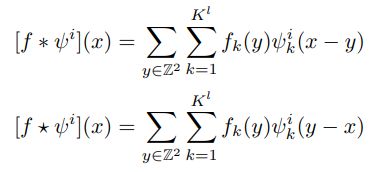
上 面 的 式 子 表 示 卷 积 , 下 面 的 式 子 表 示 相 关 ( c o r r e l a t i o n ) , 两 者 应 用 于 C N N 时 从 训 练 结 果 上 讲 是 等 价 的 。 x 表 示 坐 标 , y 表 示 的 是 特 定 的 平 移 操 作 , f 表 示 特 征 图 , l 表 示 第 l 层 K l 表 示 通 道 数 , ψ 表 示 卷 积 核 , 上 式 表 现 了 一 个 卷 积 核 ψ 在 特 征 图 上 卷 积 的 过 程 。 相 关 是 通 过 移 动 卷 积 核 , 然 后 与 特 征 图 计 算 点 积 来 计 算 的 。 上面的式子表示卷积,下面的式子表示相关(correlation),\\\href{https://blog.csdn.net/heiha1232/article/details/89072315}{两者应用于CNN时从训练结果上讲是等价的。}\\ x表示坐标,y表示的是特定的平移操作,f表示特征图,l表示第l 层\\ K^l 表示通道数,\psi表示卷积核,上式表现了一个卷积核\psi在特征图上卷积的过程。\\ 相关是通过移动卷积核,然后与特征图计算点积来计算的。 上面的式子表示卷积,下面的式子表示相关(correlation),两者应用于CNN时从训练结果上讲是等价的。x表示坐标,y表示的是特定的平移操作,f表示特征图,l表示第l层Kl表示通道数,ψ表示卷积核,上式表现了一个卷积核ψ在特征图上卷积的过程。相关是通过移动卷积核,然后与特征图计算点积来计算的。
平移不变性
L t 表 示 进 行 位 移 t 的 变 换 , 上 式 表 明 : 先 对 特 征 图 f 进 行 位 移 t 的 变 换 , 再 通 过 卷 积 核 ψ 提 取 特 征 , ⇔ : 先 通 过 卷 积 核 ψ 提 取 特 征 , 再 进 行 位 移 t 的 变 换 。 由 此 , 得 到 位 移 不 变 性 。 L_t 表示进行位移t的变换,上式表明:\\先对特征图f进行位移t的变换,再通过卷积核 \psi 提取特征,\\ \Leftrightarrow:先通过卷积核 \psi 提取特征,再进行位移t的变换。\\由此,得到位移不变性。 Lt表示进行位移t的变换,上式表明:先对特征图f进行位移t的变换,再通过卷积核ψ提取特征,⇔:先通过卷积核ψ提取特征,再进行位移t的变换。由此,得到位移不变性。
传统卷积无旋转不变性
作者发现旋转操作与卷积操作是不対易的。
若 对 特 征 图 进 行 旋 转 之 后 , 再 进 行 卷 积 , 应 该 ⇔ : 特 征 图 直 接 与 卷 积 核 卷 积 , 再 进 行 旋 转 实 际 ⇔ : 对 卷 积 核 做 反 向 的 旋 转 , 再 对 原 始 特 征 图 进 行 卷 积 , 再 把 卷 积 得 到 的 结 果 旋 转 回 去 。 若对特征图进行旋转之后,再进行卷积,\\ 应该\Leftrightarrow: 特征图直接与卷积核卷积,再进行旋转 \\ 实际\Leftrightarrow:对卷积核做反向的旋转,再对原始特征图进行卷积,再把卷积得到的结果旋转回去。 若对特征图进行旋转之后,再进行卷积,应该⇔:特征图直接与卷积核卷积,再进行旋转实际⇔:对卷积核做反向的旋转,再对原始特征图进行卷积,再把卷积得到的结果旋转回去。
实际


假设我们定义一个新的卷积操作:
[ f ⋄ ψ i ] ( θ ) = ∑ y ∈ Z 2 ∑ k = 1 K l f k ( y ) ψ k i ( A θ − 1 y ) 其 中 , A θ 表 示 旋 转 角 度 为 θ 的 旋 转 矩 阵 [ f ⋄ ψ^i ] ( θ ) = ∑_{y ∈ Z^2} ∑_{k = 1}^ {K l} f_k ( y ) ψ_k^i ( A_θ^{− 1} y )\\ 其中,A_θ 表示旋转角度为θ的旋转矩阵 [f⋄ψi](θ)=y∈Z2∑k=1∑Klfk(y)ψki(Aθ−1y)其中,Aθ表示旋转角度为θ的旋转矩阵
根据这个卷积操作,推导旋转不变性:
[ [ L r f ] ⋄ ψ ] ( θ ) = ∑ y f ( A r y ) ψ ( A θ − 1 y ) = ∑ y f ( y ) ψ ( A r − 1 A θ − 1 y ) = ∑ y f ( y ) ψ ( A ( θ + r ) − 1 y ) = L r [ f ⋄ ψ ] ( θ ) [ [ L_r f ] ⋄ ψ ] ( θ ) = ∑_y f ( A_r y ) ψ ( A_θ^{ − 1} y ) \\ = ∑_y f ( y ) ψ ( A_r^{ − 1} A_θ^{− 1} y ) \\= ∑_y f ( y ) ψ ( A_{( θ + r ) }^{− 1} y ) = L_r [ f ⋄ ψ ] ( θ ) [[Lrf]⋄ψ](θ)=y∑f(Ary)ψ(Aθ−1y)=y∑f(y)ψ(Ar−1Aθ−1y)=y∑f(y)ψ(A(θ+r)−1y)=Lr[f⋄ψ](θ)
其 中 , A r 表 示 旋 转 矩 阵 其中,A _r 表示旋转矩阵 其中,Ar表示旋转矩阵
相关计算是通过移动滤波器,然后用特征图计算点积来计算的。通过将移位替换为某个G组的更一般变换,我们得到了G-CNN第一层中使用的G相关性:

注意,输入图像f和滤波器ψ都是平面 Z 2 Z^2 Z2的函数,但特征映射 f ∗ ψ f*ψ f∗ψ是离散群G上的函数(可能包含作为子群的平移)。因此,对于第一层之后的所有层,滤波器ψ也必须是G上的函数,并且相关运算变为

G − C N N 推 广 了 对 f e a t u r e − m a p 的 变 换 操 作 , 从 传 统 的 只 有 平 移 变 换 的 群 Z 2 到 某 个 对 称 性 群 G 。 而 且 推 广 以 后 , G − C N N 卷 积 层 对 于 该 群 的 对 称 性 变 换 操 作 具 有 等 变 性 质 。 当 对 称 性 群 G 只 有 平 移 一 种 对 称 性 操 作 , 则 G − C N N 也 就 是 传 统 的 C N N G-CNN推广了对feature-map的变换操作,从传统的只有平移变换的群Z^2 到某个对称性群 G 。\\ 而且推广以后,G-CNN卷积层对于该群的对称性变换操作具有等变性质。\\ 当对称性群G只有平移一种对称性操作,则G-CNN也就是传统的CNN G−CNN推广了对feature−map的变换操作,从传统的只有平移变换的群Z2到某个对称性群G。而且推广以后,G−CNN卷积层对于该群的对称性变换操作具有等变性质。当对称性群G只有平移一种对称性操作,则G−CNN也就是传统的CNN
如果任何变换 g ∈ G 可以分解为平移 t ∈ Z^2 和原点稳定器中的变换 s(即 s 离开原点不变),则平面对称群 G 称为分裂。 对于 p4 组,我们可以写 g = ts 表示 t 是平移,s 是绕原点的旋转,而 p4m 分为平移和旋转翻转。 使用 G 的这种分裂以及 L_gL_h = Lgh 的事实,我们可以将 G 相关性(等式 10 和 11)改写如下:

对 于 某 一 个 g , h 一 直 是 p 4 群 , 不 会 改 变 。 因 而 公 式 中 的 g − 1 h 其 实 就 是 一 个 左 陪 集 。 对于某一个g ,h 一直是p4群,不会改变。因而公式中的 {{g^{ - 1}}h}其实就是一个左陪集。 对于某一个g,h一直是p4群,不会改变。因而公式中的g−1h其实就是一个左陪集。
ψ k ( g − 1 h ) 的 意 思 是 , 一 个 集 合 里 有 k = 4 干 张 滤 波 器 图 像 {\psi _k}\left( {{g^{ - 1}}h} \right)的意思是,一个集合里有k=4干张滤波器图像 ψk(g−1h)的意思是,一个集合里有k=4干张滤波器图像
它 们 之 间 能 在 群 g − 1 h 下 互 相 转 换 它们之间能在群 {g^{ - 1}}h下互相转换 它们之间能在群g−1h下互相转换
f k ( h ) ψ k ( g − 1 h ) 。 由 于 ψ k ( g − 1 h ) 是 16 张 图 , 那 么 要 执 行 “ 乘 积 ” , f k ( h ) 也 需 要 复 制 出 16 张 图 , 把 二 者 一 一 对 应 , “ 重 叠 ” 在 一 起 , 做 点 积 。 f_k(h)ψ_k(g^{ - 1}h)。由于 {\psi _k}\left( {{g^{ - 1}}h} \right)是16张图,那么要执行“乘积”,\\ {f_k}(h)也需要复制出16张图,把二者一一对应,“重叠”在一起,做点积。 fk(h)ψk(g−1h)。由于ψk(g−1h)是16张图,那么要执行“乘积”,fk(h)也需要复制出16张图,把二者一一对应,“重叠”在一起,做点积。

where X = Z^2 in layer one and X = G in further layers
因此,为了计算 p4(或 p4m)相关 f ⋆ ψ,我们可以首先计算L_sψ(“滤波器变换”)
所有四个旋转(或所有八个旋转翻转)的 ,然后在 f 和增强的 滤波器组。
逐点非线性
至此,文章定义了G-CNN的核心概念,接下来的部分是从理论上处理非线性和pooling。对于非线性操作,结论是非线性操作与群变换対易,仍然保留等变性质
回想一下,我们将特征图视为 G 上的函数。在此观点中,将非线性 ν : R → R 应用于特征图相当于函数组合。

由于左变换算子 L 通过预组合起作用,因此 C 和 L 交换

破欧玲
为了简化分析,我们将池化操作分为两步:池化本身(无跨步执行)和子采样步骤。
应用于特征映射 f : G → R 的非跨步 maxpooling 操作可以建模为一个操作符 P,它作用于 f 为

其中 gU = {gu | u ∈ U} 是某个池域 U ⊂ G(通常是恒等变换的邻域)的 g 变换。 在常规的 convnet 中,U 通常是包含原点 (0, 0) 的 2 × 2 或 3 × 3 正方形,g 是平移。
如补充材料所示,pooling与Lh commute:

在 G-CNN 中,“步幅”的概念是通过对子群 H ⊂ G 进行xia采样来概括的。也就是说,H 是 G 的一个子集,它本身就是一个群(即在乘法和逆运算下封闭)。 子采样的特征图然后等变到 H 但不是 G
在标准的 convnet 中,步幅为 2 的池化
与池化然后在 H 上进行子采样相同
H = {(2i, 2j)|(i, j) ∈ Z 2}
![]()
对于 p4-CNN,我们可以对包含所有 4 个旋转以及 2 个像素倍数的移位的子组 H 进行子采样。
我们可以通过选择我们的池化区域 U 作为子群 H ⊂ G 来获得完全的 G 等方差。在群论中,由此产生的池化域 gH 被称为陪集。 陪集将组划分为不重叠的区域。 由陪集池化产生的特征图对于 H 的右动作是不变的,因为陪集同样是不变的 (ghH = gH)。 因此,我们可以任意选择一个陪集代表对每个陪集进行子采样
陪集池化产生的特征图可以被认为是商空间 G/H 上的函数,其中如果两个变换与 H 中的变换相关,则认为它们是等价的。
例如,在 p4 特征图中,我们可以在每个空间位置(围绕原点旋转的子组 R 的陪集)的所有四个旋转上进行池化。 生成的特征图是 Z 2 ∼= p4/R 上的函数,即它将以与输入图像相同的方式进行变换。 另一个例子是 Z 上的特征映射,我们可以将移位子组 nZ 的陪集池化为 n 的倍数。 这给出了 Z/nZ 上的特征图,其在平移下具有循环变换规律。
我们对 G-CNN 的分析到此结束。 由于所有层类型都是等变的,我们可以自由地将它们堆叠到深度网络中,并期望 G-conv 参数共享在任意深度都有效。
以上是理论分析,但是具体如何在程序中实现这种看似复杂的池化,文中没有细化。如果有了解细节的朋友,还望告知。
我 们 将 基 线 架 构 的 所 有 卷 积 层 替 换 为 p 4 或 p 4 m 卷 积 。 对 于 恒 定 数 量 的 过 滤 器 , 这 会 使 特 征 图 的 大 小 增 加 4 或 8 倍 , 从 而 又 增 加 了 下 一 层 中 每 个 过 滤 器 所 需 的 参 数 数 量 。 因 此 , 我 们 将 每 个 p 4 − c o n v 层 中 的 过 滤 器 数 量 减 半 , 然 后 将 除 以 每 个 p 4 m − c o n v 层 中 的 。 这 样 , 参 数 的 数 量 几 乎 不 变 , 而 内 部 表 示 的 大 小 却 增 加 了 。 我们将基线架构的所有卷积层替换为p4或p4m卷积。对于恒定数量的过滤器,这会使特征图的大小增加4或8倍,从而又增加了下一层中每个过滤器所需的参数数量。因此,我们将每个p4-conv层中的过滤器数量减半,然后将除以每个p4m-conv层中的。这样,参数的数量几乎不变,而内部表示的大小却增加了。 我们将基线架构的所有卷积层替换为p4或p4m卷积。对于恒定数量的过滤器,这会使特征图的大小增加4或8倍,从而又增加了下一层中每个过滤器所需的参数数量。因此,我们将每个p4−conv层中的过滤器数量减半,然后将除以每个p4m−conv层中的。这样,参数的数量几乎不变,而内部表示的大小却增加了。
遵 循 G o o d f e l l o w 等 人 的 观 点 , + 表 示 使 用 水 平 翻 转 和 少 量 平 移 进 行 适 度 的 数 据 增 强 遵循Goodfellow等人的观点,+表示使用水平翻转和少量平移进行适度的数据增强 遵循Goodfellow等人的观点,+表示使用水平翻转和少量平移进行适度的数据增强
参考:
0.Group Equivariant Convolutional Networks
1.G-CNN:群CNN
作者在带有旋转变换的MNIST和CIFAR数据上进行了实验,证实旋转群CNN能较好地抗旋转。
许多经验及实验都验证了:卷积权值共享(convolutional weight sharing)和网络深度(depth)对于神经网络的效果起到了重要作用。
卷积权值共享依赖于任务中的平移不变性:预测标签的函数和数据分布对于平移变换都近似于不变。
CNN中已经具有了平移不变性,这篇论文的工作是将神经网络拓展到更大的群上,引入更多的对称性,如旋转(rotation)和反射(reflection)
文中引入了两个群对核进行扩充,形成核的库,一个是p4群(SE(2)旋转单次90度,平移单次整数),另一个是p4m群(p4+反射)。
新的卷积公式,把对核的操作考虑进去。
作者提到,互相关和卷积公式实际上并不一样,如果在前向传播的过程中采用了互相关公式进行卷积操作,那么在后向回传的时候就会涉及到卷积公式,反之亦然。很多资料将这两种统统称为卷积,作者这里提出他们之间的区别是为了证明不管前向还是后向,卷积均满足等变性。
接下来,对于神经网络中三种经典的层:卷积层、池化层和非线性层,作者一一证明了其跟这种核的群变换都是可以互换的,也就是可以保持等变性。作者认为,池化的作用在于对特征图进行下采样进而减少变量。这里的池化分成不带步幅的池化以及对池化后的特征图进行下采样。在群中,如果一部分群元素可以满足群的定义,那么就称为原来的群的子群。对子群进行变换,可以得到陪集,也就是子群的子区域。陪集将原来的群划分为互不重叠的区域。由于对陪集进行池化得到的特征图不会随着子群不同的变换而改变,也就是尽管陪集的表示有不同方式,但可以对任意一个陪集的表示进行下采样,原文称之为陪集池化。原文中给出如下例子。对于一个满足p4对称性(平移对称性和旋转90°的对称性)的特征图,我们以涉及到旋转操作的子群作为池化域,对空间中每个点关于四度旋转(90°,180°,270°,360°)各做一次池化,还有一次关于平移变换的池化。对应下采样的特征图跟下采样的子群等变而跟大群不等变,但是对特征图的分析总是将整个特征图的所有通道结合起来的,结合后的特征图跟原来的群依然等变。于是有望在深层神经网络中用新的卷积方式替换原来的卷积操作,使得参数共享在任意深度均可以发挥作用。G-CNN实现。
shixian
https://github.com/parasdahal/group-equivariant-autoencoder
添加链接描述
transformation invariant pooling (TI-Pooling)

https://geometricdeeplearning.com/
https://github.com/e3nn/e3nn