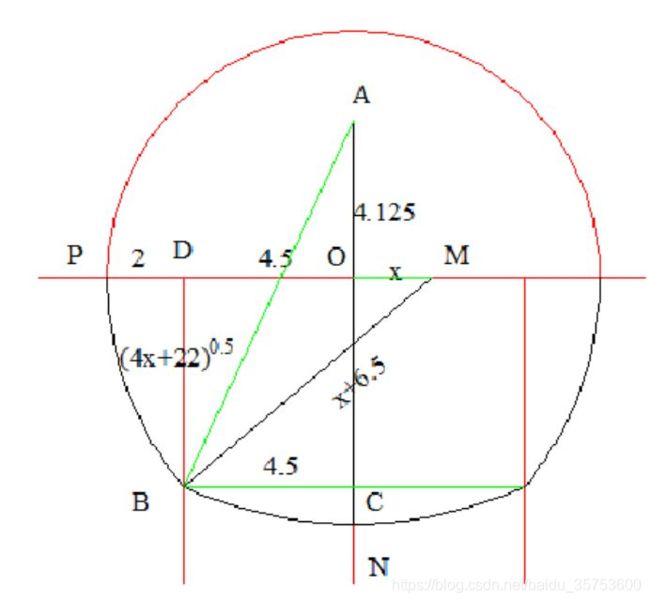
四心圆马蹄形隧道画法
<div id="CanvasWrap" style=" background:#fff; width: 600px; height: 600px; border: 1px solid black;"></div>
<script src="complexNum.js"></script>
<script src="complexConst.js"></script>
<script src="angleUtils.js"></script>
<script src="formulaUtils.js"></script>
<script type="text/javascript">
//
var canvas, context;
var div = document.getElementById("CanvasWrap");
div.innerHTML = "";
canvas = document.createElement("canvas");
canvas.style.width = "600px"
canvas.style.height = "600px"
canvas.width = 600;
canvas.height = 600;
context = canvas.getContext("2d");
div.appendChild(canvas);
function execDraw()
{
var centerPoint = { x: 250, y: 350 };
// 上部圆的半径
var upRadius = 200;
// 画:四心圆马蹄形隧道
drawTunnel(centerPoint, upRadius);
upRadius = 180;
var color = "yellow";
drawTunnel(centerPoint, upRadius, color);
};
function clearCanvas()
{
context.clearRect(0, 0, 600, 600);
};
function drawTunnel(centerPoint, upRadius, paramColor) {
var color = "blue";
if (arguments.length > 2) {
color = paramColor;
}
context.lineWidth = 1.1;
context.strokeStyle = color;
// 绘制上部半圆
context.beginPath();
// 逆时针绘制:true
var counterclockwise = true;
context.save();
context.translate(centerPoint.x, centerPoint.y);
context.arc(0, 0, upRadius, 0, Math.PI, counterclockwise);
context.stroke();
context.restore();
context.closePath();
// 绘制下部弧度,5 * PI/18 = 50度
context.beginPath();
// 逆时针绘制:false
counterclockwise = false;
context.save();
context.translate(centerPoint.x, centerPoint.y);
context.arc(0, -110, upRadius + 110, 6.5 * Math.PI / 18, 11.5 * Math.PI / 18, counterclockwise);
context.stroke();
context.restore();
context.closePath();
// 绘制左下部弧度
context.strokeStyle = color;
context.beginPath();
// 逆时针绘制:true
counterclockwise = true;
// 求圆点的位置
var lenAO = 110;
var lenON = upRadius;
var lenOP = upRadius;
var lenAB = upRadius + 110;
// 25度
var angleBottom = 2.5 * Math.PI / 18;
var lenBC = lenAB * Math.sin(angleBottom);
var lenOD = lenBC;
// 三角形DBM
// lenDB ^ 2 = lenBM^2 - (lenOD + lenOM)^2
// lenBM = lenOM + lenOP
// lenDB = sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2)
// lenDB = lenOC
// lenAC = lenAO + lenOC
// lenAC = lenAO + lenDB
// lenAC = lenAO + sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2)
// 三角形ABC
// lenAC ^ 2 + lenBC ^ 2 = lenAB ^ 2
// (lenOM + lenOP)^2 - (lenOD + lenOM)^2 + lenAO^2 + 2 * lenAO * sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2) + lenBC ^ 2 = lenAB ^ 2
// 2 * lenOP * lenOM - 2 * lenOD * lenOM + 2 * lenAO * sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2) = lenAB ^ 2 - lenBC ^ 2 + lenOD^2 - lenOP^2 - lenAO^2
// constA = (lenAB ^ 2 - lenBC ^ 2 + lenOD^2 - lenOP^2)
// constB = (2 * lenOP - 2 * lenOD)
// (2 * lenOP - 2 * lenOD)* lenOM - (lenAB ^ 2 - lenBC ^ 2 + lenOD^2 - lenOP^2) = - 2 * lenAO * sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2)
// constB * lenOM - constA = - 2 * lenAO * sqrt((lenOM + lenOP)^2 - (lenOD + lenOM)^2)
// constB^2 * lenOM^2 + constA^2 - 2 * constA * constB * lenOM
// = 4 * lenAO^2 * ( lenOP ^2 + 2 * lenOP * lenOM - lenOD ^2 - 2 * lenOD * lenOM )
// = 4 * lenAO^2 * ( lenOP ^2 - lenOD ^2 + (2 * lenOP - 2 * lenOD)* lenOM )
// constC = lenOP ^2 - lenOD ^2
// = 4 * lenAO^2 * ( constC + constB * lenOM)
// constB^2 * lenOM^2 - (2 * constA * constB + 4 * lenAO^2 * constB) * lenOM + constA^2 - 4 * lenAO^2 * constC = 0
var constA = Math.pow(lenAB, 2) - Math.pow(lenBC, 2) + Math.pow(lenOD, 2) - Math.pow(lenOP, 2) - Math.pow(lenAO, 2);
var constB = (2 * lenOP - 2 * lenOD);
var constC = Math.pow(lenOP, 2) - Math.pow(lenOD, 2);
var coefficient2 = Math.pow(constB, 2);
var coefficient1 = - 2 * constA * constB - 4 * Math.pow(lenAO, 2) * constB;
var constFormula = Math.pow(constA, 2) - 4 * Math.pow(lenAO, 2) * constC;
var result = FormulaUtil.calcSquareFormulaZero(coefficient2, coefficient1, constFormula);
console.log(result.length);
var lenOM = 0;
if (result.length > 0) {
if (result[0].real > 0 && result[0].real < lenOP) {
lenOM = result[0].real;
} else if (result.length > 1 && result[1].real > 0 && result[1].real < lenOP) {
lenOM = result[1].real;
}
}
var testRst = coefficient2 * Math.pow(lenOM, 2) + coefficient1 * lenOM + constFormula
var lenDM = lenOM + lenOD;
var lenBM = lenOM + lenOP;
var sideAngle = AngleUtil.getCosDeg(lenDM / lenBM);
context.save();
context.translate(centerPoint.x, centerPoint.y);
context.arc(lenOM, 0, upRadius +lenOM, Math.PI, Math.PI - sideAngle * Math.PI / 180 , counterclockwise);
context.stroke();
context.restore();
context.closePath();
// 绘制右下部弧度
context.strokeStyle = color;
// 绘制右下部弧度
context.beginPath();
// 逆时针绘制:false
counterclockwise = false;
context.save();
context.translate(centerPoint.x, centerPoint.y);
context.arc(-lenOM, 0, upRadius +lenOM, 0, sideAngle * Math.PI / 180 , counterclockwise);
context.stroke();
context.restore();
context.closePath();
}
// ]]>
</script>
<p>
<br />
<button onclick="execDraw();" type="button">执行</button>
<button onclick="clearCanvas();" type="button">清理</button>
</p>
附属添加js文件
complexConst.js
/**
* ref: https://blog.csdn.net/iloveas2014/article/details/83478737
*
*/
function ComplexConsts()
{
}
/**
* OMEGA是模为1,幅角主值等于120度的复数,它是1开三次方的结果,在解3次和4次方程中非常常用
* OMEGA就是希腊字母里最像w的那个
*
*/
ComplexConsts.OMEGA = new ComplexNum(1 / 2, Math.sqrt(3) / 2);
/**
* 理论上OMEGA的平方可以用两个OMEGA相乘得到,但由于容易产生浮点误差,加上数值固定,因此也直接做成常量
*
*/
ComplexConsts.OMEGA_SQUARE = new ComplexNum(1 / 2, Math.sqrt(3) / 2);
/**
* OMEGA的3次方恰好等于实数1,就最好不要再自己用三个OMEGA来相乘了
*
*/
ComplexConsts.OMEGA_CUBIC = new ComplexNum(1, 0);
/**
* OMEGA的0次方,纯属为了让代码清晰而定义的常量
*
*/
ComplexConsts.OMEGA_ZERO = new ComplexNum(1, 0);
/**
* 虚数单位i
*
*/
ComplexConsts.I = new ComplexNum(0, 1);
complexNum.js
/**
* ref: https://blog.csdn.net/iloveas2014/article/details/83478737
*
*/
function ComplexNum(real, image)
{
this.real = isNaN(real) ? 0 : real;
this.image = isNaN(image) ? 0 : image;
/**
* 设置复数的值
* @param reala 复数的实部
* @param imagea 复数的虚部
*
*/
function setTo(reala, imagea)
{
this.real = reala;
this.image = imagea;
}
this.setTo = setTo;
/**
* 复数相加
* @param complex 要与其相加的复数
* @return
*
*/
function add(complex)
{
return new ComplexNum(this.real + complex.real, this.image + complex.image);
}
this.add = add;
/**
* 为了使用上方便一点,此处加上与实数相加的方法
* @param num 要与其相加的数字
* @return
*
*/
function addNumber(num)
{
return new ComplexNum(this.real + num, this.image);
}
this.addNumber = addNumber;
/**
* 复数相减
* @param complex 要与其相减的复数
* @return
*
*/
function subtract(complex)
{
return new ComplexNum(this.real - complex.real, this.image - complex.image);
}
this.subtract = subtract;
/**
* 为了使用上方便一点,此处加上与实数相减的方法
* @param num 要与其相减的数字
* @return
*
*/
function subtractNumber(num)
{
return new ComplexNum(this.real - num, image);
}
this.subtractNumber = subtractNumber;
/**
* 复数乘法 (运算法则是利用多项式乘法进行展开得到)
* @param complexNum 要与其相乘的复数
* @return
*
*/
function multiply(complexNum)
{
return new ComplexNum(this.real * complexNum.real - this.image * complexNum.image, this.image * complexNum.real + this.real * complexNum.image);
}
this.multiply = multiply;
/**
* 为了使用上方便一点,此处加上与实数相乘的方法
* @param num 要与其相乘的数字
* @return
*
*/
function multiplyNumber(num)
{
return new ComplexNum(this.real * num, this.image * num);
}
this.multiplyNumber = multiplyNumber;
/**
* 复数除法 (运算法则是通过平方差公式,分子分母同时乘以分母的共轭复数以去除分母中的虚部,然后就利用乘法法则进行计算)
* @param complexNum 要与其相除的复数
* @return
*
*/
function divide(n)
{
//分母化为实数
var denominator = n.real * n.real + n.image * n.image;
//分子也乘以同样的复数,并除以分母即得最终结果
return new ComplexNum((this.real * n.real + this.image * n.image) / denominator, (this.image * n.real - this.real * n.image) / denominator);
}
this.divide = divide;
/**
* 为了使用上方便一点,此处加上与实数相除的方法
* @param num 要与其相除的数字
* @return
*
*/
function divideNumber(num)
{
return new ComplexNum(this.real / num, this.image / num);
}
this.divideNumber = divideNumber;
/**
* 开平方运算
* @return
*
*/
function squareRoot()
{
return this.getRoot(2);
}
this.squareRoot = squareRoot;
/**
* 开立方运算
* @return
*
*/
function cubicRoot()
{
return this.getRoot(3);
}
this.cubicRoot = cubicRoot;
/**
* 开任意整数次方的运算
* @param times
* @return
*
*/
function getRoot(times)
{
var vec = [];
//复数开方运算的原理是把辐角根据次数进行平分
var degree = this.degree;
degree /= times;
//然后多个方根平分360度,所以需要算出每个方根之间的辐角间隔
var degreeUnit = 360 / times;
//复数长度(模)直接开方即可
var lengthRoot = Math.pow(this.length, 1 / times);
var cosDic = AngleUtil.getCosDic();
var sinDic = AngleUtil.getSinDic();
//然后就能通过循环生成所有开方结果
for(var i = 0; i < times; i ++)
{
var currentDegree = (degree + i * degreeUnit);
var currentAngle = currentDegree * Math.PI / 180;
var cos = isNaN(cosDic[currentDegree]) ? Math.cos(currentAngle) : cosDic[currentDegree];
var sin = isNaN(sinDic[currentDegree]) ? Math.sin(currentAngle) : sinDic[currentDegree];
//trace(lengthRoot * cos, lengthRoot * sin);
vec.push(new ComplexNum(lengthRoot * cos, lengthRoot * sin));
}
return vec;
}
this.getRoot = getRoot;
/**
* 复数的辐角主值(复数所在点与坐标连线跟水平线的夹角),以弧度为单位
* 必要时可用degree属性可以更有效避免边缘位置的浮点误差引发的错误
* @see degree()
*
*/
Object.defineProperty(this, "angle", {get: getAngle});
function getAngle()
{
//由于复数开方基于角度,所以一旦有浮点误差就会导致角度在边缘位置出现突跃导致严重错误,所以遇到浮点误差的话,我会强制将角度设置为0
if(Math.abs(this.image) < 0.0000001)
{
return this.real > 0 ? 0 : Math.PI;
}else if(Math.abs(this.real) < 0.0000001)
{
return this.image > 0 ? Math.PI * 0.5 : (this.image == 0 ? 0 : - Math.PI * 0.5);
}else
{
return Math.atan2(this.image, this.real);
}
}
/**
* 复数的辐角主值,以角度值表示(跟弧度相比,该方法能更有效地避免边缘位置的浮点误差引发的错误)
*
*/
Object.defineProperty(this, "degree", {get: getDegree});
function getDegree()
{
//由于复数开方基于角度,所以一旦有浮点误差就会导致角度在边缘位置出现突跃导致严重错误,所以遇到浮点误差的话,我会强制将角度设置为0
if(Math.abs(this.image) < 0.0000001)
{
return this.real > 0 ? 0 : 180;
}else if(Math.abs(this.real) < 0.0000001)
{
return this.image > 0 ? 90 : (this.image == 0 ? 0 : 270);
}else
{
return Math.atan2(this.image, this.real) / Math.PI * 180;
}
}
/**
* 复数的模(长度)
* @return
*
*/
Object.defineProperty(this, "length", {get: getLength});
function getLength()
{
return Math.sqrt(this.real * this.real + this.image * this.image);
}
/**
* 返回当前复数的一个副本
* @return
*
*/
function clone()
{
return new ComplexNum(this.real, this.image);
}
this.clone = clone;
function toString()
{
var realStr = String((this.real != 0 || this.image == 0) ? real : "");
var imageStr = (this.image == 0) ? "" : ((this.image < 0 ? ("-" + (-this.image)) : ((realStr == "" ? "" : "+") + this.image)) + "i");
return realStr + imageStr;
}
this.toString = toString;
}
formulaUtils.js
/**
* 方程求解工具类
* 由于二次或以上的方程涉及复数,因此所有的解都用复数存储
* ref: https://blog.csdn.net/iloveas2014/article/details/83478737
*
*/
function FormulaUtil()
{
}
/**
* 计算方程ax+b=0的解
* 一次更没什么好说的了,小学的东西
* @param a
* @param b
* @return
*
*/
FormulaUtil.calcLineFormulaZero = function(a, b)
{
var results = [];
//最高次项系数为0,方程无解或者有无穷个解,此处忽略
if(a != 0)
{
results.push(new ComplexNum(-b / a));
}
return results;
}
/**
* 计算方程ax^2+bx+c=0的两个解
* 二次没什么好说的了,初中的东西
* @param a
* @param b
* @param c
* @return
*
*/
FormulaUtil.calcSquareFormulaZero = function(a, b, c)
{
//最高次项系数为0,用低一次的方程求解
if(FormulaUtil.near0(a))
{
return FormulaUtil.calcLineFormulaZero(b, c);
}
var results = [];
//二次判别式部分
var deltaRoot = new ComplexNum(b * b - 4 * a * c).squareRoot();
for(var i = 0; i < 2; i ++)
{
results.push(new ComplexNum(-b).add(deltaRoot[i]).divideNumber(2 * a));
}
return results;
}
/**
* 计算方程ax^3+bx^2+cx+d=0的3个解
* 这里用一个我到现在都还没搞懂原理但形式足够简洁的盛金公式法来实现
* @param a 3次项系数
* @param b 2次项系数
* @param c 1次项系数
* @param d 常数项
* @return
*
*/
FormulaUtil.calcCubicFormulaZero = function(a, b, c, d)
{
//最高次项系数为0,用低一次的方程求解
if(FormulaUtil.near0(a))
{
return FormulaUtil.calcSquareFormulaZero(b, c, d);
}
//加入特殊情况处理,目的在于减少不必要的精度损失
//形如ax^3+d=0的情况,直接开方即可
if(FormulaUtil.near0(b) && FormulaUtil.near0(c))
{
return new ComplexNum(-d / a).cubicRoot();
}
//ax^3+bx^2=0,常数项和一次项都为0,两个根为0,然后降为一次即可
if(FormulaUtil.near0(d) && FormulaUtil.near0(c))
{
var lineRoots = FormulaUtil.calcLineFormulaZero(a, b);
lineRoots.unshift(new ComplexNum());
lineRoots.unshift(new ComplexNum());
return lineRoots;
}
//ax^3+bx^2+cx=0,常数项为0,一个根为0,然后降为两次即可
if(FormulaUtil.near0(d))
{
var squareRoots = FormulaUtil.calcSquareFormulaZero(a, b, c);
squareRoots.unshift(new ComplexNum());
return squareRoots;
}
var A = b * b - 3 * a * c;
var B = b * c - 9 * a * d;
var C = c * c - 3 * b * d;
var DELTA = B * B - 4 * A * C;
var i = 0;
var results = [];
var x1;
var x;
console.log(DELTA);
if(A == 0 && B == 0)
{
for(i = 0; i < 3; i ++)
{
results.push(new ComplexNum(-b / 3 / a));
}
}else if(DELTA > 0)
{
//这里本来想偷懒下,用二次方程的公式套进去,但没想到A=0就不能用了
var roots = [];
//二次判别式部分
var deltaRoot = new ComplexNum(B * B - 4 * A * C).squareRoot();
for(i = 0; i < 2; i ++)
{
roots.push(new ComplexNum(-B).add(deltaRoot[i]).divideNumber(2));
}
var ys = [];
//y的立方根
var ycrs = [];
for(i = 0, len = roots.length; i < len; i ++)
{
var root = roots[i];
var y = root.multiplyNumber(a * 3).addNumber(A * b);
ys.push(y);
ycrs.push(new ComplexNum((y.real > 0 ? 1 : -1) * Math.pow(Math.abs(y.real), 1 / 3)));
}
x1 = new ComplexNum(-b).subtract(ycrs[0]).subtract(ycrs[1]).divideNumber(3 * a);
console.log(ycrs[0], ycrs[1]);
results.push(x1);
for(i = 0; i < 2; i ++)
{
x = new ComplexNum(-2 * b).add(ycrs[0]).add(ycrs[1]).
add(ycrs[0].subtract(ycrs[1]).multiply(ComplexConsts.I).
multiplyNumber(i == 0 ? Math.sqrt(3) : -Math.sqrt(3))).divideNumber(6 * a);
results.push(x);
}
}else if(DELTA == 0)
{
var K = B / A;
results.push(new ComplexNum(- b / a + K), - 1 / 2 * K, - 1 / 2 * K);
}else if(DELTA < 0)
{
//盛金公式上说这种情况下A必大于0,所以就没用复数来搞了
var T = (2 * A * b - 3 * a * B) / 2 * Math.sqrt(A * A * A);
var theta = Math.acos(T);
x1 = new ComplexNum((-b - 2 * Math.sqrt(A) * Math.cos(theta / 3)) / 3 / a);
for(i = 0; i < 2; i ++)
{
x = new ComplexNum(-b + Math.sqrt(A) * (Math.cos(theta / 3) + (i == 0 ? 1 : -1) * Math.sin(theta / 3) * Math.sqrt(3)) / 3 / a);
}
}
return results;
}
/**
* 计算方程ax^4+bx^3+cx^2+dx+e=0的4个解
* 以下代码按照费拉里公式进行实现
* @param a 4次项系数
* @param b 3次项系数
* @param c 2次项系数
* @param d 1次项系数
* @param e 常数项
* @return
*
*/
FormulaUtil.calcFourFormulaZero = function(a, b, c, d, e)
{
//最高次项系数为0,用低一次的方程求解
if(FormulaUtil.near0(a))
{
return FormulaUtil.calcCubicFormulaZero(b, c, d, e);
}
//测试发现,费拉里法无法处理一些特殊情况,m=0时出错几率较高,但未能找出必现规律,为此,对于一些能用简单方法直接降次数的情况,此处加入特殊处理
//此外,特殊情况处理的好处是运算量小,可以减少中途计算中的精度损失
//形如ax^4+e=0的情况,直接开方即可
if(FormulaUtil.near0(b) && FormulaUtil.near0(c) && FormulaUtil.near0(d))
{
return new ComplexNum(- e / a).getRoot(4);
}
//ax^4+bx^3=0,常数项,一次项,二次项均为0,则有三个根为0,然后直接降到1次即可
if(FormulaUtil.near0(c) == 0 && FormulaUtil.near0(d) && FormulaUtil.near0(e))
{
var lineRoots = calcLineFormulaZero(a, b);
lineRoots.unshift(new ComplexNum());
lineRoots.unshift(new ComplexNum());
lineRoots.unshift(new ComplexNum());
return lineRoots;
}
//ax^4+bx^3+cx^2=0,常数项和一次项为0,则有两个根为0,然后直接降到2次即可
if(FormulaUtil.near0(d) && FormulaUtil.near0(e))
{
var squareRoots = FormulaUtil.calcSquareFormulaZero(a, b, c);
squareRoots.unshift(new ComplexNum());
squareRoots.unshift(new ComplexNum());
return squareRoots;
}
//ax^4+bx^3+cx^2+dx=0,常数项为0,有一个根为0,然后直接降到3次即可
if(FormulaUtil.near0(e))
{
var cubicRoots = FormulaUtil.calcCubicFormulaZero(a, b, c, d);
cubicRoots.unshift(new ComplexNum());
return cubicRoots;
}
//ax^4+cx^2+e=0,一次项和三次项为0,为双二次方程,用换元法让y=x^2即可降为两次
if(FormulaUtil.near0(b) && FormulaUtil.near0(d))
{
var twoSquareRoots = FormulaUtil.calcSquareFormulaZero(a, c, e);
var fourRoots = twoSquareRoots[0].squareRoot().concat(twoSquareRoots[1].squareRoot());
return fourRoots;
}
var P = (c * c + 12 * a * e - 3 * b * d) / 9;
var Q = (27 * a * d * d + 2 * c * c * c + 27 * b * b * e - 72 * a * c * e - 9 * b * c * d) / 54;
var D = new ComplexNum(Q * Q - P * P * P).squareRoot()[0];
var u1 = new ComplexNum(Q).add(D).cubicRoot()[0];
var u2 = new ComplexNum(Q).subtract(D).cubicRoot()[0];
var u = u1.length > u2.length ? u1 : u2;
var v = (u.real == 0 && u.image == 0) ? new ComplexNum() :(new ComplexNum(P).divide(u));
var omegas = [ComplexConsts.OMEGA_ZERO, ComplexConsts.OMEGA, ComplexConsts.OMEGA_SQUARE, ComplexConsts.OMEGA_CUBIC];
var currentMLength = 0;
var maxM;
var currentOmegaObj;
//算出所有的m来,并取出最大值
for(var k = 0; k < 3; k ++)
{
var m = new ComplexNum(b * b - 8 / 3 * a * c);
var omegaObj = u.clone();//omegas[k].multiply(u);
omegaObj = omegaObj.add(v);
omegaObj = omegaObj.multiplyNumber(4 * a);
m = m.add(omegaObj);
m = m.squareRoot()[0];
if(m.length >= currentMLength)
{
currentOmegaObj = omegaObj;
currentMLength = m.length;
maxM = m;
}
}
m = maxM;
omegaObj = currentOmegaObj;
var S = new ComplexNum(2 * b * b - 16 / 3 * a * c);
S = S.subtract(omegaObj);
var T;
if(!FormulaUtil.near0(m.real) || !FormulaUtil.near0(m.image))
{
T = new ComplexNum(8 * a * b * c - 16 * a * a * d - 2 * b * b * b);
T = T.divide(m);
}else
{
T = new ComplexNum();
}
var results = [];
for(var n = 1; n <= 4; n ++)
{
var value = new ComplexNum();
//-1的[n/2]次方,[n/2]表示小于n/2的最大整数
var minus1Pow0_5 = n > 2 ? -1 : 1;
value = value.subtractNumber(b);
value = value.add((new ComplexNum(minus1Pow0_5, 0).multiply(m)));
value = value.add(S.add(new ComplexNum(minus1Pow0_5, 0).multiply(T)).squareRoot()[0].multiplyNumber(n % 2 == 0 ? -1 : 1));
value = value.divideNumber(4 * a);
results.push(value);
}
return results;
}
/**
* 计算多项式方程的解
* @param args
*
*/
FormulaUtil.calcPolyFormulaZero = function()
{
var currentArgs = arguments.concat();
while(currentArgs.length > 0 && currentArgs[0] == 0)
{
currentArgs.shift();
}
var argCount = currentArgs.length;
if(argCount == 0)
{
throw new Error("必须传入参数");
return null;
}
if(argCount <= 1)
{
return [];
}
if(argCount <= 5)
{
return _polyZeroFunctions_vec[argCount - 1].apply(null, currentArgs);
}
var i, len;
//导数后的系数
//对于5次或以上的情况,可以通过导数降低次数,然后用切线法求出近似值
var dArgs = FormulaUtil.getDArgs(currentArgs);
//二阶导数的系数
var d2Args = FormulaUtil.getDArgs(dArgs);
//先算出导数等于0的点(可能是极值点)
var dSolutions = FormulaUtil.calcPolyFormulaZero.apply(null, dArgs);
//解方程的过程可能会出现虚根,求近似值只能去掉了(暂没想到比较好的求近似虚根的方法)
var dRealSolutions = FormulaUtil.getRealSolutions(dSolutions);
dRealSolutions.sort(Array.NUMERIC);
var yValues = [];
var realSolutions = [];
for(i = 0, len = dRealSolutions.length; i < len; i ++)
{
var solution = dRealSolutions[i];
yValues.push(getPolyValue(solution, currentArgs));
}
//无解的话可能是单调递增或者递减,这时候应该补上一个解,另外,最左侧的零点左侧和最右侧的零点右侧都可能有解,这些逻辑暂时还没做
for(i = 0, len = yValues.length - 1; i < len; i ++)
{
if(yValues[i] * yValues[i + 1] < 0)
{
var xValue = findRoot(dRealSolutions[i], dRealSolutions[i + 1], currentArgs, dArgs, d2Args);
console.log("在" + dRealSolutions[i] + "和" + dRealSolutions[i + 1] + "之间有一个解x=" + xValue);
realSolutions.push(new ComplexNum(xValue));
}else if(yValues[i] == 0)
{
realSolutions.push(new ComplexNum(dRealSolutions[i]));
}else if(yValues[i + 1] == 0)
{
realSolutions.push(new ComplexNum(dRealSolutions[i + 1]));
}
}
return realSolutions;
}
FormulaUtil.getPolyValue = function(xValue, args)
{
var argCount = args.length;
var value = 0;
//遍历所有次方的项,然后累加
for(var i = 0, len = argCount; i < len; i ++)
{
var currentK = args[i];
//求出当前项的次数
var times = argCount - 1 - i;
value += currentK * (times == 0 ? 1 : Math.pow(xValue, times));
}
return value;
}
/**
* 在指定区间内找到一个高次方程的解
* @param min 区间的下限
* @param max 区间的上限
* @param formulaArgs 高次方程的系数
* @param dArgs 方程一阶导数的系数
* @param d2Args 方程二阶导数的系数
* @param precision 允许的最大误差
* @return
*
*/
FormulaUtil.findRoot = function(min, max, formulaArgs, dArgs, d2Args, precision)
{
if(isNaN(precision))
{
precision = 0.00001;
}
//最好用牛顿切线法,但现在先用二分法凑合一下吧
do
{
var center = (min + max) / 2;
var minYValue = getPolyValue(min, formulaArgs);
var maxYValue = getPolyValue(max, formulaArgs);
var centerYValue = getPolyValue(center, formulaArgs);
if(centerYValue == 0)
{
return center;
}
if(centerYValue * minYValue < 0)
{
max = center;
}else
{
min = center;
}
}while(Math.abs(min - max) >= precision);
return center;
}
FormulaUtil.getDArgs = function(sourceArgs)
{
var dArgs = [];
var argCount = sourceArgs.length;
for(var i = 0, len = argCount - 1; i < len; i ++)
{
var newK = (argCount - 1 - i);
var finalK = newK * sourceArgs[i];
dArgs.push(finalK);
}
return dArgs;
}
/**
* 为了实用上的方便,这里提供一个通过复数解得到实数解的方法,可能有相等的实根
* @param complexNums
* @param tolerance
* @return
*
*/
FormulaUtil.getRealSolutions = function(complexNums, tolerance)
{
if(isNaN(tolerance))
{
tolerance = 0.00001;
}
var numbers = [];
for(var i = 0, len = complexNums.length; i < len; i ++)
{
var item = complexNums[i];
if(FormulaUtil.near0(item.image, tolerance))
{
numbers.push(item.real);
}
}
return numbers;
}
FormulaUtil.near0 = function(num, tolerance)
{
if(isNaN(tolerance))
{
tolerance = 0.0000001;
}
return Math.abs(num) <= tolerance;
}
angleUtils.js
/**
* r
*
*/
function AngleUtil()
{
}
AngleUtil.getCosDic = function()
{
if(AngleUtil._cosDic == undefined)
{
AngleUtil._cosDic = [];
AngleUtil._cosDic[60] = AngleUtil._cosDic[-60] = AngleUtil._cosDic[300] = AngleUtil._cosDic[-300] = 0.5;
AngleUtil._cosDic[120] = AngleUtil._cosDic[-120] = AngleUtil._cosDic[240] = AngleUtil._cosDic[-240] = -0.5;
AngleUtil._cosDic[0] = AngleUtil._cosDic[360] = 1;
AngleUtil._cosDic[180] = AngleUtil._cosDic[-180] = -1;
AngleUtil._cosDic[90] = AngleUtil._cosDic[270] = AngleUtil._cosDic[-90] = AngleUtil._cosDic[-270] = 0;
}
return AngleUtil._cosDic;
}
AngleUtil.getSinDic = function()
{
if(AngleUtil._sinDic == undefined)
{
AngleUtil._sinDic = [];
AngleUtil._sinDic[30] = AngleUtil._sinDic[150] = AngleUtil._sinDic[-330] = AngleUtil._sinDic[-210] = 0.5;
AngleUtil._sinDic[-30] = AngleUtil._sinDic[-150] = AngleUtil._sinDic[210] = AngleUtil._sinDic[330] = -0.5;
AngleUtil._sinDic[90] = AngleUtil._sinDic[-270] = 1;
AngleUtil._sinDic[270] = AngleUtil._sinDic[-90] = -1;
AngleUtil._sinDic[180] = AngleUtil._sinDic[-180] = AngleUtil._sinDic[0] = AngleUtil._sinDic[360] = 0;
}
return AngleUtil._sinDic;
}
AngleUtil.getTanDeg = function(tan) {
var result = Math.atan(tan) / (Math.PI / 180);
return result;
}
AngleUtil.getSinDeg = function(sin) {
var result = Math.asin(sin) * 180 / Math.PI;
return result;
}
AngleUtil.getCosDeg = function(cos) {
var result = Math.acos(cos) * 180 / Math.PI;
return result;
}
参考 https://blog.csdn.net/iloveas2014/article/details/83478737