OpenCV —— 几何形状的检测和拟合(凸包、霍夫直线检测、霍夫圆检测、轮廓)
几何形状的检测和拟合
-
- 点集的最小外包
-
- 最小外包矩形
- 最小外包圆
- 最小外包三角形
- 最小凸包
- 霍夫直线检测
- 霍夫圆检测
-
- 标准霍夫圆检测
- 基于梯度的霍夫圆检测
- 轮廓
-
- 查找、绘制轮廓
- 外包、拟合轮廓
- 轮廓的周长和面积
- 点和轮廓的关系
- 轮廓的凸包缺陷
根据阈值分割和边缘检测可以基本确定物体的边缘或者前景,接下来需要拟合这些边缘和前景,如确定物体边缘是否满足某种几何形状,如直线、圆、椭圆等,或者拟合出包含前景或者边缘像素点的最小外包矩形、圆、凸包等几何形状,为计算它们的面积或者为模板匹配等操作打下坚实的基础。
点集的最小外包
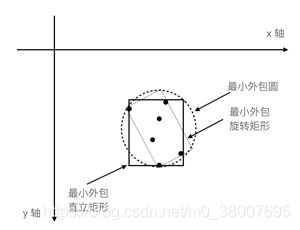
点集是指坐标点的集。已知二维笛卡尔坐标系中的很多坐标点,需要找到包围这些坐标点的最小外包四边形或者圆,在这里最小指的是最小面积,如下图:
最小外包矩形
OpenCV提供了两个关于矩形的类:一个是关于直立矩形的 Rect;另一个是关于旋转矩形的 RotatedRect。只需要三个要素就可以确定一个旋转矩形,它们是中心坐标尺寸(宽、高)和旋转角度。对于 RotatedRect ,OpenCV并没有提供类似于画直立矩形的函数 rectangle ,可以通过画四条边的方式画出该旋转矩形。
首先介绍一下 Rect和 RotateRect 这两个类,都有什么属性和方法:
Point 的主要属性有 x,y
Size 的主要属性有 width,height
template<typename _Tp> class Rect_
{
public:
typedef _Tp value_type;
//! 默认的构造函数
Rect_();
Rect_(_Tp _x, _Tp _y, _Tp _width, _Tp _height);
Rect_(const Rect_& r);
Rect_(Rect_&& r) CV_NOEXCEPT;
Rect_(const Point_<_Tp>& org, const Size_<_Tp>& sz);
Rect_(const Point_<_Tp>& pt1, const Point_<_Tp>& pt2);
Rect_& operator = ( const Rect_& r );
Rect_& operator = ( Rect_&& r ) CV_NOEXCEPT;
//! 左上角顶点
Point_<_Tp> tl() const;
//! 右下角顶点
Point_<_Tp> br() const;
//! 矩形的大小 (width, height)
Size_<_Tp> size() const;
//! 矩形的面积 (width*height)
_Tp area() const;
//! 判断是否为空
bool empty() const;
//! 转换为另一种数据类型
template<typename _Tp2> operator Rect_<_Tp2>() const;
//! 检查矩形是否包含点
bool contains(const Point_<_Tp>& pt) const;
_Tp x; // 左上角的 x 坐标
_Tp y; // 左上角的 y 坐标
_Tp width; // 矩形的宽
_Tp height; //矩形的高
};
class CV_EXPORTS RotatedRect
{
public:
//! 默认的构造函数
RotatedRect();
/** 完整的构造函数
@param center 矩形质心.
@param size 矩形的宽高.
@param angle 顺时针方向的旋转角度。 当角度为0、90、180、270等时,矩形变为直立矩形
*/
RotatedRect(const Point2f& center, const Size2f& size, float angle);
/**
RotatedRect的任意3个顶点。 必须按顺序(顺时针或逆时针)给出。
*/
RotatedRect(const Point2f& point1, const Point2f& point2, const Point2f& point3);
/** 返回矩形的4个顶点
@param pts 用于存储矩形顶点的points数组。 顺序为bottomLeft,topLeft,topRight,bottomRight。
*/
void points(Point2f pts[]) const;
//! 返回包含旋转后的矩形的最小正整数
Rect boundingRect() const;
//! 返回包含旋转矩形的最小(精确)浮点矩形,不适用于图像
Rect_<float> boundingRect2f() const;
//! 返回矩形质心
Point2f center;
//! 返回矩形的宽度和高度
Size2f size;
//! 返回旋转角度。 当角度为0、90、180、270等时,该矩形变为直立矩形。
float angle;
};
接下来介绍两个函数:
RotatedRect minAreaRect(points)根据坐标点得到最小外包旋转矩形Rect boundingRect(points) 根据坐标点得到最小外包直立矩形
minAreaRect
RotatedRect cv::minAreaRect(InputArray points)
//Python:
retval = cv.minAreaRect(points)
输入一个点集,返回一个最小外包旋转矩形
boundingRect
Rect cv::boundingRect(InputArray points)
//Python:
retval = cv.boundingRect(points)
输入一个点集,返回一个最小外包直立矩形
点集可以用以下两种形式来表示:
//形式1
vector<Point2f> points;
points.push_back(Point2f(1, 1));
points.push_back(Point2f(5, 1));
points.push_back(Point2f(1, 10));
points.push_back(Point2f(5, 10));
points.push_back(Point2f(2, 5));
//形式2
Mat points = (Mat_<float>(5, 2) << 1, 1, 5, 1, 1, 10, 5, 10, 2, 5);
再介绍一个函数:
void boxPoints(RotatedRectRect box, OutputArray points) 计算出旋转矩形的四个顶点。也可以使用 RotatedRect::points 方法得到旋转矩形的四个顶点。可以使用这四个顶点画出矩形。
boxPoints
void cv::boxPoints(RotatedRect box,
OutputArray points
)
//Python:
points = cv.boxPoints(box[, points])
C++ 示例
int main()
{
// 点集形式1
// Mat points = (Mat_(5, 2) << 1, 1, 5, 1, 1, 10, 5, 10, 2, 5);
//点集形式2
vector<Point2f> points;
points.push_back(Point2f(1, 1));
points.push_back(Point2f(5, 1));
points.push_back(Point2f(1, 10));
points.push_back(Point2f(5, 10));
points.push_back(Point2f(2, 5));
// 计算点集的最小外包旋转矩形
RotatedRect rRect = minAreaRect(points);
Rect rect = boundingRect(points);
Point2f verticles1[4];
rRect.points(verticles1);
Mat verticles2;
boxPoints(rRect, verticles2);
// 打印旋转矩形的信息
cout << "旋转矩形的角度:" << rRect.angle << endl;
cout << "旋转矩形的中心:" << rRect.center << endl;
cout << "旋转矩形的尺寸:" << rRect.size << endl;
cout << "=================" << endl;
cout << "直立矩形:" << rect << endl;
cout << "直立矩形的左上角x:" << rect.x << endl;
cout << "直立矩形的左上角y:" << rect.y << endl;
cout << "直立矩形的宽:" << rect.width << endl;
cout << "直立矩形的高:" << rect.height << endl;
cout << "=================" << endl;
for(int i = 0; i < 4; i++)
{
cout << verticles1[i].x << "," << verticles1[i].y << endl;
}
cout << verticles2 << endl;
return 0;
}
输出结果
旋转矩形的角度:-90
旋转矩形的中心:[3, 5.5]
旋转矩形的尺寸:[9 x 4]
=================
直立矩形:[5 x 10 from (1, 1)]
直立矩形的左上角x:1
直立矩形的左上角y:1
直立矩形的宽:5
直立矩形的高:10
=================
5,10
1,10
1,1
5,1
[5, 10;
1, 10;
1, 1;
5, 1]
Program ended with exit code: 0
最小外包圆
minEnclosingCircle
void cv::minEnclosingCircle(InputArray points,
Point2f& center,
float& radius
)
//Python:
center, radius = cv.minEnclosingCircle(points)
C++示例
int main()
{
vector<Point2f> points;
points.push_back(Point2f(1, 1));
points.push_back(Point2f(5, 1));
points.push_back(Point2f(1, 10));
points.push_back(Point2f(5, 10));
points.push_back(Point2f(2, 5));
// 计算点集的最小外包圆
Point2f center;
float radius;
minEnclosingCircle(points, center, radius);
cout << center << endl;
cout << radius << endl;
return 0;
}
输出结果
[3, 5.5]
4.92453
最小外包三角形
minEnclosingTriangle
查找包含2D点集的最小面积的三角形,并返回其面积。
该函数找到包围给定2D点集的最小面积的三角形,并返回其面积。
double cv::minEnclosingTriangle(InputArray points,
OutputArray triangle
)
//Python:
retval, triangle = cv.minEnclosingTriangle(points[, triangle])
C++ 示例
int main()
{
vector<Point2f> points;
points.push_back(Point2f(1, 1));
points.push_back(Point2f(5, 1));
points.push_back(Point2f(1, 10));
points.push_back(Point2f(5, 10));
points.push_back(Point2f(2, 5));
// 点集的最小外包三角形
vector<Point> triangle;
double area = minEnclosingTriangle(points, triangle);
cout << "三角形的三个顶点" << endl;
for(int i = 0; i < 3; i++)
{
cout << triangle[i].x << ", " << triangle[i].y << endl;
}
cout << "三角形的面积:" << area << endl;
return 0;
}
输出结果
三角形的三个顶点
9, 1
1, 1
1, 19
三角形的面积:72
最小凸包
给定二维平面上的点集,凸包就是将最外层的点连接起来构成的图多边形,它能包含点集中的所有点,如下图所示
函数 convexHull
void cv::convexHull(InputArray points,
OutputArray hull,
bool clockwise = false,
bool returnPoints = true
)
//Python:
hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]])
参数
| 参数 | 解释 |
|---|---|
| points | 点集 |
| hull | 构成凸包的点,类型为 vector、vector |
| clockwise | hull中的点是按照顺时针还是逆时针排列的 |
| returnPoints | 值为true时,hull中存储的坐标点,值为false时,存储的是这些坐标点在点集中的索引 |
C++示例
int main()
{
vector<Point2f> points;
points.push_back(Point2f(1, 1));
points.push_back(Point2f(5, 1));
points.push_back(Point2f(1, 10));
points.push_back(Point2f(5, 10));
points.push_back(Point2f(2, 5));
// 求点集的凸包
vector<Point2f> hull;
convexHull(points, hull);
for(int i = 0; i < hull.size(); i++)
{
cout << hull[i] << endl;
}
return 0;
}
输出结果
[5, 10]
[1, 10]
[1, 1]
[5, 1]
示例2
int main()
{
int nums = 80;
// 随机生成80个点
srand((unsigned int)time(NULL));
vector<Point2f> points;
for(int i = 0; i < nums; i++)
{
Point2f point;
point.x = rand() % 200 + 100;
point.y = rand() % 200 + 100;
points.push_back(point);
}
// 画出这些点
Mat img = Mat::zeros(400, 400, CV_8UC1);
for(int i = 0; i < nums; i++)
{
circle(img, points[i], 2, Scalar(255, 255, 255), -1);
}
// 求点集的凸包
vector<Point2f> hull;
convexHull(points, hull);
// 连接凸包的点
for(int i = 0; i < hull.size()-1; i++)
{
line(img, hull[i], hull[i+1], Scalar(255, 255, 255), 1);
}
line(img, hull[hull.size()-1], hull[0], Scalar(255, 255, 255), 1);
imwrite("最小凸包.jpg", img);
return 0;
}
霍夫直线检测
原理详解
在 xoy 平面内的一条直线大致分为如下图所示的四种情况:
其中 φ \varphi φ 是直线的正切角, b b b 是直线的截距, o N oN oN 是原点 o o o 到直线的垂线, ρ \rho ρ 是原点到直线的代数距离。当垂线 o N oN oN 在第一象限和第二象限时,令 ρ = ∣ o N ∣ \rho = |oN| ρ=∣oN∣, θ \theta θ 是 o N → \overrightarrow{oN} oN 与 x 轴的正方向的夹角;当垂线 o N oN oN 在第三象限和第四象限时,令 ρ = − ∣ o N ∣ \rho = -|oN| ρ=−∣oN∣ , θ \theta θ 是 o N → \overrightarrow{oN} oN 与 x 轴的负方向的夹角,其中 0 ≤ θ ≤ π 0\leq \theta \leq \pi 0≤θ≤π 。那么直线方程可由 θ \theta θ 和 ρ \rho ρ 表示,即只要用 θ \theta θ 和 ρ \rho ρ 表示出直线的斜率和截距就可以了。
图(a)第一象限: φ = π 2 + θ , b = ρ sin θ \varphi = \frac{\pi}{2} + \theta, b=\frac{\rho}{\sin \theta} φ=2π+θ,b=sinθρ,计算出斜率和截距,则直线方程为 y = tan ( 90 + θ ) x + ρ sin θ = − cos θ sin θ x + ρ sin θ y = \tan(90+\theta)x+\frac{\rho}{\sin \theta} = -\frac{\cos \theta}{\sin \theta}x + \frac{\rho}{\sin \theta} y=tan(90+θ)x+sinθρ=−sinθcosθx+sinθρ,整理后可得 ρ = x cos θ + y sin θ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ。
图(b)第二象限: φ = θ − π 2 , b = ρ sin θ \varphi = \theta - \frac{\pi}{2}, b=\frac{\rho}{\sin \theta} φ=θ−2π,b=sinθρ,计算出斜率和截距,则直线方程为 y = tan ( θ − 90 ) x + ρ sin θ = − cos θ sin θ x + ρ sin θ y = \tan(\theta - 90)x+\frac{\rho}{\sin \theta} = -\frac{\cos \theta}{\sin \theta}x + \frac{\rho}{\sin \theta} y=tan(θ−90)x+sinθρ=−sinθcosθx+sinθρ,整理后可得 ρ = x cos θ + y sin θ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ。
图©第三象限: φ = π 2 + θ , b = ρ sin θ \varphi = \frac{\pi}{2} + \theta, b=\frac{\rho}{\sin \theta} φ=2π+θ,b=sinθρ,计算出斜率和截距,则直线方程为 y = tan ( 90 + θ ) x + ρ sin θ = − cos θ sin θ x + ρ sin θ y = \tan(90+\theta)x+\frac{\rho}{\sin \theta} = -\frac{\cos \theta}{\sin \theta}x + \frac{\rho}{\sin \theta} y=tan(90+θ)x+sinθρ=−sinθcosθx+sinθρ,整理后可得 ρ = x cos θ + y sin θ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ。
图(d)第四象限: φ = θ − π 2 , b = ρ sin θ \varphi = \theta - \frac{\pi}{2}, b=\frac{\rho}{\sin \theta} φ=θ−2π,b=sinθρ,计算出斜率和截距,则直线方程为 y = tan ( θ − 90 ) x + ρ sin θ = − cos θ sin θ x + ρ sin θ y = \tan(\theta - 90)x+\frac{\rho}{\sin \theta} = -\frac{\cos \theta}{\sin \theta}x + \frac{\rho}{\sin \theta} y=tan(θ−90)x+sinθρ=−sinθcosθx+sinθρ,整理后可得 ρ = x cos θ + y sin θ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ。
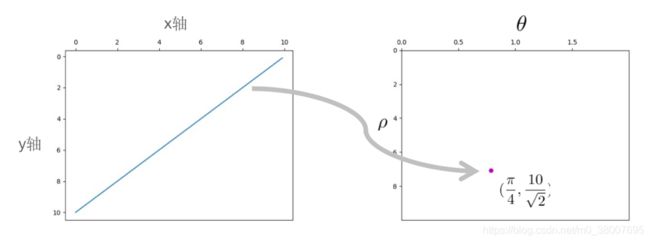
可以发现,计算完成四个象限的直线方程,最后的表示结果是一样的,即如果知道原点到一条直线的代数距离与x轴的夹角,则直线方程可由以下方式表示:
ρ = x cos θ + y sin θ \rho = x \cos \theta + y \sin \theta ρ=xcosθ+ysinθ
当然,反过来也可以,如果知道平面内的一条直线,那么可以计算出唯一的 ρ \rho ρ 和 θ \theta θ ,即 xoy 平面内的任意一条直线对应参数空间(或称霍夫空间) θ o ρ \theta o \rho θoρ 中的一点 ( ρ , θ ) (\rho, \theta) (ρ,θ) 中的一点 ( ρ , θ ) (\rho, \theta) (ρ,θ)。如下图所示,对于 xoy 平面内的直线 y = 10 − x y = 10 - x y=10−x ,因为原点到该直线的垂线在第一象限,垂线与 x 轴正方向的夹角为 π 4 \frac{\pi}{4} 4π ,原点到该直线的代数距离为 10 2 \frac{10}{\sqrt{2}} 210,所以该直线对应到 θ o ρ \theta o \rho θoρ 中的点 ( π 4 , 10 2 ) (\frac{\pi}{4}, \frac{10}{\sqrt{2}}) (4π,210)。
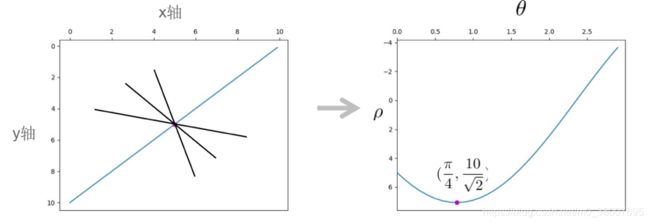
从另一个角度考虑,过 xoy 平面内的一点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 有无数条直线,则对应霍夫空间中的无数个点,这无数个点连接起来就是 θ o ρ \theta o \rho θoρ 平面内的曲线 ρ = x 1 cos θ + y 1 sin θ \rho = x_1 \cos \theta + y_1 \sin \theta ρ=x1cosθ+y1sinθ 。如下图所示,过 xoy 平面内的点 ( 5 , 5 ) (5, 5) (5,5) 又无数条直线,则这个点对应到霍夫空间中的曲线 ρ = 5 cos θ + 5 sin θ \rho = 5 \cos \theta + 5 \sin \theta ρ=5cosθ+5sinθ ,其中因为过 ( 5 , 5 ) (5,5) (5,5) 有一条直线是 y = 10 − x y = 10 -x y=10−x ,则该直线对应坐标点 ( π 4 , 10 2 ) (\frac{\pi}{4}, \frac{10}{\sqrt{2}}) (4π,210) ,所以 ρ = 5 cos θ + 5 sin θ \rho = 5 \cos \theta + 5 \sin \theta ρ=5cosθ+5sinθ 过点 ( π 4 , 10 2 ) (\frac{\pi}{4}, \frac{10}{\sqrt{2}}) (4π,210) 。
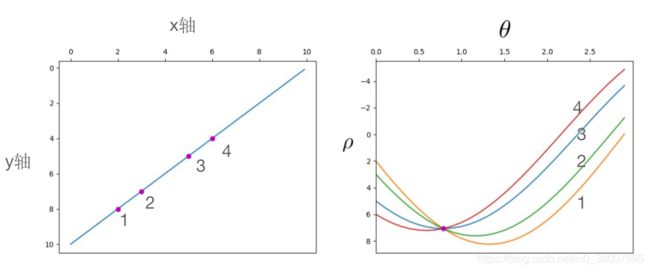
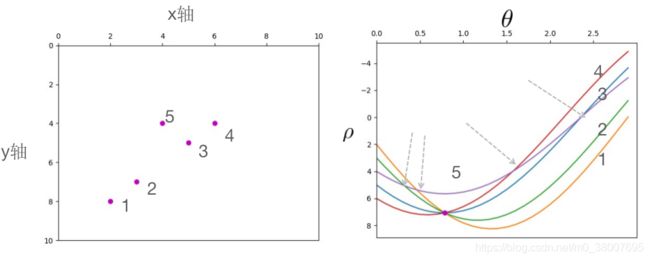
如果要验证 xoy 平面内的 ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . (x_1, y_1), (x_2, y_2)... (x1,y1),(x2,y2)... 是否共线,只需要曲线 ρ = x i cos θ + y i sin θ , i = 1 , 2 , . . . \rho = x_i \cos \theta + y_i \sin \theta, i = 1, 2, ... ρ=xicosθ+yisinθ,i=1,2,... 在 θ o ρ \theta o \rho θoρ 平面内相交与一个点就可以了。例如:在 xoy 平面内有四个点 1、2、3、4.坐标依次为 ( 2 , 8 ) , ( 3 , 7 ) , ( 5 , 5 ) , ( 6 , 4 ) (2,8),(3,7),(5,5), (6,4) (2,8),(3,7),(5,5),(6,4),根据这四个点可以在 θ o ρ \theta o \rho θoρ 平面内画出对应的四条曲线,这四条曲线相交与一个点,所以这四个点是共线的,如下图所示。过这四个点的直线是 y = 10 − x y = 10 -x y=10−x ,所以相交点为 ( π 4 , 10 2 ) (\frac{\pi}{4}, \frac{10}{\sqrt{2}}) (4π,210)。
已知平面内的一些点,要找出哪些点在同一条直线上。例如:xoy 平面内有5个点,对应到 θ o ρ \theta o \rho θoρ 平面内的5条曲线,可以看出1、2、3、4点对应的曲线是相交与一个点的,所以 xoy 平面内的1、2、3、4点是共线的;同样,5点和4点对应的曲线也相交与一个点,所以 xoy 平面内的 5 点和 4 点是共线的;其他的与之类似。
结论:判断 xoy 平面内哪些点是共线的,首先求出每一个点对应到霍夫空间的曲线,然后判断哪几条曲线相交与一点,最后将相交与一点的曲线反过来对应到 xoy 平面内的点,这些点就是共线的,这就是在图像中进行标准霍夫直线检测的核心思想。
C++ 实现
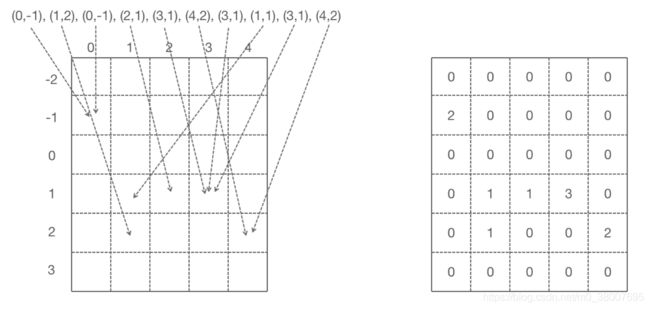
在图像中要解决的霍夫直线检测是针对二值图的,验证哪些前景或者边缘像素点是共线的。在真正程序实现中,因为自变量 0 ≤ θ ≤ 18 0 ∘ 0 \leq \theta \leq 180^{\circ} 0≤θ≤180∘ 有无数个点,所以需要进行离散化处理,每间隔 Δ θ \Delta \theta Δθ 计算一个对应的 ρ \rho ρ , Δ θ \Delta \theta Δθ 通常取 1 ∘ 1^{\circ} 1∘ ,即计算 0 ∘ , 1 ∘ , 2 ∘ , . . . , 17 9 ∘ 0^{\circ},1^{\circ},2^{\circ},...,179^{\circ} 0∘,1∘,2∘,...,179∘ 对应的 ρ \rho ρ 值。当然. Δ θ \Delta \theta Δθ 也可以取和更小的值,但是一般取 1 ∘ 1^{\circ} 1∘ 就够了,所以根据每个白色像素点的坐标就需要计算180个坐标点。然后使用二维直方图(计数器)来验证哪些点是共线的。
例如下图,对其中10个点进行计数,得到计数结果,可知点 (3, 1) 出现了3次,点 (0,-1) 出现了两次。即,相交与 (3,1) 点的直线映射到 xoy 平面内的点共线。
构造霍夫空间中的计数器:假设在 xoy 平面内有任意一点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) ,过该点有无数条直线,但是原点到这些直线的距离不会超过 x 1 2 + y 1 2 \sqrt{x_1^2+y_1^2} x12+y12 。图像矩阵宽度为W,高度为H,设 L = round ( W 2 + H 2 ) + 1 L = \text{round}({\sqrt{W^2+H^2}}) + 1 L=round(W2+H2)+1,那么可以构造计数器 0 ≤ θ ≤ 180 , − L ≤ ρ ≤ L 0 \leq \theta \leq 180, -L \leq \rho \leq L 0≤θ≤180,−L≤ρ≤L 。通过定义函数 HTLine 来实现计数器功能,其中输入 image 是一张二值图,返回值是计数器及对应的哪些点是共线的
map<vector<int>, vector<Point> > HTLine(Mat img, Mat& accumulator, float stepTheta, float stepRho)
{
// 图像的高
int rows = img.rows;
int cols = img.cols;
// 可能出现的最大垂线的长度
int L = round(sqrt(pow(rows-1, 2.0) + pow(cols-1, 2.0))) + 1;
// 初始化计数器
int numtheta = int(180.0 / stepTheta);
int numRho = int(2 * L / stepRho + 1);
accumulator = Mat::zeros(Size(numtheta, numRho), CV_32SC1);
// 初始化 map 类,用于存储共线的点
map<vector<int>,vector<Point> > lines;
for (int i = 0; i < numRho; i++)
{
for( int j = 0; j < numtheta; j++)
{
lines.insert(make_pair(vector<int>(j, i), vector<Point>()));
}
}
// 投票计数
for (int y = 0; y < rows; y++)
{
for (int x = 0; x < cols; x++)
{
if(img.at<uchar>(Point(x, y)) == 255)
{
for(int m = 0; m < numtheta; m++)
{
//对每一个角度,计算对应的rho值
float rho1 = x * cos(stepTheta * m / 180.0 * CV_PI);
float rho2 = y * sin(stepTheta * m / 180.0 * CV_PI);
float rho = rho1 + rho2;
// 计算投票到哪一个区域
int n = int(round(rho + L) / stepRho);
// 累加1
accumulator.at<int>(n, m) += 1;
//记录该点
lines.at(vector<int>(m, n)).push_back(Point(x,y));
}
}
}
}
return lines;
}
直线检测:
int main()
{
string outdir = "./";
// 输入图像
Mat img = imread("/img1.jpg", 0);
// 图像边缘检测
Mat edge;
Canny(img, edge, 50, 200);
imwrite(outdir + "edge.jpg", edge);
//霍夫直线检测
Mat accu;
map<vector<int>, vector<Point> > lines;
lines = HTLine(edge, accu);
// 计数器的灰度级可视化
double maxValue;
minMaxLoc(accu, NULL, &maxValue, NULL, NULL);
//画出计数器大于某一阈值的直线
int vote = 150;
for(int r = 1; r < accu.rows-1; r++)
{
for(int c = 1; c < accu.cols-1; c++)
{
int current = accu.at<int>(r, c);
// 画直线
if(current > vote)
{
int lt = accu.at<int>(r-1, c-1); // 左上
int t = accu.at<int>(r-1, c); // 正上
int rt = accu.at<int>(r-1, c+1); // 右上
int l = accu.at<int>(r, c-1); // 左
int right = accu.at<int>(r, c+1); // 有
int lb = accu.at<int>(r+1, c-1); // 右上
int b = accu.at<int>(r+1, c); // 下
int rb = accu.at<int>(r+1, c+1); // 右下角
// 判断该位置是不是局部最大值
if(current > lt && current > t && current > rt && current > l && current > right && current > lb && current > b && current > rb)
{
vector<Point> line = lines.at(vector<int>(c, r));
int s = line.size();
// 画线
cv::line(img, line.at(0), line.at(s-1), Scalar(255), 2);
}
}
}
}
imwrite(outdir + "lines.jpg", img);
return 0;
}
OpenCV 函数
标准的霍夫直线检测函数 HoughLines
void cv::HoughLines(InputArray image,
OutputArray lines,
double rho,
double theta,
int threshold,
double srn = 0,
double stn = 0,
double min_theta = 0,
double max_theta = CV_PI
)
//Python:
lines = cv.HoughLines(image, rho, theta, threshold[, lines[, srn[, stn[, min_theta[, max_theta]]]]])
标准的霍夫直线检测内存消耗比较大,执行时间比较长,基于这一点,提出了概率霍夫直线检测,它随机地从边缘二值图中选择前景像素点,确定检测直线的两个参数,其本质上还是标准的霍夫直线检测。
概率霍夫直线检测 HoughLinesP
void cv::HoughLinesP(InputArray image,
OutputArray lines,
double rho,
double theta,
int threshold,
double minLineLength = 0,
double maxLineGap = 0
)
//Python:
lines = cv.HoughLinesP(image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]])
| 参数 | 解释 |
|---|---|
| image | 二值图 |
| lines | 线的输出向量。 每条线由一个4元素向量 ( x 1 , y 1 , x 2 , y 2 ) (x_1, y_1, x_2, y_2) (x1,y1,x2,y2) 表示,其中 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 和 ( x 2 , y 2 ) (x_2, y_2) (x2,y2) 是每个检测到的线段的端点。 |
| rho | 累加器的距离分辨率(以像素为单位)。 |
| theta | 累加器的角度分辨率(以弧度为单位)。 |
| threshold | 累加器阈值参数。 仅返回获得足够投票的那些行(> threshold)。 |
| minLineLength | 最小线长。 短于此长度的将被拒绝。 |
| maxLineGap | 连接同一条线上的点之间的最大允许间隙。 |
霍夫圆检测
标准霍夫圆检测
已知圆的圆心坐标是 (a,b),半径为 r,则圆在 xoy 平面内的方程可表示为: ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2 + (y-b)^2 = r^2 (x−a)2+(y−b)2=r2。反过来考虑一个简单的问题:已知 xoy 平面内的点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . (x_1, y_1), (x_2, y_2), (x_3, y_3), ... (x1,y1),(x2,y2),(x3,y3),... ,且知道这些点在一个半径为 r 的圆上,如何求这个圆的圆心。下面通过一个简单的示例来理解这个问题的求解过程。
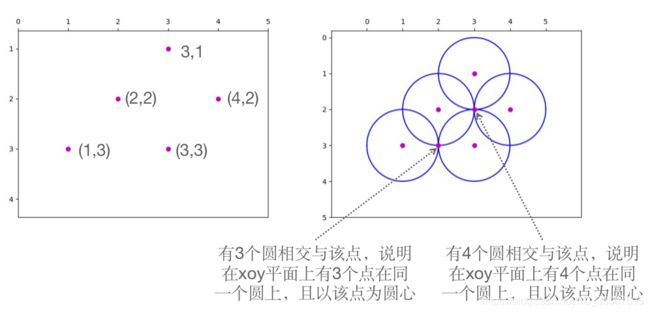
假设在 xoy 平面内有三个点 ( 1 , 3 ) , ( 2 , 2 ) , ( 3 , 3 ) (1,3), (2,2), (3,3) (1,3),(2,2),(3,3) ,且知道这三个点在一个半径为 1 的圆上,通过尺规作图法可以找到圆心,以每个点为圆心、1为半径分别做圆。将 (1,3) 带入圆的方程中的 ( a − 1 ) 2 + ( b − 3 ) 2 = 1 2 (a-1)^2 + (b-3)^2 = 1^2 (a−1)2+(b−3)2=12 ,所以可以理解为一个点对应到 aob 平面内的一个圆;同理,通过其他两个点也可以得到两个圆,那么这三个圆在 aob 平面内共同的焦点,即为三个点共圆的圆心。
在上面问题的基础上,提出一个稍微复杂一点的问题:已知 xoy 平面内的点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . (x_1, y_1), (x_2,y_2), (x_3, y_3),... (x1,y1),(x2,y2),(x3,y3),... 且已知这些点在多个圆上,并且这些圆的半径均为 r,那么哪些点在同一个圆上,并计算出圆心的坐标。
举例:已知在 xoy 平面内有 5 个点 ( 1 , 3 ) , ( 2 , 2 ) , ( 3 , 3 ) , ( 3 , 1 ) , ( 4 , 3 ) (1,3), (2,2), (3,3),(3,1), (4, 3) (1,3),(2,2),(3,3),(3,1),(4,3) 且知道这些点可能位于不同的圆上,这些圆的半径均为1,求出哪些点在同一个圆上,这里也用尺规作图法,首先分别以 5 个点为圆心、1为半径做出5个圆,圆的交点即为圆心,
以上两种情况均是在已知半径的情况下,现在引入一个更复杂的问题:已知 xoy 平面内的点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . (x_1, y_1), (x_2,y_2), (x_3, y_3),... (x1,y1),(x2,y2),(x3,y3),... 求出哪些点在同一个圆上且半径是多少,以及圆心的坐标。因为多了一个参数,所以需要第三维的坐标r,即需要在三维空间 abr 中讨论该问题。任意一个点 ( x i , y i ) (x_i, y_i) (xi,yi) 对应到 abr 空间中的锥面 r 2 = ( a − x i ) 2 + ( b − y i ) 2 r^2 = (a-x_i)^2+(b-y_i)^2 r2=(a−xi)2+(b−yi)2 ,那么如果多个锥面相交与一点 ( a ′ , b ′ , r ′ ) (a',b',r') (a′,b′,r′) ,则说明这些锥面对应的 xoy 平面内的点是共圆的且圆心为 ( a ′ , b ′ ) (a',b') (a′,b′) ,半径为 r ′ r' r′。
该过程相当于先固定 r,然后转换为以上讨论的已知 r 的情况,即第二个问题是第三个问题的一种特殊情况,
与霍夫直线检测类似,图像的霍夫圆检测就是检测哪些前景或边缘像素点在同一个圆上,并给出对应圆的圆心坐标及圆的半径;而且仍然需要计数器来完成该过程,只是这里的计数器从二维变成了三维。
尽管标准的霍夫变换对于曲线检测是一项强有力的技术,但是随着曲线参数数目的增加,造成计数器的数据结构越来越复杂,如直线检测计数器是二维的,圆检测计数器是三维的,这需要大量的存储空间和巨大的计算量,因此采用其他方法进行改进,如同概率直线检测对标准霍夫直线检测的改进,那么基于梯度的霍夫圆检测就是对标准霍夫圆检测的改进。
基于梯度的霍夫圆检测
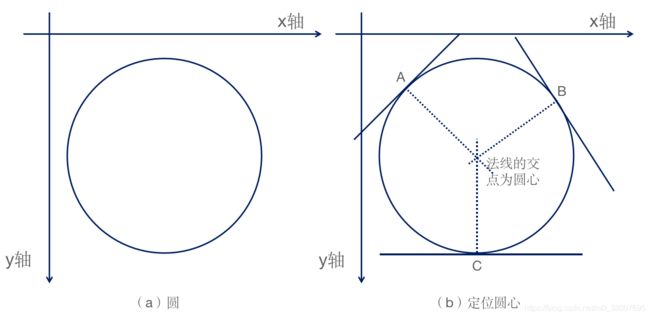
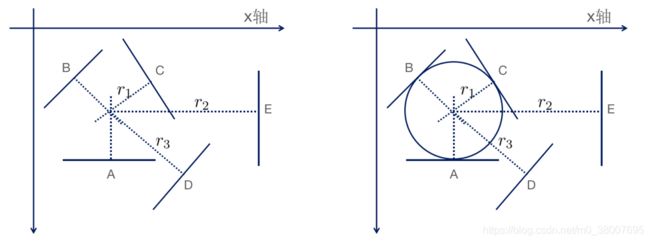
首先提出一个问题:如下图所示,如何通过尺规作图法找到圆的圆心,并量出半径。首先在圆上至少找到两个点,如下图所示,取三个点A、B、C,然后画出经过A、B、C的圆的切线,再分别经过这三个点作切线的垂线(法线),那么这三条法线的交点就是圆心,从圆心到圆上任意一点的距离即为圆的半径。
现在反过来考虑一个问题:假设已知某些点,并知道这些点的梯度方向(切线方向),那么如何定位哪些点在同一个圆上,并计算出对应圆的半径。假设已知 xoy 平面内的点 A、B、C、D、E,且知道这些点的梯度方向,首先画出过这些点的法线,那么交点就有可能是圆心,注意只是有可能,还需要通过下一步量半径的过程,进一步确定哪些交点是圆心。假设交点 O 到 A、B、C这三个点的距离是 r 1 r_1 r1,到D点的距离是 r 3 r_3 r3,到E点的距离是 r 2 r_2 r2,也就是 5 个点到交点 O 半径为 r 1 r_1 r1 的支持度是1,半径为 r 3 r_3 r3 的支持度是1,通过支持度的高低作为最后对圆的选择,如下图:
基于梯度的霍夫圆检测的答题步骤是,首先定位圆心(两个参数),然后计算半径(一个参数)。在代码实现中,首先构造一个二维计数器,然后再构造一个一维计数器,所以又称2-1霍夫圆检测。
Open CV提供的函数 HoughCircles 实现了基于梯度的霍夫圆检测,在该函数的实现过程中,使用了 Sobel 算子且内部实现了边缘的二值图,所以输入的图像不用像 HoughLinesP 和 HoughLines 一样必须是二值图。
OpenCV 函数
HoughCircles函数
void cv::HoughCircles(InputArray image,
OutputArray circles,
int method,
double dp,
double minDist,
double param1 = 100,
double param2 = 100,
int minRadius = 0,
int maxRadius = 0
)
//Python:
circles = cv.HoughCircles(image, method, dp, minDist[, circles[, param1[, param2[, minRadius[, maxRadius]]]]])
| 参数 | 解释 |
|---|---|
| image | 输入图像矩阵 |
| circles | 返回圆的信息,类型为 vector,每一个 Vec3f 都代表 (x, y, radius),即圆心的位置以及圆的半径 |
| method | 方法,目前只有 HOUGH_GRADIENT,即 2-1 霍夫圆检测 |
| dp | 计数器分辨率与图像分辨率的反比。 例如,如果dp = 1,则累加器具有与输入图像相同的分辨率。 如果dp = 2,则累加器的宽度和高度是其一半。 |
| minDist | 圆心之间的最小距离,如果距离太小,则会产生很多相交的圆;如果距离太大,则会漏掉正确的圆 |
| param1 | Canny 边缘检测的双阈值中的高阈值,低阈值默认是它的一般 |
| param2 | 最小投票数(基于圆心的投票数) |
| minRadius | 需要检测圆的最小半径 |
| maxRadius | 需要检测圆的最大半径 |
C++ 示例
int main()
{
string outdir = "./images/";
// 输入图像
Mat img = imread("硬币.jpg");
Mat gray;
cvtColor(img, gray, COLOR_BGR2GRAY);
vector<Vec3f> circles;
HoughCircles(gray, circles, HOUGH_GRADIENT, 1, 200, 200, 60, 50, 300);
for(int i = 0; i < circles.size(); i++)
{
Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
int radius = circles[i][2];
// 画圆心
circle(img, center, 3, Scalar(0, 0, 255), -1);
// 画圆
circle(img, center, radius, Scalar(0, 0, 255), 2);
}
imwrite(outdir + "hough_circle.jpg", img);
}
轮廓
查找、绘制轮廓
一个轮廓代表一系列的点(像素),这一系列的点构成一个有序的点集,所以可以把轮廓理解为一个有序的点集。在边缘检测、阈值分割中,通过不同的算法得到了边缘二值图或者前景二值图,二值图的背景像素或者前景像素就可以被看成是由多个轮廓(点集)组成的。
函数 findContours 可以将二值图的边缘像素或者前景像素拆分成多个轮廓,便于分开讨论每一个轮廓。
void cv::findContours(InputArray image,
OutputArrayOfArrays contours,
OutputArray hierarchy,
int mode,
int method,
Point offset = Point()
)
//Python:
contours, hierarchy = cv.findContours(image, mode, method[, contours[, hierarchy[, offset]]])
| 参数 | 解释 |
|---|---|
| image | 二值图像 |
| contours | 检测到的轮廓。 每个轮廓都存储为点的向量(例如std :: vector |
| hierarchy | 可选的输出向量(例如std :: vector < cv :: Vec4i>),包含有关图像拓扑的信息。 它具有与轮廓数量一样多的元素。 对于每个第i个轮廓 contours[i],hierarchy[i] [0],hierarchy[i] [1],hierarchy[i] [2]和hierarchy[i] [3] 分别表示为在同一层次级别下一个和上一个轮廓的轮廓中的索引、第一个子轮廓和父轮廓。 如果对于轮廓 i,没有下一个,上一个,父级或嵌套的轮廓,则hierarchy[i] 的相应元素将为负数。 |
| mode | 轮廓检索模式 |
| method | 轮廓近似法 |
| offset | 每个轮廓点移动的可选偏移量。 对于从图像ROI中提取轮廓,然后在整个图像上下文中对其进行分析非常有用。 |
参数 mode
-
RETR_EXTERNAL
仅检索外部轮廓。 所有轮廓的 hierarchy[i] [2] = hierarchy [i] [3] =-1。
-
RETR_LIST
在不建立任何层次关系的情况下检索所有轮廓。
-
RETR_CCOMP
检索所有轮廓并将其组织为两级层次结构。 在顶层,组件具有外部边界。 在第二层,有孔的边界。 如果所连接组件的孔内还有其他轮廓,则仍将其放在顶层。
-
RETR_TREE
检索所有轮廓,并重建嵌套轮廓的完整层次。
-
RETR_FLOODFILL
参数 method
-
CHAIN_APPROX_NONE
绝对存储所有轮廓点。 也就是说,轮廓的任意两个后续点(x1,y1)和(x2,y2)将是水平,垂直或对角线邻居,即 max(abs(x1-x2), abs(y2-y1)) == 1。
-
CHAIN_APPROX_SIMPLE
压缩水平,垂直和对角线段,仅保留其端点。 例如,一个直立的矩形轮廓由4个点组成。
-
CHAIN_APPROX_TC89_L1
Teh-Chin链近似算法的一种风格
-
CHAIN_APPROX_TC89_KCOS
Teh-Chin链近似算法的一种风格
函数 drawContours 可以绘制出 findContours 找到的多个轮廓。
void cv::drawContours(InputOutputArray image,
InputArrayOfArrays contours,
int contourIdx,
const Scalar & color,
int thickness = 1,
int lineType = LINE_8,
InputArray hierarchy = noArray(),
int maxLevel = INT_MAX,
Point offset = Point()
)
//Python:
image = cv.drawContours(image, contours, contourIdx, color[, thickness[, lineType[, hierarchy[, maxLevel[, offset]]]]])
| 参数 | 解释 |
|---|---|
| image | 图像矩阵 |
| contours | 所有输入轮廓。 每个轮廓都存储为点向量。 |
| contourIdx | 指示要绘制轮廓的索引。 如果为负,则绘制所有轮廓。 |
| color | 轮廓的颜色 |
| thickness | 轮廓的粗细,负数则填充轮廓区域 |
| lineType | 线型 |
| hierarchy | 有关层次结构的可选信息。 仅当只想绘制一些轮廓时才需要(请参见maxLevel)。 |
| maxLevel | 绘制轮廓的最大等级。 如果为0,则仅绘制指定的轮廓。 如果为1,该函数将绘制轮廓和所有嵌套轮廓。 如果为2,该函数将绘制轮廓,所有嵌套轮廓,所有嵌套至嵌套的轮廓,等等。 仅当存在可用的层次结构时,才考虑此参数。 |
| offset | 可选的轮廓偏移参数。 将所有绘制的轮廓按指定的 offset = ( d x , d y ) \text{offset} = (dx, dy) offset=(dx,dy) 移动 |
C++示例
int main()
{
string outdir = "./images/";
// 输入图像
Mat img = imread("img3.jpg", 0);
// 边缘检测或阈值处理生成一张二值图
Mat gaussImg;
Mat binaryImg;
GaussianBlur(img, gaussImg, Size(3,3), 0.5);
Canny(gaussImg, binaryImg, 50, 200);
imwrite(outdir+"canny.jpg", binaryImg);
// 边缘的轮廓
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(binaryImg, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
for(int i = 0; i < contours.size(); i++)
{
Mat tmp = Mat::zeros(img.rows, img.cols, CV_8UC1);
drawContours(tmp, contours, i, Scalar(255), 2);
imwrite(outdir+to_string(i)+".jpg", tmp);
}
}
接下来,就可以利用所得到的这些轮廓(点集)信息,对最小外包圆、旋转矩形等其他形状进行操作了。
外包、拟合轮廓
介绍了寻找图像中轮廓的方法和点集的拟合,这两部分结合起来,就可以处理目标的定位问题了,如定位上图中的仪表区域。对于定位问题步骤如下:
- 对图像边缘检测或者阈值分割得到二值图,有时也需要对这些二值图进行形态学处理。
- 利用函数
findContours寻找二值图中的多个轮廓。 - 对于通过第二步得到的多个轮廓,其中每一个轮廓都可以作为函数
convexHull、minAreaRect等的参数,然后就可以拟合出包含这个轮廓的最小凸包、最小旋转矩形等。
int main()
{
string outdir = "./images/";
// 输入图像
Mat img = imread("/img3.jpg", 0);
// 边缘检测或阈值处理生成一张二值图
Mat gaussImg;
Mat binaryImg;
GaussianBlur(img, gaussImg, Size(3,3), 0.5);
Canny(gaussImg, binaryImg, 50, 200);
// 边缘的轮廓
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(binaryImg, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
for(int i = 0; i < contours.size(); i++)
{
Rect rect = boundingRect(contours[i]);
// rectangle(img, rect, Scalar(255), 2);
if(rect.area() > 10000) // 筛选出面积大于10000的矩形
{
// 在原图中画出外包矩形
rectangle(img, rect, Scalar(255), 2);
}
}
imwrite(outdir+"仪表检测.jpg", img);
}
假设要定位下图中小狗的区域,仍采用上述方法,首先进行 Canny 边缘检测,然后寻找轮廓,再对每一个轮廓求出最小外包直立矩形,最后对外包矩形进行筛选,只留下面积大于2000的矩形,发现并没有得到我们想要的结果,这是因为下图的边缘信息比较复杂,无法单独得到小狗的边缘,所以这时需要利用另一种常用的二值图,即阈值二值图,不再是边缘二值图。
通过观察,小狗区域的灰度值明显比背景区域大,所以使用阈值处理得到二值图,然后利用该二值图进行寻找轮廓的操作,再进行轮廓的最小外包处理会比较好。
int main()
{
string outdir = "./images/";
// 输入图像
Mat img = imread("img7.jpg", 0);
// 边缘检测或阈值处理生成一张二值图
Mat gaussImg;
Mat binaryImg;
GaussianBlur(img, gaussImg, Size(3,3), 0.5);
threshold(gaussImg, binaryImg, 0, 255, THRESH_OTSU);
Mat kernel = getStructuringElement(MORPH_RECT, Size(5,5));
//形态学开运算(消除细小白点)
morphologyEx(binaryImg, binaryImg, MORPH_OPEN, kernel);
imwrite(outdir+"canny.jpg", binaryImg);
// 边缘的轮廓
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(binaryImg, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
Mat contourImg = Mat::zeros(img.rows, img.cols, CV_8UC1);
for(int i = 0; i < contours.size(); i++)
{
drawContours(contourImg, contours, i, Scalar(255), 2);
// 画出轮廓的最小外包圆
// Point2f center;
// float radius;
// minEnclosingCircle(contours[i], center, radius);
// circle(img, center, radius, Scalar(255), 2);
// 多边形逼近
vector<Point> approxCurve;
approxPolyDP(contours[i], approxCurve, 0.3, true);
for(int i = 0; i < approxCurve.size()-2; i++)
{
line(img, approxCurve[i], approxCurve[i+1], Scalar(0), 2);
}
line(img, approxCurve[approxCurve.size()-1], approxCurve[0], Scalar(0), 2);
}
imwrite(outdir+"小狗.jpg", img);
imwrite(outdir+"小狗轮廓.jpg", contourImg);
}
除了拟合多边形函数 approxPolyDP,OpenCV还提供了 fitline 或者 fitEllipse分别用于拟合直线或者椭圆,背后的原理就是最小二乘法拟合。
void cv::approxPolyDP(InputArray curve,
OutputArray approxCurve,
double epsilon,
bool closed
)
//Python:
approxCurve = cv.approxPolyDP(curve, epsilon, closed[, approxCurve]
| 参数 | 解释 |
|---|---|
| curve | 曲线点集 vector 或者 Mat |
| approxCurve | 近似结果。 类型应与输入曲线的类型匹配。 |
| epsilon | 指定近似精度的参数。 原始曲线与其近似值之间的最大距离。 |
| closed | 如果为true,则近似曲线是闭合的(其第一个和最后一个顶点已连接)。 否则,不闭合。 |
void cv::fitLine(InputArray points,
OutputArray line,
int distType,
double param,
double reps,
double aeps
)
//Python:
line = cv.fitLine(points, distType, param, reps, aeps[, line])
函数 fitline 通过最小化 ∑ i ρ ( r i ) \sum_i \rho(r_i) ∑iρ(ri) 拟合一条线,其中 r i r_i ri 是第 i 个点和线之间的距离, ρ ( r ) \rho(r) ρ(r) 是距离函数
| 参数 | 解释 |
|---|---|
| points | 2D 或 3D 点集 vector 或者 Mat |
| line | 输出直线参数。 如果是2D拟合,则它应该是4个元素的向量(如Vec4f)-(vx,vy,x0,y0),其中(vx,vy)是与线共线的归一化向量,而(x0,y0)是 线上的一点。 如果是3D拟合,则它应该是6个元素的向量(如Vec6f)-(vx,vy,vz,x0,y0,z0),其中(vx,vy,vz)是与线共线的归一化向量,并且 (x0,y0,z0)是直线上的一个点。 |
| distType | M-estimator 算法使用的距离 |
| param | 某些距离类型的数值参数(C)。 如果为0,则选择一个最佳值。 |
| reps | 足够的半径精度(坐标原点和直线之间的距离)。 |
| aeps | 足够的角度精度。 对于reps和aeps,0.01将是一个很好的默认值。 |
距离函数有:
轮廓的周长和面积
函数 arcLength 和 contourArea 可以用来计算点集所围区域的周长和面积
double cv::arcLength(InputArray curve,
bool closed
)
//Python:
retval = cv.arcLength(curve, closed)
double cv::contourArea(InputArray contour,
bool oriented = false
)
//Python:
retval = cv.contourArea(contour[, oriented])
参数 curve 和 contour 都为点集,closed 表示轮廓是否闭合,oriented 若为 true,则函数将根据轮廓方向返回带符号的值,默认为 false
点和轮廓的关系
函数 pointPolygonTest 可以实现点和轮廓(点集) 的关系。
double cv::pointPolygonTest(InputArray contour,
Point2f pt,
bool measureDist
)
//Python:
retval = cv.pointPolygonTest(contour, pt, measureDist)
| 参数 | 解释 |
|---|---|
| contour | 点集 |
| pt | 点 |
| measureDist | 是否计算坐标点到轮廓的距离 |
measureDist 如果为false,则函数的返回值有三种,即+1、0、-1,+1表示 pt 在轮廓内,0表示pt在轮廓上,-1表示pt在轮廓外;如果为true,则函数返回 pt 到轮廓的实际距离。
轮廓的凸包缺陷
通过函数 convexHull 可以得到点集的最小凸包,通过函数 convexityDefects 用来横来凸包的缺陷(凹陷)。
void cv::convexityDefects(InputArray contour,
InputArray convexhull,
OutputArray convexityDefects
)
//Python:
convexityDefects = cv.convexityDefects(contour, convexhull[, convexityDefects])
| 参数 | 解释 |
|---|---|
| contour | 轮廓(点集) |
| convexhull | 使用convexHull获得的凸包,其中应包含构成该包的轮廓点的索引 |
| convexityDefects | 返回的凸包曲线的信息,形式为 vector,每一个 Vec4i 代表一个缺陷,它的四个元素依次代表:缺陷的起点、终点、最远点的索引及最远点到凸包的距离。 |
int main()
{
string outdir = "./images/";
// 输入图像
Mat img = imread("手.png");
Mat gray;
cvtColor(img, gray, COLOR_BGR2GRAY);
// 边缘检测或阈值处理生成一张二值图
Mat gaussImg;
Mat binaryImg;
GaussianBlur(gray, gaussImg, Size(3,3), 0.5);
threshold(gaussImg, binaryImg, 0, 255, THRESH_OTSU|THRESH_BINARY_INV);
Mat kernel = getStructuringElement(MORPH_RECT, Size(5,5));
//形态学开运算(消除细小白点)
morphologyEx(binaryImg, binaryImg, MORPH_OPEN, kernel);
imwrite(outdir+"canny.jpg", binaryImg);
// 边缘的轮廓
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(binaryImg, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
Mat contourImg = Mat::zeros(img.rows, img.cols, CV_8UC1);
for(int i = 0; i < contours.size(); i++)
{
drawContours(contourImg, contours, i, Scalar(255), 2);
// 轮廓的凸包
vector<int> hull;
vector<Vec4i> defects;
convexHull(contours[i], hull, false, false);
convexityDefects(contours[i], hull, defects);
for(int j = 0; j < defects.size(); j++)
{
Point start = contours[i][defects[j][0]];
Point end = contours[i][defects[j][1]];
Point far = contours[i][defects[j][2]];
line(img, start, end, Scalar(0, 255, 0), 2);
circle(img, far, 5, Scalar(0, 0, 255), -1);
}
}
imwrite(outdir+"手.jpg", img);
imwrite(outdir+"手轮廓.jpg", contourImg);
}
对凸包的缺陷检测在判断物体形状等方面发挥着很重要的作用,与凸包缺陷类似的还有如矩形度、椭圆度、圆度等,它们均是衡量目标凸体形态的度量。