用 GAN 生成 MNIST 形式数字模式（Make Your First GAN With PyTorch 第7章）

• 本文是 Make Your First GAN With PyTorch 的第 7 章，本书的介绍详见这篇文章。

---

---

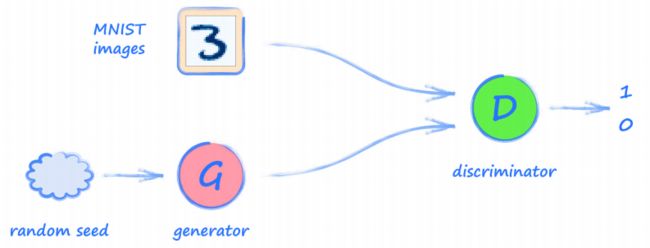
在上一章 自动生成简单的 “1010” 数字模式的基础上，本章介绍自动生成 MNIST 手写体数字的图像。

同样的，以任务的流程图开始：

架构和上一章的一样，真实图像是 MNIST 数据集（详见这篇文章介绍），生成器的目的是能生成和 MNIST 类似的图像。

创建新的 Python notebook 文件，导入需要的库：

import torch
import torch.nn as nn
from torch.utils.data import Dataset

import pandas, numpy, random
import matplotlib.pyplot as plt

• 本书前面几章，有 MNIST 分类器和自动生成 1010 数字模式的内容，这章可能直接拷贝相关代码。

1. Dataset 类

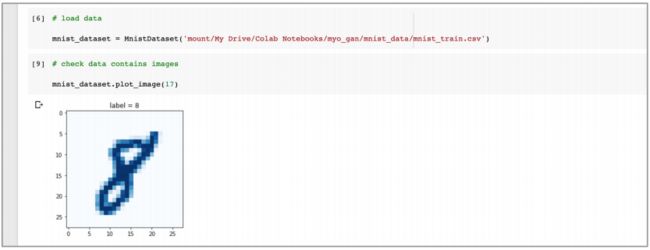
使用 PyTorch 的 torch.utils.data.Dataset 类，从源 CSV 文件中载入 MNIST 数据。这里直接使用之前的文章 中编写的 MnistDataset 类，不需要任何改变，代码如下所示：

class MnistDataset(Dataset):

    def __init__(self, csv_file):
        self.data_df = pandas.read_csv(csv_file, header=None)
        pass
        
    def __len__(self):
        return len(self.data_df)
        
    def __getitem__(self, index):
        # 图像标签
        label = self.data_df.iloc[index,0]
        target = torch.zeros((10))
        target[label] = 1.0 
        
        # 图上数据, 从 0-255 归一化到 0-1
        image_values = torch.FloatTensor(self.data_df.iloc[index,1:].values)/ 255.0
        
        # 返回图像标签、图像数据和目标
        return label, image_values, target
        
    pass

• 这个 MnistDataset 类，将数据打包为张量，并对每个图片记录返回 3 个值：一个 标签（label），一个归一到 0 到 1 之间的像素值，以及一个 one-hot 形式的 目标（target）向量。

下面进行测试：

2. MNIST 鉴别器构建与测试

2.1 MNIST 鉴别器

在 GAN 中，鉴别器其实是一个分类器，而前面已经针对 MNIST 图像构建了分类器。

同时，上一章也构建了 1010 数字模式的鉴别器，这里的鉴别器基本一致，仅神经网络尺寸不同。

下面拷贝1010 数字模式的鉴别器Discriminator 类的代码，但仅仅改变各层的尺寸，包括 forward()、train() 和 plot_progress() 等在内的其他函数都可以保持不变：

self.model = nn.Sequential(
    nn.Linear(784, 200),
    nn.Sigmoid(),
    nn.Linear(200, 1),
    nn.Sigmoid()
    )

2.2 测试鉴别器

同样，先测试构建的鉴别器能否将真实图像与随机噪声进行区分。

下面的代码使用 60,000 个训练数据的图像进行训练：

D = Discriminator()

for label, image_data_tensor, target_tensor in mnist_dataset:
    # 真实数据
    D.train(image_data_tensor, torch.FloatTensor([1.0]))
    # 虚假数据，使用了生成的随机数据进行训练
    D.train(generate_random(784), torch.FloatTensor([0.0]))
    pass

观察训练期间损失值：

可以看到损失值降到 0，并保持在接近 0 的水平。

通过将数据集中随机选择的一些图像，以及一些随机噪声的图像通过鉴别器：

• 可以看到真实的图像导致高输出值，这意味着鉴别器认为它们是真实的；
• 同样，随机噪声图像被网络赋予一个较低的值，说明鉴别器可以识别它们是虚假的。

3. MNIST 生成器构建与测试

3.1 生成器构建

• 生成器的目的是为了生成 MNIST 数据集中相同格式的图像（也就是 28*28，784 个像素值的图像）。

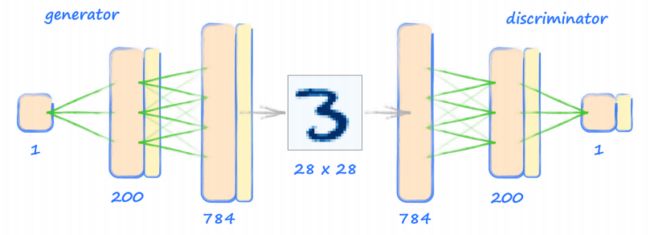
同样，首先将鉴别器的网络进行反转，也就是下图左侧 784 个输出，200 个节点的隐藏层和 1 个节点的输入：

在之前的 1010 GAN 中，生成器经过训练后，每次使用时都可以产生 1010 模式。 这里不希望生成器每次使用时总是产生相同的输出，而是希望它能产生不同的图像， 代表训练数据中的不同数字，比如数字 3，7，4，9 等。

由于神经网络对于给定的输入总是产生相同的输出。 这意味着要改变生成器以前使用的常数 0.5 的输入，下图体现了这个 随机种子(random seed)。

• 在知乎，有网友问过我类似的问题。需要注意的是，神经网络的训练部分是随机的，但是当训练完成后，给定输入的输出进行计算并不是随机的。

为什么在生成器中放入一个随机的种子能帮助它创建不同的图像呢？

• 这里先不回答，但可以预料到，生成器可能学会对不同的输入范围创建不同的输 出。例如，生成器可以通过学习，在输入值为 0.0 到 0.2 的范围内时创建一个数字 3 的图像，或者在输入值在 0.4 到 0.6 范围内时创建数字 9 的图像。

生成器代码基本直接拷贝自 1010 GAN，只是改变了神经网络层尺寸：

self.model = nn.Sequential(
    nn.Linear(1, 200),
    nn.Sigmoid(),
    nn.Linear(200, 784),
    nn.Sigmoid()
)

3.2 检查生成器的输出

在训练 GAN 前，检查生成器是否可以输出正确格式的图像：

G = Generator()
output = G.forward(generate_random(1))
img = output.detach().numpy().reshape(28, 28)
plt.imshow(img, interpolation = 'none', cmap = 'Blues')

• 上面的代码中，首先创建了一个新的生成器对象 G，然后使用一个随机种子输入，获得一个 output 常量，并将其尺寸重整为 (28, 28)，显示为图像：

可以看到，上图的尺寸是满足要求的，但是一个非常随机的图像。这也很正常，因为这时候还没有经过训练…

4. 训练 GAN

下面，训练这个网络，训练循环与前面的原理，以及 1010 GAN 一样，唯一变化的是给鉴别器和生成器的数据不同：

# 创建鉴别器和生成器
D = Discriminator()
G = Generator()

# 训练鉴别器和生成器
for label, image_data_tensor, target_tensor in mnist_dataset:

    # 训练的第一步：使用真实数据训练鉴别器
    D.train(image_data_tensor, torch.FloatTensor([1.0])
    
    # 训练的第二步：使用虚假数据训练鉴别器
    # 特别提醒：使用 detach()，使得生成器（G）中的梯度不被计算
    D.train(G.forward(generate_random(1)).detach(), torch.FloatTensor(p0.0]))
    
    # 训练的第三步：训练生成器
    G.train(D, generate_random(1), troch.FloatTensor([1.0]))
    pass

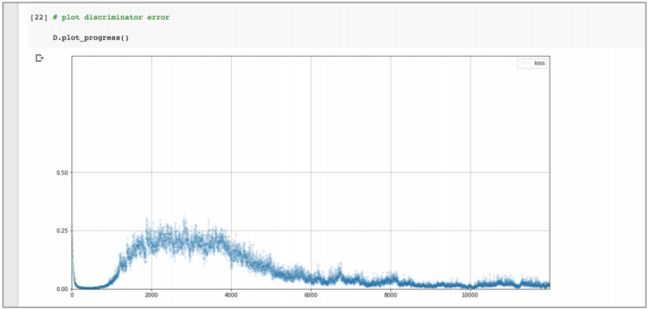
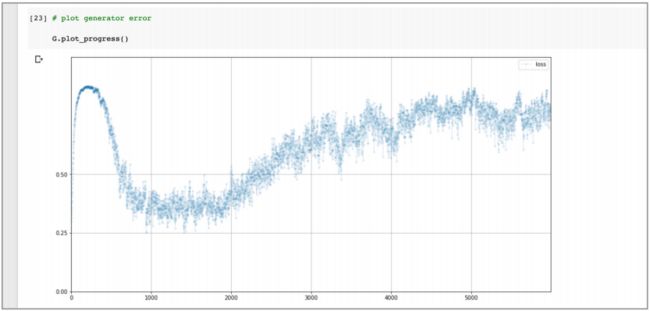
训练时间很短，下面给出训练鉴别器的损失值：

• 这个图表很有趣，损失值先降至 0，并在一段时间内保持在较低水平，这表明鉴别器走在生成器前面；然后损失值上升到大约 0.25 以下，这表明鉴别器和生成器是平衡的；不幸的是，鉴别器再次领先，损失值下降并保持在较低水平。

下面观察生成器训练时的损失值：

• 刚开始，鉴别器可以正确分类生成的图像，所以损失值变高；然后损失值下降 到 0.25 附近，说明生成器和鉴别器在一定阶段获得平衡；同样的在训练的后半段，随着鉴别器再次变得比生成器更强，损失会增加。

使用下面的代码，观察不同随机种子时，生成器生成的图像：

# 显示 3列，2行的生成的图像
f, axarr = plt.subplots(2, 3, figsize = (16, 8))
for i in range(2):
    for j in range(3):
        output = G.forward(generate_random(1))
        img = output.detach().numpy().reshape(28, 28)
        axarr[i, j].imshow(img, interpolation = 'none', cmap = 'Blues')
        pass
    pass

结果如下：

关于生成的图像，首先注意到的是它们不是随机噪声，而是具有确定的形状，图 像的中间是黑暗区域，就像手写数字的真实图像。

更好的，这个图像看起来并不包括任何可以识别的数字，可以说这个图像是一个 9，也可以看这个图像像 5。

• 虽然这个图像并不是一个完美的画出来的图像，但仍然使用一个很简单的代码获得了一个意义重大的里程碑。记住，生成器并没有直接看到 MNIST 数据集中的图像，但学会了创建非噪声的图像，这是可识别手写数字的开始！

进一步观察这些图像，可以看到 这些生成的图像看起来是几乎一样的。即使图像间有微小不同，这些不同点也一定小到难以分辨。

5. 模式坍塌（Mode Collapse）

很不幸，刚才看到的是在 GAN 训练中一个非常常见的问题，称之为 模式坍塌
(mode collapse)。

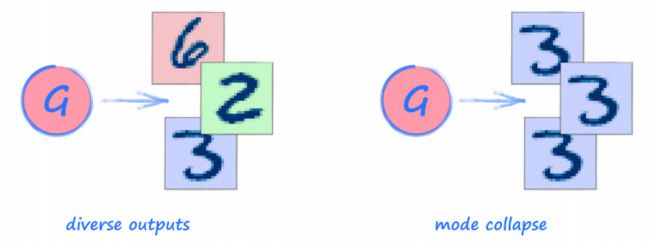
在本文中，我们期望的是生成器有能力生成所有十个数字的图像。但当模式坍塌发生时，生成器可能只产生一个或者很少数量的数字。上面的生成器一遍又一遍的生成相同的数字，所以它也在承受着模式坍塌。

• 模式坍塌发生的原因并没有完美的解释，相关研究仍在进行中，而且很活跃。
• 关于模式坍塌的一个看法是，在鉴别器学会向生成器提供高质量反馈之前，生 成器已经领先于鉴别器并找到一个始终被归类为真实的图像。
• 为了弥补这一点，一个很容易的方法是尝试更多去训练鉴别器，而不是生成器。但是在实践中，人们发现这并不奏效。这表明，解决办法不仅在于数量，还在于训练的质量。
• 在我们的例子中，生成器的损失值上升表明它没有学习，可能是因为鉴别器没 有很好地为它提供良好的反馈。这也再次表明，训练质量是一个挑战。

下一节将尝试一些改进鉴别器、提升生成器反馈质量的方法。

6. 改善 GAN 的训练

本节将尝试通过改善 GAN 的训练质量来解决模式坍塌和图像清晰度问题。

6.1 第一轮尝试

• 第一种改进是使用二进制交叉熵 BCELoss() 代替均方误差 MSELoss() 作为损失函数。

self.loss_function = nn.BCELoss()

前面已经讨论过，当网络执行分类任务时，二进制交叉熵 BCELoss() 的损失方法更有意义。二进制交叉熵 在惩罚不正确的答案和奖励正确的答案方面，比均方误差更为强烈。

• 下一个改进，是在鉴别器和生成器中使用 LeakReLU() 激活函数。

以前讨论过 LeakReLU() 激活函数如何减少大信号值的梯度消失问题，这是一种常用的提高神经网络训练质量的方法。
但实际操作中， 我们只在中间层之后应用它们，并在最后一层保留 Sigmoid() 函数，因为我们期望输出是在 0 到 1 之间。

• 另一种改进方法是将神经网络中的信号进行规范化处理（**normalise），以确保它们以平均值为中心，并限制其方差，以避免出现大的值使得网络饱和。

下面的代码描述了改进后的鉴别器神经网络：

self.model = nn.Sequential(
    nn.Linear(784, 200),
    nn.LeakyReLU(0.02),
    
    nn.LayerNorm(200),
    
    nn.Linear(200, 1),
    nn.Sigmoid()
)

生成器代码也进行了相应改进：

self.model = nn.Sequential(
    nn.Linear(1, 200),
    nn.LeakyReLU(0.02),
    
    nn.LayerNorm(200),
    
    nn.Linear(200, 784),
    nn.Sigmoid()
)

• 关于优化器，之前尝试过的另一个改进是 Adam 优化器，这里同时应用到鉴别器和生成器上：

self.optimiser = torch.optim.Adam(self.parameters(), lr = 0.0001)

观察一下上面 4 个改变的结果：

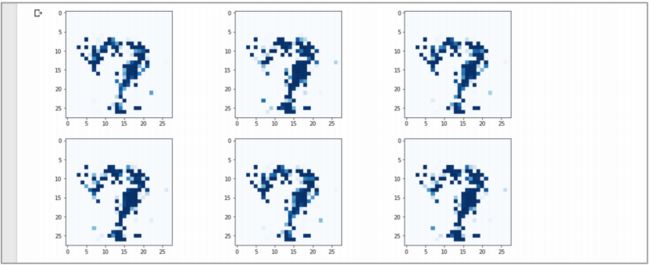
遗憾的是，仍然有模式坍塌。虽然图像本身更清晰，结构更清晰，但仍然不是一个明显的数字。

6.2 第二轮尝试

下面更深入地思考一下如何改进 GAN 的架构。

**生成器的起点是种子。**最早，我们使用的种子是常数值 0.5，然后把它改成一个随机 值，因为任何神经网络对于固定的输入总是给出相同的输出。

不过，也许生成器的神经网络很难将单个值转换为能表示数字的 784 个像素值，所以我们我们可以通过提供更多的输入种子来优化，比如可以尝试采用 100 个输入节点，每个节点都是随机值。

下面是更新后的生成器的定义：

self.model = nn.Sequential(
    nn.Linear(100, 200),  # 注意观察输入节点的变化
    nn.LeakyReLU(0.02),
    
    nn.LayerNorm(200),
    
    nn.Linear(200, 784),
    nn.Sigmoid()
)

观察这个修改的效果：

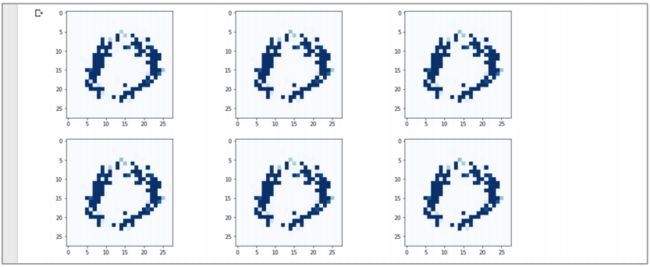
图像更清晰，看起来更像手写数字，这些特定的输出看起来像数字 0。

但遗憾的是， 所有生成的图像实际上还是相同的，我们还在承受模式坍塌的痛苦。

6.3 第三轮尝试

没关系，即使是最优秀的 GAN 研究人员也在与模式坍塌作斗争！我们继续！

继续深入思考，如果继续考虑给到生成器和鉴别器的随机种子，其实它们应该是不同的。

• 对于 鉴别器 而言，提供给鉴别器作为图像像素值的随机值，应该在 0 到 1 的范围内均匀挑选。原因如下：①挑选的范围是 0~1 是因为这是真实数据集像素值的范围；②选择均匀值，是因为我们是在中立随机性下测试鉴别器的性能，所以应该选择均匀值，而不是像正态分布那样有偏差；
• 对于 生成器 而言，提供给生成器的随机值不一定非得在 0 到 1 的范围内。原因如下：①中心为 0 且方差有限的归一化信号有助于训练，而且之前在 Make Your Own Neural Network 中探讨了这个问题，可以用它初始化神经网络的权重，所以这里选择以 0 为中心、方差为 1 的随机正态分布。

基于上述考虑，将生成随机数据的函数分为两个，分别为 torch.rand() 和 torch.randn() 两个：

def generate_random_image(size):
    random_data = torch.rand(size)    # torch.rand() 是生成均匀分布的函数
    return random_data
    
def generate_random_seed(size):
    random_data = torch.randn(size)    # torch.randn() 是生成标准正太分布的函数
    return random_data

实际使用时，我们将函数 generate_random_image(784) 提供给鉴别器，而将函数 generate_random_seed(100) 提供给生成器：

D = Discriminator()
G = Generator()

# 训练鉴别器和生成器
for label, image_data_tensor, target_tensor in mnist_dataset:

    # 使用真实数据训练鉴别器
    D.train(image_data_tensor, torch.FloatTensor([1.0]))
    
    # 使用虚假数据训练鉴别器
    # 使用 detach()，使得 G 的导数不被计算
    D.train(G.forward(generate_random_seed(100)).detach(), torch.FloatTensor([0.0]))
    
    # 训练生成器
    G.train(D, generate_random_seed(100), torch.FloatTensor([1.0]))
    
    pass

观察这个改进是否能改进结果：

不错，看起来已经修复了模式坍塌问题，网络能够生成不同的数字。可以看到 图中的形状看起来像是数字 8、2 和 3，还有一些模糊不清的数字，一个看起来可能是 4 或者 9。

• 再次陈述一下已经取得的成就：我们训练了一个生成器来绘制数字图像，虽然生成器并没有直接看到任何真实的图像，但看起来像是从训练数据中提取出来的。
• 另外，一个经过训练的生成器只需改变随机种子，就可以产生多种数字。

这个成就很大，因为有时修复模式坍塌很困难，甚至很多时候并没办法。

6.4 进一步讨论

下面我们观察损失图表。

由于现在使用的是 BCELoss() ，损失值并不总是在 0 到 1 的范围内，所以需要更新鉴别器和生成器中的 plot_progress() 函数，以删除损失范围显示的上限，并添加更多的水平网格线。

def plot_progress(self):
    df = pandas.DataFrame(self.progress, columns=['loss'])
    df.plot(ylim=(0), figsize=(16, 8), alpha=0.1, marker='.', grid=True, yticks=(0, 0.25, 0.5, 1.0, 5.0))
    pass

下面是鉴别器在训练过程中的损失值：

• 可以看到鉴别器的损失值迅速下降到零，并保持在接近零，偶尔在训练中跳跃，
  这表明还没有在生成器和鉴别器之间取得平衡。

下面是生成器在训练过程中的损失值：

• 可以看到生成器损失值开始上升，这意味着生成器在训练初期落后于鉴别器；之
  后损失下降并保持在 3 左右。同时，需要注意的是和 MSELoss 不同，BCELoss 的上限不是 1.0。

初看起来，这两个损失值的图表可能看起来不太好，因为它们的损失值范围非常宽。

但实际上，随着上面的这些改进，损失值比之前更好了：比如，鉴别器的损失值相当整齐地下降到 0，也就是说这些损失值并没有分布在很大的范围内；同时，生成器的损失值同样整齐地上升。

这些整齐的上升下降看起来不错，但是生成器损失值的升高并不是我们想要的，我们需要搞清楚，在获得了均衡时，BCELoss 应该是什么样的。如果运行前面已经获得均衡的 1010 GAN，在使用 BCELoss 情况下，生成器和鉴别器的损失值应该大约在 0.69 左右。进一步，使用 二元交叉熵（binary cross entropy） 的数学定义，可以计算获得理想的损失值为 ln(2)，或者 0.693。

• 有关 二元交叉熵（binary cross entropy） 的更多信息，我们挖个坑，后面会详细讨论，欢迎大家关注作者。

虽然很幸运修复了模式坍塌问题，但是图像本身质量却一般。

下面使用更多的 epoch 进行更长的训练，观察图像质量能否有所改进。

代码中可以很容易地用一个外部的 epoch 循环来将 GAN 训练循环包括在内。

下面的图像是 4 个 epoch 后训练的结果，也就是使用了 4 次训练数据，大约需要30 分钟。

• 现在图像更好了很多。如果有时间的话，也可以使用 8 次训练 epochs，这将需要大约一个小时。

7. 使用多个种子进行实验

目前为止，给生成器提供的种子只是一个随机数，在一个 GAN 被训练之后，不同的 “种子” 可以获得一些有趣的特性。

7.1 种子的插值

设想两个不同的种子 seed1 和 seed2，可以使用这两个种子生成图像。现在设想一个在 seed1 和 seed2 中间的种子，那生成的图像将会如何呢？

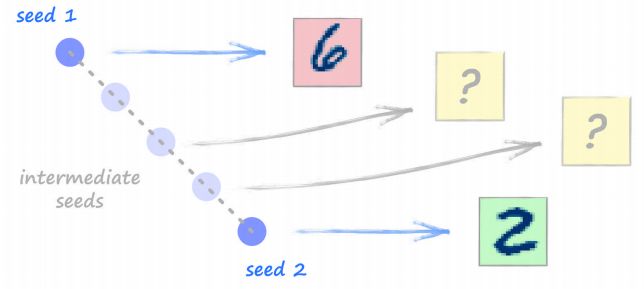
下面进行尝试。这里需要一个已经在 MNIST 数据上训练好的 GAN，可以使用之前的 notebook 文件。

首先，下面的代码选择一个随机种子，并将其保存为 seed1，便于后续使用（同时绘制种子的图像）：

seed1 = generate_random_seed(100)
out1 = G.forward(seed1)
img1 = out1.detach().numpy().reshape(28, 28)
plt.imshow(img1, interpolation='none', cmap='Blues')

下面的代码跟上面的一致，只是将种子保存为另一个种子 seed2：

seed2 = generate_random_seed(100)
out2 = G.forward(seed2)
img2 = out2.detach().numpy().reshape(28, 28)
plt.imshow(img2, interpolation='none', cmap='Blues')

• 当然，并不是每次运行生成器都能生成清晰的数字，所以可以重复代码来获得清晰的数字。

我自己而言，下面的图像由 seed1 和 seed2 生成，看起来像个数字 5 和 3：

下面的代码，计算在 seed1 和 seed2 间均匀分布的 12 个种子：

count = 0

# plot a 3 column, 2 row array of generated images
f, axarr = plt.subplots(3, 4, figsize=(16, 8))
for i in range(3):
    for j in range(4):
        seed = seed1 + (seed2 - seed1)/11 * count
        output = G.forward(seed)
        img = output.detach().numpy().reshape(28, 28)
        axarr[i, j].imshow(img, interpolation='none', cmap='Blues')
        count = count + 1
        pass
    pass

代码看起来可能很复杂，但它所做的只是从 seed1 和 seed2 方向执行 12 个 步骤，并绘制从相应的种子生成的图像。

可以看到，当种子从 seed1 向 seed2 变化时，图像或多或少地平稳地由数字 5 进化为 3。这是种子值的一个很好的属性。

7.2 种子的相加

如果两个种子相加，能获得什么图像呢？

seed3 = seed1 + seed2
out3 = G.forward(seed3)
img3 = out3.detach().numpy().reshape(28, 28)
plt.imshow(img3, interpolation='none', cmap='Blues')

代码很简单，使用 seed1 + seed2 创建了一个新的 seed3，然后提供给生成器：

• 这里的结果看起来像一个数字 8。这很合理，是因为我们如果将一个数字 5 和一 个数字 3 叠加的话，确实会比较像数字 8。这里也说明了种子的一个很好的特性，也 就是种子的相加带来图像的相加。

7.3 种子的相减

看完了种子相加的效果，那么如果它们相减呢?

seed4 = seed1 - seed2
out4 = G.forward(seed4)
img4 = out4.detach().numpy().reshape(28, 28)
plt.imshow(img4, interpolation='none', cmap='Blues')

结果是：

• 这个图像看起来像一个数字 5，但也像一个数字 6。这好像并不是像从数字 5 中 减去数字 3 那么合乎逻辑，所以种子的属性也许不那么简单。

7.4 其他的例子

下面尝试另一个例子，下面的图表显示了起始种子、插值种子、种子之和和种 子之差的图像：

• **非常奇怪！**可以看到两个起始的种子都给了我们相似的两个数字 9 的图像。在两个种子之间的插值也给出了 9 的图像，两个种子之和的图像也是 9。但是两个种子之差的图像是 8，好奇怪！

下面是另一个例子，两个种子的图像都是 5，但是两个种子差的图像是一个 3。

• 上面的例子这表明用种子做算术并不像想象中那么简单，并没有明确的逻辑来决定种子相加或相减时图像的形式。

8. 全文总结

经过冗长的全文后，总结如下几条：

• 对 黑白图像（monochrome images） 进行处理，并不需要改变网络的设计，二维的像素值数组很容易展开或者改变形状为一维的列表，并提供 给鉴别器。完成的方式不重要，一致性（consistency） 更重要；
• 模式坍塌（mode collapse） 是某个生成器可能产生多个输出时，但仅产生了一个输出。模式坍塌是 GAN 训练中最常见的一个挑战，其起因和解决方法还并没有很好被理解，仍然是研究的热点；
• 设计 GAN 的一个很好的起点是构建 镜像（mirror） 的生成器和鉴别器 网络结构，目标是对两者进行平衡，使得两者在训练时不会一个领先另一个太远；
• 实验表明，质量（quality），但不仅是质量，是 GAN 训练成功的关键；
• 在生成器 种子（seeds） 之间平滑的插值，会产生平滑插值的图像；对种 子相加看起来会相应的混合图像的特征；但是使用相减的种子，并不符合简单相减的模式；
• 理论上，完美的训练后的 GAN 理想的 MSE 损失值是 0.25，理想的 BCE 损失值则是 ln(2) 或大约 0.69。