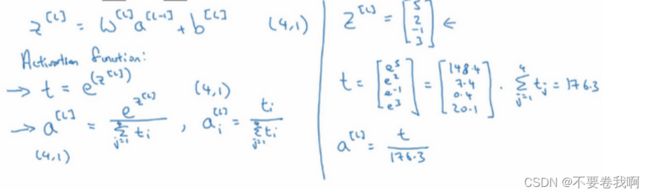【学习周报】深度学习笔记第四周
学习目标:
- 深度学习吴恩达lesson2-week3:超参数调试、Batch正则化和程序框架(Hyperparameter tuning)
- 深度学习吴恩达lesson3-week1:机器学习(ML)策略(1)
- 深度学习吴恩达lesson3-week2:机器学习(ML)策略(2)
学习内容:
目录
学习目标:
学习内容:
学习时间:
学习产出:
lesson2-week3
3.1 参数的统计与选择
3.2 参数合适的取值范围
3.3 Batch归一化
3.4 Softmax 回归
lesson3-week1
1.1 什么是机器学习(ML)策略?
1.2 正交化(Orthogonalization)
1.3 训练/开发/测试集划分
1.4 什么是人的表现?
1.5 可避免偏差(Avoidable bias)
lesson3-week2
2.1 进行误差分析
2.2 一些针对错误的小技巧
2.3 迁移学习
2.4 多任务学习
2.5 端到端深度学习的概念
学习时间:
10.17-10.21
学习产出:
lesson2-week3
在lesson2-week2这一周的学习中,我们又接触到了许多新的调整训练集合的方法,讨论了各种减小偏振误差,加快学习速度的方法。其中引入了许多的超参数。对于这些超参数的值的确定,或者说是选择,往往是需要大量分析的。所以week3我们讨论如何去分析这些参数,确定超参数的值从而得到更适应的模型。
3.1 参数的统计与选择
如图吴老师给出的各种常见的超参数。
1学习率a
2Momentum动量梯度下降法参数β
4如果使用Momentum或Adam优化算法的参数,β1,β2和ε
3层数layers
2隐藏单元个数
3学习率衰减
2mini-batch的大小m
(前面数字代表重要程度,标号越小越重要)
以上是我们分析出的一些超参数
下面讨论如何选择调试这些参数的值。
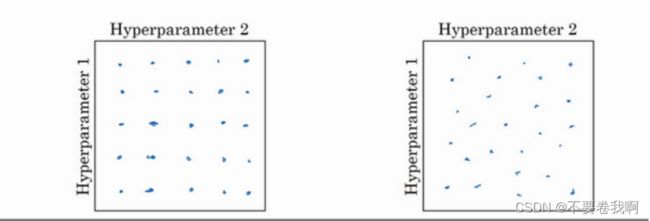
假设我们采用图一的方法:正方形选取25个点(两个变量的情况下),那么横向或者纵向两个变量其实仅仅只选取了5个值,优点是我们很容易就可以找出两个变量的最优选取值,例如控制某个变量不变,就可以很好的看出另一个变量的优劣变化从而选出结果。但是缺点是在多个变量互相影响的情况下效果不好。
采用图二方法:我们采取随机选取25个点的方法,那么不管是横向还是纵向取值都有25个不同。对于许多变量的情况,我们跟希望取到更多的不同的情况,这样我们就能探究更多的情况。
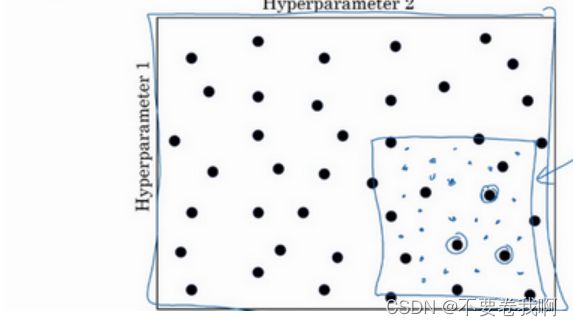
另外一种方法就是,我们在第一次实验结果基础上发下最优的点在某个更小的矩阵中,那么我们就可以在下一次取值中放在该小矩阵就继续运行,最终就可以确定最优解所在的某个小范围。
所以这种从粗到细的搜索也经常使用。
3.2 参数合适的取值范围
在上一个小节中,你已经看到了在超参数范围中,随机取值可以提升你的搜索效率。但随机取值并不是在有效范围内的随机均匀取值,而是选择合适的标尺,用于探究这些超参数,这很重要。
均匀取值并不是很好的方法。
如上图对隐藏单元,神经网络层数在50-100、2-4中的随机均匀取值是可行的。
但是有些变量是不可以等概率随机取值的,可以要在某些范围有所侧重。
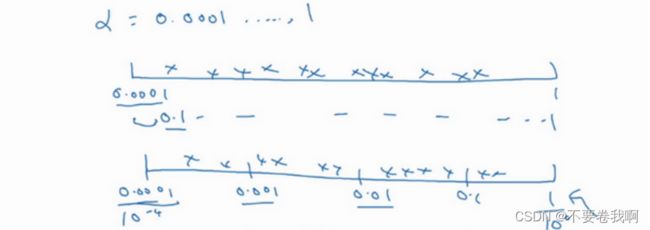
如上图,用对数标尺搜索超参数的方式会更合理,因此这里不使用线性轴,分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点,这样,在0.0001到0.001之间,就会有更多的搜索资源可用,还有在0.001到0.01之间等等。
那么为什么会这样,原因可以如下说明:学习率在0.0001-0.001中取值或许对于深度学习并没有太大影响,但是如果在0.1-1中选取会变得特别敏感,所以不使用均匀的随机选取有利于发现这种情况。
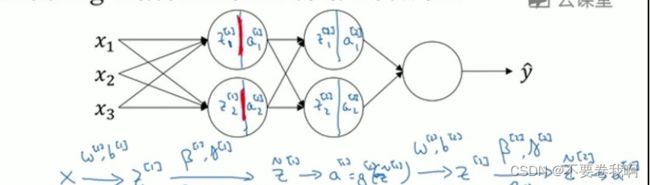
3.3 Batch归一化
让a或者z矩阵变得均匀分布的整体。
那么batch归一化为什么会有效呢?
首先,从之前的输入特征归一化可以看到,它可以将不同参数的范围变换到相似的范围,可以加速学习。但是batch归一化不仅仅是对输入值,而且还对隐藏单元进行归一化。
第二个原因是,它可以使权重比你的网络更滞后或更深层。比如第10层的权重比第一层的权重更能经受的住变化。这是什么意思呢?下面给出一个生动形象的例子。
对于下面这个猫脸识别的神经网路,可能是深层也可能是浅层。假设你已经在所有黑猫的图像上训练了数据集,如果现在你要把此网路应用于有色猫,这种情况下,正面的例子不仅是黑色猫还有有色猫。那么你的cosfa可能适用的不会很好(cosfa是啥意思?是classify吗?)。如果在黑猫图像中,你的训练集是一种情况,加上有色猫以后,如果你试图把黑猫和有色猫统一与一个数据集,那么你就不应该期待左边训练很好的模块同样在右边也运行的很好。
3.4 Softmax 回归
一种多分类的方法,可以理解成逻辑回归的复杂模型,回归的简化就是逻辑回归。
lesson3-week1
lesson3中主要涉及神经网络计算的训练,验证测试集合的准确率进行分析,并确定下一步应该如何改正提供思路。
1.1 什么是机器学习(ML)策略?
学习过程中,对于测试结果不满意,例如测试正确率90%我们应该如何改进做出的策略即我们现在要学习的内容。
1.2 正交化(Orthogonalization)
举一个简单例:当电视机的音量加与频道加两个键结合在一起时,我们没办法做到频道加且音量不变的情况,就会产生互相影响,正交化在机器学习中即代表如何消除这种影响。
如上图,即我们实现正交化,确保知晓调整某些参数改变一个功能。
1.3 训练/开发/测试集划分
在一般情况下,我们尽量使得训练集与测试集来自同一分布。
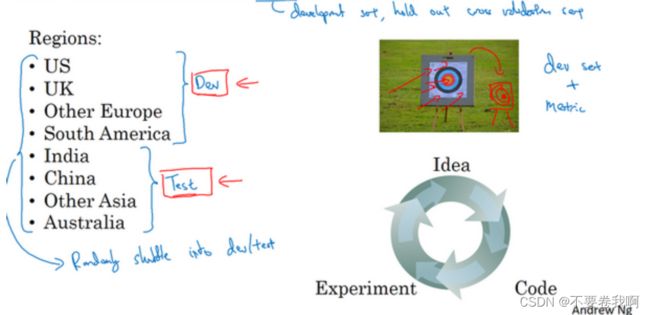
理由:以辨别猫的问题为例,假设各个国家的猫都有数据获得。
上图中我们将前四个国家与后四个国家分别用作训练、测试集,,那么测试集的准确率可能下降,原因时各个国家的猫可能因地域不同而有不同的特征,我们使用南美的猫图片去识别印度的猫咪图片,可能降低识别准确度。
为了抹平这种地域差异带来的学习影响,我们可以打乱各个数据,均匀分配。
1.4 什么是人的表现?
我们的深度学习最终目的是模拟人类大脑,或者超越人类大脑。
以识别猫为例,人在识别猫的准确率上的表现,往往是我们能够训练达到的大概上限。
这里引出贝叶斯最优错误率的概念
随着时间的推移,当您继续训练算法时,可能模型越来越大,数据越来越多,但是性能无法超过某个理论上限,这就是所谓的贝叶斯最优错误率
贝叶斯错误率一般高于人类的行为表现,但是两者都是用于估计我们训练的模型距离理论还有多少的差距。
1.5 可避免偏差(Avoidable bias)
在以前的讨论中,假设验证集合的错误率为10%,我们会认为偏差有10%那么多,因为在当时我们认为人的正确率可以高达100%,错误率为0,所以机器学习距离最优结果的偏差为10%,我们称这个偏差叫做可避免偏差。
lesson3-week2
在lesson-week1中的课程学习可能在深度学习中遇到的误差问题,接下来我们细致了解这些误差问题,并且讨论如何针对各种问题提供大体解决思路。
2.1 进行误差分析
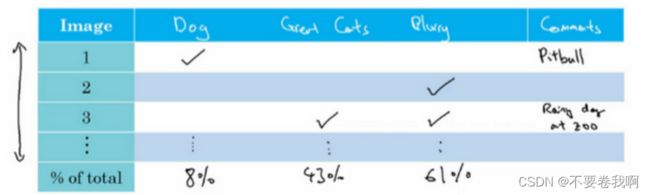
假设在搭建好的深度学习网络中,识别猫的正确率为90%,这里我们对于识别错误的10%做出讨论:
假设我们10%错误率中有0.5%把狗识别成了猫,那么我们修改神经网络对狗的识别程度,对网络改进并不会很好。
假设我们10%错误率中有9%把狗识别成了猫,那么改进网络让他对狗猫的识别特征更具体,就能很好的改进该系统。
这个样本里狗的问题是否值得解决。有时你在做错误分析时,也可以同时并行评估几个想法,比如,你有几个改善猫检测器的想法,也许你可以改善针对狗图的性能,或者有时候要注意,那些猫科动物,如狮子,豹,猎豹等等,它们经常被分类成小猫或者家猫,所以你也许可以想办法解决这个错误。或者也许你发现有些图像是模糊的,如果你能设计出一些系统,能够更好地处理模糊图像。
2.2 一些针对错误的小技巧
一、如果本身的训练数据中就存在错误的标签,例如:将本身不是猫的图片标记成猫。有以下考虑:如果数据量足够庞大并且标记错误对识别的正确率影响不大,可以不考虑标记错误的标签。如果数据量很小或者人工修改数据变成正确数据对于模型的识别正确率影响很大,可以考虑人工重新标签。
二、多多人工观察是否存在错误标签,以及正确的标签是否也需要改进。人工的检查有时候对模型的训练很有帮助。
三、快速搭建训练模型。只有动手确定训练的数据集合并且着手训练,才能更好更快的发现错误并且根据经验进行改正。
2.3 迁移学习
迁移学习:指在原本具有某一功能的基础上,将该模型的输入,输出进行修改并直接应用于其他模型。
适用场景:待解决的问题提供的数据很少。有类似的大量数据模型已经训练出很好的模型。
优点:新模型可以在旧模型的基础上直接应用或者稍微改进,便可以很好的应用。可以获得旧模型的大量数据提供的特征。
例子:计算机视觉的图像识别模型已经很成熟,可以很好的适用于放射性图像检查(放射性图像检查的数据一般很难获得或者说很少)。
2.4 多任务学习
在自动驾驶识别车辆的问题中,我们很常见的是在车辆照片中还会出现行人、红绿灯等特征。我们可以尝试选择一种方法对三种或者四种特征同时进行学习。
2.5 端到端深度学习的概念
在深度学习中我们往往有许多的层级,例如识别人脸有图片获取、特征提取、人脸定位等多个步骤。端到端学习的概念提出:是否可以省去这些步骤,让机器自己去理解图片。
优点:为机器自主学习提供了更全新的概念。可以让机器自己去理解数据的信息而不是学人类。例如音标是人创造出来的,或许没有音标机器也可以很好的学习各种语句。