图神经网络入门(理论篇)

图(Graph)

图结构是一种在我们日常生活中常见的结构，很多问题本质上都是图，比如复杂的分子结构以及社交网络等等。一般来说，图最核心的两个组成部分就是节点(node)和边(edge)。节点是图中的一个个个体，比如社交网络中的每个用户，而边用来描述节点与节点之间的连接关系。

图神经网络(GNN)

图神经网络是一种专门用于处理图结构或网络结构数据的神经网络模型，它的核心思想是基于每个节点的邻接节点的表征信息以及自身现有的节点表征来不断进行表征学习(node representation learning)。每经过一层神经网络就会去聚合自身节点以及相邻节点的表征信息做一次非线性变换。

经典GNN之图卷积神经网络(GCN)

就如同卷积这个名字一样，GCN 将图像中广泛应用的卷积方法迁移到图数据上，图像(Image)中的一个个像素点类比到图(Graph)上的一个个节点(node)。简单来说，即对于图中的每一个节点，我们直接去将其所有卷积范围内的相邻节点的表征，包括现有自身节点的表征进行融合来更新当前节点的表征。

具体来说，GCN的整个算法流程可以总结为1.传播 2.聚合 3.非线性变换 三个步骤。传播指的是图中的每一个节点接收所有相邻节点的节点表征信息。聚合指的是每一个节点将接收到的相邻节点的表征信息(包括自身节点信息)进行融合操作, 这里的融合范围可以理解为CNN的感受野，不同节点共享卷积核权重。每一层神经网络都对应一次聚合过程。第一层神经网络会将节点的直接邻居节点的表征融合进来，到第二层神经网络的时候，由于邻居节点已经融合了邻居的邻居节点的表征，因此在更新该节点的时候其实已经考虑到更大范围的邻域信息。神经网络的层数越多，节点更新融合的邻域范围就越大。对聚合后的的节点表征作非线性变换, 和MLP一样，用于增加神经网络的表达能力。

我们来看一下论文《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》中的具体公式:

首先，上式描述了基于图卷积网络结构的图中所有节点在l层的表征H(l)到l+1层表征H(l+1) 的变换过程。

上式中的H(l) 表示第l层的全部节点的表征，假设整个graph上总共有N个节点，每个节点的表征是一个D维的向量，那么H(l) 就是一个N*D维的矩阵。上式中的A矩阵是邻接矩阵，用于存储图中的每一个节点与图中其余每个节点的连接关系，存在连接即为1，不存在连接即为0，它的尺寸为N * N。但是如果仅关注其余节点显然是不合理的，节点表征在下一层的更新同样需要参考当前自身节点的表征，所以这里A矩阵会加上一个单位矩阵(identity matrix) 用来描述节点自身的"自连接"。最终这里的A 矩阵与 H(l) 矩阵的相乘就代表每个节点每个维度在下一层的值等于与该节点相连的所有节点在该维度值的和。但是这样显然不太合理，如果某个节点连接的节点很多，那么最终的更新值就会比那些孤立节点的值大很多。因此为了拉齐每个节点表征的尺寸，所有我们这里使用矩阵D， 即度矩阵来做归一化。最后矩阵W 是我们神经网络的可训练参数，sigma 代表激活函数，没啥好说的了。

神经网络的每一层都通过上述方式对节点表征进行更新直到最终的输出层。

经典GNN之GraphSAGE

上面提到的GCN需要将整张图的数据用于学习节点表征，是一种典型的转导学习(transductive learning), 其有两个比较大的缺点：1.当图结构发生变化时，更新节点的表征每次都需要对全图进行学习，资源消耗大。2.当我们使用转导学习的方法对节点进行预测时，该待预测节点必须包含在训练图中。但是很多时候，我们需要的是对未见过的新节点甚至是新图进行表征学习以及类别预测，对于这些场景，转导学习无能为力。

因此我们需要一种全新的类似于归纳推理的学习模式，类似于我们在已有的图上学习构建模型，该模型可以应用到其他的图上的节点表征预测。而GraphSAGE 就是这样一种归纳学习的模型。

首先GraphSAGE和GCN 相同点在于，二者都是通过对邻居节点的表征进行聚合操作来学习当前节点的表征，不同的是GraphSAGE 不仅仅局限于学习节点表征，更重要的是基于训练图数据去学习以及归纳出如何基于周围节点的信息聚合得到该节点的表征，学习到的参数可以在不同的图上进行共享。

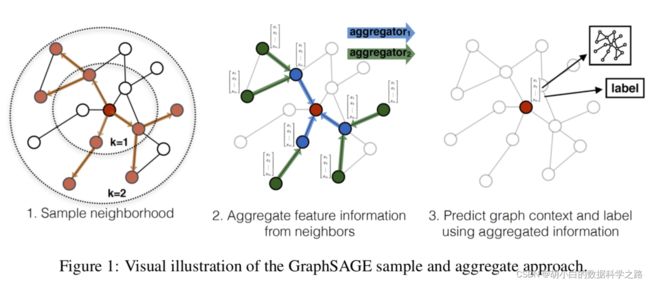
具体来说，GraphSAGE 的算法核心可以分为2个部分，一是采样(sampling), 二就是聚合(agg)。首先来说采样，和GCN的全图采样不同，GraphSAGE对于每个节点的学习并不基于所有邻居节点，而是随机抽样。作者总共采样K层，其中第一层代表直接邻居，第二层代表与当前节点的邻居相邻的节点层，依次类推。在原文中，作者提到取K=2 且 S1.S2 < 500( S1,S2 分别指每一层的采样节点个数) 就能取得很好的效果。在实际情况下，可能存在某些节点的邻居个数很少，这时就会对邻居节点进行重复采样。

然后就是聚合，聚合的逻辑就是从最外层节点逐渐向里聚合，当K=2 时，就是先聚合二阶邻居的特征，生成一阶邻居的embedding, 然后再聚合一阶邻居的embedding生成目标节点的embedding。作者在文中共提到了3种可行的聚合方式，分别是：
1.均值聚合：将采样的s个邻居节点表征分别与目标节点进行concat后得到s个表征，然后再对这s个表征进行按位平均后通过全连接网络并激活。

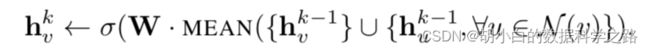
2.LSTM聚合：将邻居节点的embedding随机排列后作为LSTM结构的输入。使用LSTM的优点是具有更大的表达能力，但是本质上来说，LSTM处理序列数据并不满足排列不变性。
3.池化聚合：将均值操作换做max_pooling。

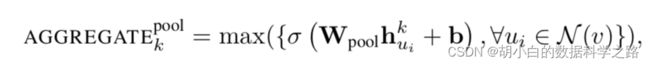
当完成了采样和聚合后，最后我们再将生成的目标节点embedding输入全连接网络并输出预测值。

下图展示了一个简单示例

经典GNN之GAT

同样是将邻居节点进行聚合，GAT 引入注意力机制，来给不同的邻居节点分配不同的权重进行聚合操作。

1.首先通过一个共享权重矩阵W，将每个节点的低维表征h 映射到高维表征h’。
2.将目标节点的每个邻居节点j= 1,2,3,…,n 的表征h’[j] 与 目标节点i表征h[i] 进行拼接 得到 j个表征。
3.通过一个前馈神经网络a(.) 将上述每个表征映射到一个实数上，该值即为注意力权重。

4.将不同邻居节点得到的注意力权重再进行一次softmax，即成为最终的聚合权重。

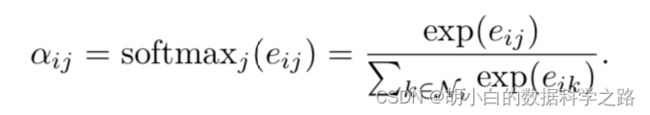
5. 最终，每个邻居节点基于得到的聚合权重，进行聚合，得到目标节点的表征。

当然和Transformer中一样，我们也可以使用多头注意力机制，即训练多套权重，然后进行concat或者均值操作。

以上就是3种基本图神经网络的基本介绍，在下一篇文章中，我会基于pytorch说明这三种网络的具体实现。