以不变应万变：因果启发的稳定学习年度研究进展（上篇）

【前沿进展】机器学习技术在计算机视觉、自然语言处理等领域得到了广泛的应用。然而，当下的机器学习技术大多以挖掘数据的关联性为基础，可能会带来稳定性、可解释性、公平性等方面的一系列不足。因此，如何将因果统计融入机器学习的框架，成为了一个具有挑战性的基础问题。稳定学习的目标正是寻找机器学习和因果统计的共同基础。

在近期的报告中，来自清华大学计算机系长聘副教授、智源青年科学家崔鹏，浙江大学计算机学院副教授况琨，来自清华大学计算机系的 4 位博士张兴璇、徐韧喆、刘家硕和何玥介绍了稳定学习理论和方法的年度进展，以及在解决分布外（OOD）泛化问题方面的机会和挑战。

本期整理自智源LIVE，报告详情、视频回放和PPT下载：

https://event.baai.ac.cn/activities/181

演讲者：崔鹏、况琨、张兴璇、徐韧喆、刘家硕、何玥

整理：熊宇轩

编辑：李梦佳‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

---

01

清华大学崔鹏：关于分部外泛化和稳定学习的一些思考

近年来，分布外（OOD）泛化问题广泛引起了机器学习和计算机视觉等领域研究者的兴趣。以监督学习为例，我们希望找到一个模型 f 以及其参数 θ，使得我们能够在测试数据分布上最小化和y之间损失的期望。

原则上说，我们测试时的数据分布是未知的，为了对其进行优化，传统的机器学习方法认为训练数据和测试数据满足独立同分布假设，从而对问题进行简化，使我们可以在训练数据分布下搜索带有参数 θ 的函数 f。

然而，这种简化的问题设定无法满足许多实际应用场景的要求，我们往往很难保证测试时和训练时的数据分布一致。通过上述方式学习到的缺乏理论保障，模型在真实的测试环境下的性能与实验室中训练时的性能可能相差甚远。为此，一些研究人员开始研究分布外场景下的学习问题。

根据测试时数据分布的不同，分布外学习问题衍生出了两条技术路径：（1）分布外域自适应：测试数据（目标域）部分已知，基于域自适应/迁移学习技术，将利用训练数据（源域）得到的模型适配到不同的数据分布（目标域）下（2）分布外泛化：测试数据分布完全未知。

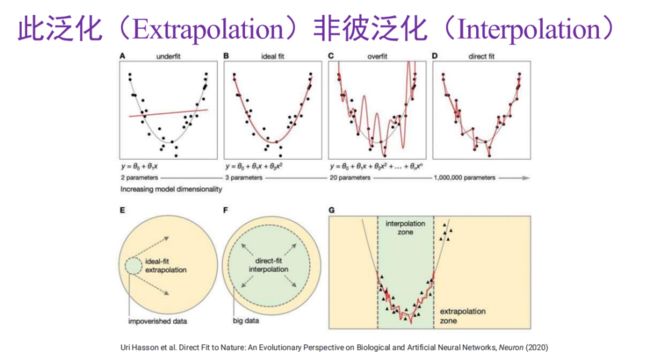
在传统的独立同分布学习场景下，模型泛化是一种内插（Interpolation）泛化，在分布外学习场景下，模型泛化则指的是外推（Extrapolation）。

如上图所示，在独立同分布场景下，如果 参数量太少，则模型对数据欠拟合；若参数量过多，则模型可能对数据过拟合。论文「Direct Fit to Nature：An EvolutionaryPerspective on Biological and Artificial Neural Networks」的作者认为，过参数化的深度学习网络之所以具有较好的泛化能力，可能是由于模型用类似折线的形式直接对数据点进行了拟合。

如果我们直观测到整体中很小的一部分数据，就需要对未观测到的数据进行外推。传统上，我们需要进行精巧的实验设计，基于小量的观测数据推理出分布外的情况。在这一过程中，我们会引入大量人类总结出的一些通用规律，从而实现数据的外推。

 

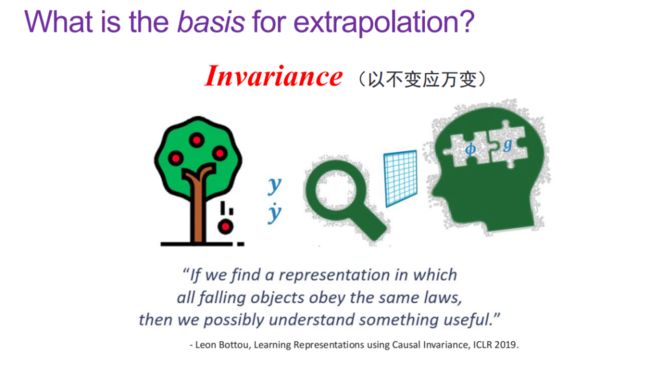
正所谓「以不变应万变」，「不变性」（invariance）是实现外推的基础。例如：牛顿观察到苹果从树上落下，从而推导出万有引力定律，进而可以将这一规律外推到其它物体的运动上。

在独立同分布场景下，由于我们认为训练数据和测试数据分布相同，我们的目标是数据拟合，此时「相关性」自然成为了一个很好的统计指标。在 OOD 场景下，我们旨在通过以下两条路径寻找「不变性」：（1）因果推理（2）从变化中寻找不变性

因果推理

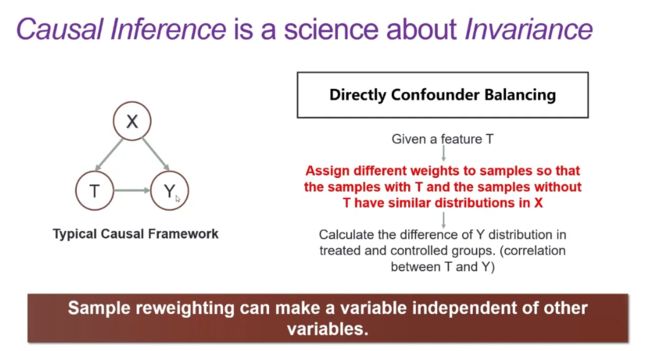
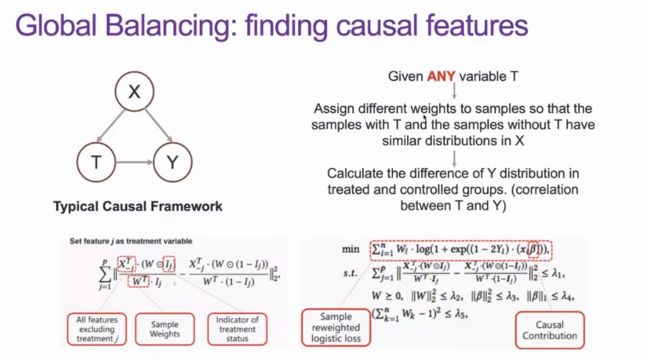
因果推理是一种与不变性相关的科学。在经典的因果模型中，我们试图控制X，寻找 T 的变化对 Y 的影响。具体而言，利用观测数据，我们会通过样本重加权（Sample Reweighting）将 T=1 和 T=0 时的样本具有相似的 X 分布，如果这两种情况下的 Y 有显著变化，则 T 对 Y 有因果效应。此时，我们估计出的 T 对 Y 的因果效应平均而言对于 X的变化是具有不变性的。

为了将不变性适配到学习框架中，我们要研究多个输入变量对输出变量预测性的影响。在稳定学习框架下，我们试图找到一组合适的样本权重，进行样本重加权后再通过输入变量对输出变量进行回归，此时的回归系数即为满足因果关系的回归系数。通过上述方式训练出的模型具有 OOD 的泛化能力。

从变化中寻找不变性

变化与不变性是对立统一的。在机器学习场景下，数据中的「变化」指的是训练数据中存在的异质性（例如，图像背景的不同、物体品类的不同）。然而，我们无法手动定义这种数据的异质性，因为我们无法保证数据在所有的特征维度上都满足不变性约束。

因此，一种可行的方式是从潜在的异质性中寻找不变性。我们假设环境是未知的，存在一定的异质性。在这种情况下，我们首先需要发现数据中的异质性，再根据数据的异质性发现其中的不变性，接着我们还可以反过来利用不变性提升对变化部分（异质性）的学习效果，这一过程将一直迭代下去。

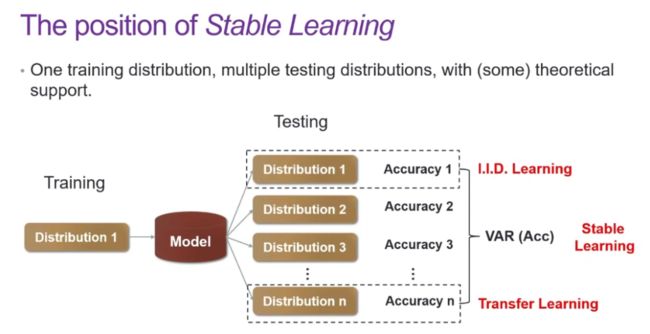
稳定学习的定位

在稳定学习框架下，我们利用一个异质的数据分布学习模型，希望将学习到的模型应用到一系列未知数据集上时具有一定的性能保证。除了通过实验证明此类模型的有效性，我们还希望为其发展出理论的支撑。（详见清华大学崔鹏组稳定学习综述：https://arxiv.org/abs/2108.13624）

02

清华大学张兴璇：StableNet——用于分布外泛化的深度稳定学习

我们具体来讨论深度稳定学习，比如我的训练图片中是很多狗都在草地上，然后少量的狗在其他背景上时，那么它需要能及及时分辨出草地上的狗，通常这个模型可以给出比较准确的预测。但是当给到一个他建的比较少的背景，他可能就会不一定给出一个准确的预测，但大部分可能还可以给出类似的预测，但是当它出现了一个他完全没有见过的背景的时候，这个模型很有可能就给出一个错误的预测。所以说这种分布偏移的问题，会给现在的深度网络带来很大的挑战。

对于当下基于独立同分布假设开发的深度学习网络而言，若训练数据和测试数据分布不一致时，模型的泛化性能将会较差。如上图所示，假设训练集包含大量背景为草地的狗，如果在测试时面对一张站在草地上的狗的图片，网络一般可以准确地对图片进行预测；然而，如果测试图片中的背景在训练集中出现地较少或从未出现，则网络的预测效果很可能较差。这种分布偏移问题是当前的深度学习网络面临的重大挑战之一。

之所以会出现上述问题，是因为网络学习到的很可能是数据之间的相关性。在上图中，由于训练集中大量存在「狗站在草地上」的样本，因此草地的特征和狗的图像特征之间建立了关联，进而在草地的特征和狗的标签之间建立了关联，导致在测试集上对其它背景图片的预测性能有所下降。

为了解决上述问题，我们试图转而抽取因果特征（例如，部分和整体的因果关系）。在稳定学习框架下，我们重点关注的是物体本身的因果特征，而非环境的特征。

如上图所示，ResNet18（第二行）网络不仅关注狗的特征，也关注到了背景的无关特征，而 Stable Net 则主要关注狗本身的特征。

具体而言，我们采用全局平衡（Global Balancing）方法提取因果特征。给定任意的干预（treatment），我们对训练样本进行加权，从而消除各类特征之间的统计关联性，断开背景与因果特征之间的关联，最终找到更加具有因果关系的特征，实现更加稳定的预测。

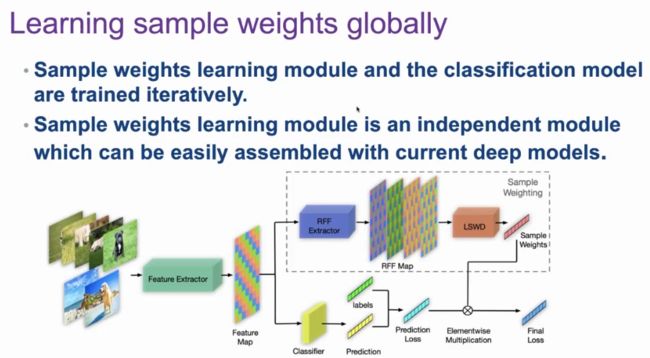
先前的稳定学习方法主要针对较简单的模型（例如，线性模型）开发，考虑的问题主要是消除特征之间的线性相关性。然而，在深度网络中，各类特征之间的相关性通常是非常复杂的非线性相关性。因此，StableNet 首先将所有的特征映射到其随机傅里叶特征的空间中，该步骤将较低维度空间中的特征映射到较高维度的空间中；接着，我们在较高维度的空间中去掉各类特征的线性相关性；这样以来，我们就可以去掉原始的特征空间中特征之间的线性相关性以及非线性相关性，保证特征的严格独立。

此外，原始的全局重加权方法需要对所有的样本进行操作。然而，在深度学习场景下，训练样本量一般非常大，我们无法对全局样本进行加权。为此，我们提出了一种预存储的方式，将网络之前见过的特征和样本权重存储下来，进而在新的一轮训练中结合当前的特征进行重加权。

StableNet 的网络架构如上图如所示。网络架构有两个分支，下面的分支为基本的图像分类网络，上面的分支是对样本进行 RFF 映射后再进行重加权的过程。我们可以将两个分支分离开来，从而将StableNet 插入到任何深度学习架构中。

目前，在计算机视觉领域的域泛化任务中，我们往往假设训练数据中的异质性十分显著，且各个域的样本容量相当。这在一定程度上限制了在 CV 领域中对 OOD 泛化方法进行验证。

本文作者基于 PACS 和 VLCS 两个数据集构建了各个图片域数量不平衡的实验环境，有一些图片域占据主导地位，具有更强的虚假关联。在该设定下，StableNet 相较于对比基线具有最佳的泛化性能。

在更加灵活的 OOD 泛化场景下，不同类别的图像所处的域可能不同。在该场景下，StableNet 的性能仍优于所有的对比基线。

在对抗性 OOD 泛化场景下，域和标签的虚假关联很强（例如，训练集中的大部分数字 1 的颜色为绿色，数字 2 为黄色；在测试时两种数字的颜色与训练集中相反）。StableNet 在几乎所有的实验设定下都超过了现有的方法。

03

清华大学徐韧喆：稳定学习——对协变量迁移的理论分析

目前，稳定学习算法已经在一些深度学习任务中展现出了对协变量偏移泛化的有效性，但是相关的理论分析仍较为有限。在本文中，作者将稳定学习算法解释为一种特征选择机制，选择出来的特征是能够解决协变量泛化问题的最小且最优的集合。具体而言，「最优」指的是选择出来的特征可以有效解决协变量偏移问题；「最小」指的是忽略无关变量，消除其在协变量偏移场景下的负面影响。

研究背景

协变量偏移泛化

「协变量迁移」指的是测试和训练数据中输入特征 x 的分布不同，而特征 x 对标签 y 的产生机制不变。「协变量迁移泛化」问题要求测试时的数据分布和训练时的数据分布存在协变量迁移，且测试时的数据分布未知。

稳定学习算法

通常而言，稳定学习算法包含以下两个步骤：

（1）重要性采样：学习一组样本权重，使得新分布中的各维变量严格相互独立（2）加权最小二乘：利用重要性采样学习到的样本权重训练加权的最小二乘回归模型。

现有的常见稳定学习算法包括：

（1）DWR 算法，学习一组样本权重，使任意两个特征之间线性无关

（2）StableNet：引入随机傅里叶特征机制，使变量之间在深度学习场景下严格独立

（3）SRDO：明确目标分布，并采用密度比估计进行重要性采样，学习样本权重。上述算法通过不同的方式学习出使 X 更为独立的加权函数。

在本文中，作者假设数据满足严格正密度假设，即将输入样本的不同特征维度所有取值的组合都有可能发生，即：

协变量偏移泛化的最优、最小变量

最优变量集合 S 是X 的子集。给定训练数据分布，训练算法 L，评价指标 M，最优变量 S 在预测 Y 的任务中可以得到最优的 M。最优且最小的变量指的是最小的 S 子集。

在严格正密度假设下，对于一些常见的损失函数（例如，MSE 损失，二分交叉熵损失）往往是使得评价指标 M 最大的最优解。令 S 为 X 的子集，则：

（1）当且仅当时，S 为分布下对 Y 的最优变量，我们将这样的 S 定义为稳定变量集合。

（2）当且仅当且沒有满足时，S 为分布下对 Y 的最小且最优变量，我们将这样的 S 定义为最小稳定变量集合。

可以证明，在严格正密度假设下，最小稳定变量集合是存在且唯一的。稳定学习的目标正是针对协变量迁移泛化问题寻找一组最小且最优的变量。

稳定学习算法的理论分析

如前文所述，在稳定学习算法框架下，我们首先要寻找一组采样权重，使重加权后的各位特征X严格独立，进而通过加权最小二乘让模型拟合独立的数据。进一步，我们可以将学习到的加权后的系数看做对特征的选择，将稳定学习解释为一种特征选择算法。具体而言，若非零，则选用对应的，否则就剔除对应的。

可以证明，在理想情况下（样本量无限大，准确学习到样本权重），若不在最小稳定变量集合中，则对于任意的，稳定学习算法可以剔除特征。若在最小稳定变量集合中，则存在，通过稳定学习算法可以找到特征。

与马尔可夫毯/边界的对比

相较之下，马尔科夫边界要求，即严格的条件独立；而最小稳定变量集则要求条件线性无关。在因果图中，在一定的假设下，马尔科夫边界可以解释成变量 Y 的父节点、孩子节点和兄弟节点，它对应能够预测 Y 的最小集合，该预测定义在上。

可以看出，最小稳定变量集合是马尔科夫边界的子集。但是在协变量迁移泛化场景下，并不一定需要满足马尔科夫边界的要求。相较之下，最小稳定变量集合要求评价指标 M 在被精确估计时取最大值，而马尔科夫边界则要求评价指标 M 在被精确估计时取最大值。然而，往往难以估计也不必要精确估计。

综上所述，严格的马尔科夫边界要求我们进行条件独立性检测，这是一种困难的假设检验任务，而稳定学习可以求解相对容易的最小稳定变量集合。此外，对于常见的损失函数，马尔科夫边界并不是解决协变量迁移泛化的最小、最优的变量集合。（详见参考文献：https://arxiv.org/pdf/2111.02355.pdf）

04

浙江大学况琨：通过工具变量回归实现因果泛化

因果关系与稳定学习

如前文所述，现有的基于关联关系的机器学习算法存在一定的不稳定性。为此，研究者们提出了稳定预测/学习的框架，重点关注对未知的测试数据进行准确、稳定的预测。

现有的机器学习算法之所以不稳定，是因为这些算法是关联驱动的，而数据中存在大量的偏差，可能会导致模型提取出一些非因果关系的特征（虚假关联），从而导致模型不可解释、不稳定。为此，我们试图恢复出每个特征变量和标签 Y 之间的因果关系，从而找出因果特征。

2018 年，崔鹏老师、况琨老师等人提出了因果正则化技术，通过学习到全局权重使得变量之间相互独立，通过将该技术应用到逻辑回归、浅层深度网络等模型上，可以取得一定的性能提升。这种寻找因果关系的过程要求我们能够观测到所有的特征，然而有时一些因果特征是我们无法观测到的。

工具变量回归

在因果科学领域，研究者们以往通过工具变量（InstrumentalVariable）处理未观测到的变量。如上图所示，假设我们需要估计 T（干预）和 Y（结果）之间的因果效应，U 为未观测到的变量。工具变量 Z 必须满足以下三个条件：（1）Z 与 T 相关（2）Z 与 U 相互独立（3）Z 需要通过 T 影响 Y。

找到合适的工具变量 Z 后，我们可以通过二阶段最小二乘方法估计 T 与 Y 之间的因果效应。在第一阶段，我们根据 Z 回归 T，从而得到；在第二阶段，我们根据回归 Y，从而估计出T 与 Y 之间的因果函数。在上图左下角的例子中，黄色的曲线代表直接用神经网络回归的结果，红色的曲线代表引入工具变量后通过二阶段最小二乘回归得到的结果。实验结果表明，红色的曲线对原函数的拟合程度更好。

原始的工具变量回归方法以来于一些较强的线性假设。为此，近年来一些计算机研究人员提出了非线性的工具变量回归算法（例如，DeepIV、KernelIV 等）。从理论上说，在第一阶段，我们通过 Z 和 X 回归 T，得到；在第二阶段，我们通过和 X 回归 Y。此时，回归函数是非线性的。

然而，在实验中，DeepIV、KernelIV 等方法的效果并没有达到预期，这是因为第一阶段的回归为第二阶段引入了混淆偏差。在这里，我们考虑将混淆因子均衡引入工具变量回归中，从而解决这种混淆偏差问题。具体而言，在第一阶段的回归之后，我们会学习一种均衡的混淆因子表征，使得与无关。接着，在第二阶段，我们通过和回归 Y。

在使用原始的工具变量回归方法时，我们往往需要预先定义一个工具变量。在论文「Auto IV：Counterfactual Prediction viaAutomatic Instrumental Variable Decomposition」中，况琨博士等人在给定干预 T，输出结果 Y，观测到的混淆因子 X，未观测到的混淆因子 U 的情况下，从观测到的混淆因子 X 中解耦出工具变量。尽管分理出的工具变量可能不具备明确的物理意义，但是它满足前文提到的工具变量所需要满足的三个属性。这样生成的工具变量可以帮助我们估计 T 和 Y 之间的关系。具体而言，我们通过互信息判断特征之间的条件独立性，以及表征学习实现解耦操作。

通过工具变量回归实现因果泛化

工具变量回归可以被用于域泛化、不变因果预测、因果迁移学习等任务中。以域泛化为例，给定来自不同观测环境中的数据，该任务旨在利用给定的 X 预测 Y。我们希望从多个数据域（环境）中学习不变性，使得预测模型对于所有可能的环境都鲁棒。

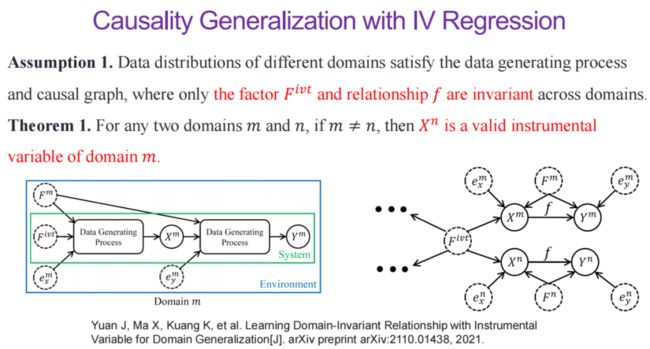
在通过工具变量回归解决域泛化问题时，首先，我们通过因果图刻画各个域中数据的生成过程（DGP）。对于域 m，在生成样本数据 X时，除了样本的域不变性特征之外，还可能受到域特定特征（例如，光照、天气）的影响；在为样本打标签时，标注者除了会考虑图片样本特征，也会受到域特定特征的影响。

在这里，我们假设各个域间具有不变性特征，且 X 和 Y 之间的关系是不变的。纵观多个域中的数据生成过程，域 n 中的样本恰好是域 m 中样本的工具变量，满足上述工具变量的三个特性。因此，我们可以通过工具变量回归的方式学习 X 和Ｙ 之间的因果效应 f。

在具体的求解过程中，我们首先通过工具变量回归，即估计。接着，我们利用近似出的和学习不变性函数。值得注意的是，在通过工具变量进行域泛化时，我们只需要一个域中的标签Y，以及其它域中的无标签数据 X。