Lytain2022

HLS：卷积神经网络LeNet5的实现与测试

一、引言

1、开发环境。

Windows10、Vivado2018.2、Vivado HLS与Xilinx SDK。

2、LeNet5概述。

1994年，CNN网络，手写字符识别与分类，确立了CNN结构，适合入门。

LeNet5共分为7层：

C1，卷积层
S2，池化层
C3，卷积层
S4，池化层
C5，卷积层
F6，全连接层
OUTPUT，全连接层

二、LeNet5的学习

LeNet5每层结构内容的学习。

1°输入层INPUT。

一般不视为网络层次结构之一。输入层为尺寸32x32的图片，由于MNIST数据集也是32x32的。因此不用做额外的尺寸调整操作。否则，需要根据训练的数据集输入不同，需要做尺寸的变换。

2、卷积层C1。

本质就是输入图片与卷积核做点积（数量积）。下图为一个5x5输入图片与3x3卷积核做卷积的例子。

通过卷积操作输出的一张3x3的新图称为特征图feature map。卷积意义在于利用不同的卷积核扫描图像，来提取图像不同的特征，比如[[-1 -1 -1],[ 2 2 2],[-1 -1 -1]]便可以提取出水平方向的边缘。

参数理解：

1°输入：32x32的图像。

2°卷积核种类：6种，故C1层理论上，可以提取出输入图像种6种不同的特征。

3°卷积核大小：5x5的大小。

4°输出特征图数量：6张输出特征图feature map，这是由于每个不同的卷积核分别与输入图像进行卷积运算，因此总共可得到6份输出。

5°输出特征图大小：28x28大小。由于没有进行Padding，feature map的大小为“输入图像 - 卷积核 + 1”，即“32 - 5 + 1 = 28”。

6°神经元数量：28×28×6。在神经网络的学习中，可以知道神经元其实就是一个"数"。而卷积层C1是由6张特征图组成的，每张特征图中包含28×28个像素，一个像素其实就是一个0~255之间的数(表示灰度值)，对应着一个神经元。因此共有28×28×6=4704个神经元。

7°可训练参数：(5×5+1)×6。首先，每个卷积核是一个5×5的矩阵，矩阵里的每个数都是要“通过训练”得到的。此外，在实际卷积运算后还要加上一个偏置(bias)，因此每个卷积核需要训练5×5+1个参数，6个卷积核共需要训练(5×5+1)×6=156个参数。

8°连接数：28×28×(5×5+1)×6。卷积层的每个特征图的各像素都与其对应的卷积核的各参数间有连接。一共有6张这样的“特征图——卷积核对”，每个“特征图——卷积核”对包含28×28×(5×5+1)×6个连接，因此共有28×28×(5×5+1)×6=122304个连接。需要注意的是，由于权值共享机制的存在，我们只需要训练156个参数。

3、池化层S2。

在这里，池化(pooling)是进行下采样(downsampling)操作，即对图像进行压缩。一般而言，池化往往在卷积层后面，可以降低卷积层输出的特征向量，改善过拟合的现象。

参数理解：

1°输入：28×28的特征图（6张）。

2°采样区域：2x2。在这里，采样方式为4个输入相加，乘以一个可训练参数，再加上一个可训练偏置，并将结果通过sigmoid函数。

3°输出特征图大小：14×14大小。具体计算可以看其他文章。

4°输出特征图数量：6张。

5°神经元数量：14×14×6。计算方法同上一节，每张特征图有14×14个像素，共6张，因此有14×14×6=1176个神经元。

6°可训练参数：2×6。对于每张特征图，只有两个参数需要确定：用于相乘的“可训练参数”与“可训练偏置”，共6张特征图，因此要训练6×2=12个参数。

7°连接数：14×14×6×(2×2+1)。池化层的每个特征图的各像素都与2×2采样区域以及1个偏置有连接。因此共有14×14×6×(2×2+1)=5880个连接。

4、卷积层C3。

1°输入：14x14大小的6张特征图。

2°卷积核种类：16个。因此卷积层C3能够提取出更多细微的特征。

3°卷积核大小：5x5的大小。

4°输出特征图数量：16张。
在卷积层C1中，卷积核有6种，而输入图像只有1张，因此只需要将6个卷积核分别对1张图像进行卷积操作，最后得到6张特征图。那么输入6张图像的话应该怎么处理呢？
在这里，采用的方法是"每个卷积核对多张特征图"进行处理，例如，编号为0的卷积核处理编号为0、1、2的特征图，编号为15的卷积核处理编号为0、1、2、3、4、5的特征图…具体的对应规则如下（其实就是输入多张的feature_in，在之前关于HLS的channel的补充有提到）：

横轴为编号0 ~ 15的16个卷积核，纵轴为编号为0 ~ 5的6张输入特征图。一种方便的记忆方法是前6个卷积核处理三张连续的特征图(对应第一个红框)，之后6个卷积核处理四张连续的特征图(对应第二个红框)，之后3个卷积核处理四张两两连续的特征图(对应第三个红框)，最后1个卷积核处理全部六张特征图(对应最后一个红框)。

5°输出特征图大小：10x10的大小。输出特征图的边长为14-5+1=10。

6°可训练参数：1516。以第一个红框为例。首先，每个卷积核包含5×5个可训练的参数。而在这里每个卷积核需要与3张特征图相连，最后还要加上1个偏置，因此需要训练3×5×5+1个参数。第一个红框内有6个这样的卷积核，因此共需要训练6×(3×5×5+1)个参数。同理，对于第二个红框，其共需要训练6×(4×5×5+1)个参数；对于第三个红框，其共需要训练3×(4×5×5+1)个参数；对于第四个红框，其共需要训练1×(6×5×5+1)个参数。总计可训练6×(3×5×5+1)+6×(4×5×5+1)+3×(4×5×5+1)+1×(6×5×5+1)=1516个参数。

7°连接数：10×10×1516。卷积层的每个特征图的各像素都与其对应的卷积核的各参数间有连接。因此共有10×10×1516=151600个连接。卷积层C3采用这种“卷积核——特征图”组合方式的好处有：减少参数、有利于提取多种组合特征（因为组合方式并不对称）。

5、池化层S4。

1°输入：10x10的16张特征图。

2°采样区域：2x2。在这里，采样方式为4个输入相加，乘以一个可训练参数，再加上一个可训练偏置，并将结果通过sigmoid函数。

3°输出特征图大小：5x5的大小。

4°输出特征图数量：输出16张的特征图。

5°神经元数量：5×5×16。每张特征图有5×5个像素，共16张，因此有5×5×16=400个神经元。

6°可训练参数：2x16。对于每张特征图，只有两个参数需要确定：用于相乘的“可训练参数”与“可训练偏置”，共16张特征图，因此要训练2x16=32个参数。

7°连接数：5×5×16×(2×2+1)。池化层的每个特征图的各像素都与2×2采样区域以及1个偏置有连接。因此共有5×5×16×(2×2+1)=2000个连接。

6、卷积层C5。

1°输入：5x5的16张特征图。

2°卷积核种类：120个。

3°卷积核大小：5×5。

4°输出：120维向量。

5°算法：每个卷积核与16张特征图做卷积（这样，一个卷积核会有16个channel，与16张feature_in进行卷积，会得到16张feature_map的预处理结果，再将所有结果求和，得到一个卷积核的feature_map），得到的结果求和，再加上一个偏置，结果通过sigmoid函数输出。

6°可训练参数：(5x5x16+1)x120。对于每个卷积核，其要与16张特征图的每个像素以及偏置相连，共120个卷积核，因此要训练的参数为(5x5x16+1)x120=48120。

7、全连接层F6。

1°输入：120维向量。

2°算法：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。F6层有84个结点，本质上对应一张7×12的比特图。实际上，ASCII码就可以用一张7×12的比特图来表示，每个像素若为-1则表示白色，1表示黑色。该全连接层的设计也是利用了这一思想。

3°输出：84维向量。

4°可训练参数：84×（120+1）。对于F6层的每个结点，其值是由输入向量与权重向量做点积得到的，而由于权重向量与输入向量的维度相同，因此权重向量也是120维的，需要训练120个参数，加上偏置，每个结点需要训练121个参数。一共有84个结点，因此需要训练84×121=10164个参数。

8、全连接层OUTPUT。

1°输入：84维向量。本质上是一张7×12的比特图，表示经过我们多层处理最终得到的一张"数字图像"。

2°输出：10维向量。OUTPUT层共有10个结点y0、y1、…、y9，分别对应着数字0到9。采用径向基函数(RBF)的连接方式，计算方式为：
$y_i=\sum_{j=0}^{83}{\left( x_j-w_{ij} \right)}^2$

其中，wij的值由数字i的比特图编码(即之前展示的ASCII码比特图编码)确定。如果结点yi的计算结果最小，则数字识别的结果为数字i。本质上是比较“我们处理得到的数字比特图”与“真实比特图”之间的相似度。

9、小结。

三、数学知识补充

1、如何使用C语言计算exp(x)。

在C语言中，通过极限的方式来计算e的x次方。具体计算公式如下：

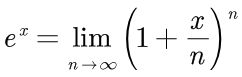
也就是说，n的值越大，那么e的x次方的结果更加的准确。比如n=256=2^8的话，可以通过下面的方式，先把括号内的式子表示出来，再将这个式子作256次方的处理，既可以计算出e的x次方的值。代码如下：

Double exp(double x)
{
 	x = 1.0 + x/256;
	x *= x; x *= x; x *= x; x *= x;
	x *= x; x *= x; x *= x; x *= x;
	return x;
}

本设计中的代码使用了n为1024的处理，即2的10次方，即作10次的x *= x操作。具体代码如下。

float expf(float x) {
	x = 1.0 + x / 1024;
	x *= x; x *= x; x *= x; x *= x; x *= x; 
	x *= x; x *= x; x *= x; x *= x; x *= x; 
	return x;
}

这种算法的优点，在于避免了指数运算，大大提高了运算速度。如果直接运算，则需要1024次乘法。该算法只需要10次乘法即可实现。

2、平均池化。

具体代码如下。

// 输入四个图像数据，四个数据相加，求平均值得到一个结果。
float AvgPool_2x2(float input[4]){
	float res = 0;
	int i;
	for(i = 0; i < 4 ; i++){
		res += input[i];
	}
	res /= 4;
	return res;
}

3、sigmoid函数的实现。

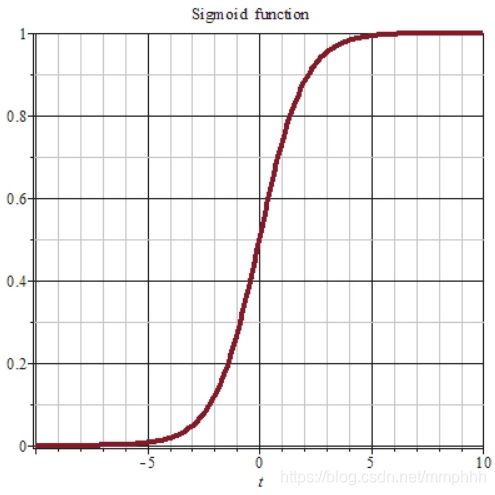
函数的表达式如下，波形图如上。

具体代码如下。

float sigmoid(float x)
{
    return (1 / (1 + expf(-x)));
}

4、softmax函数，又称归一化指数函数。（还需要再继续学习，挖坑）

按照字面意思，softmax即是将一个k维向量z，映射到另一个k维空间中，这种映射函数就是softmax。之所以要用softmax来映射一遍，是因为softmax可以将向量z的每个维度的取值均压缩至(0,1)之间。这就是softmax的本质，也是softmax函数的初衷

softmax函数的表达式就显而易见了：分母是所有k维向量z所有维度的自然底数e指数之和，分子是待求维度的自然底数e的指数，如下所示：

$softmax(z)_j = \dfrac{e^{z_j}}{\sum_{k=1}^{K}e^{z_k}}$

其中，左边式子指的是k维向量z经过softmax函数映射后的第j维的取值。

softmax在机器学习或深度学习中，更多的是以“多项逻辑回归”而存在的，用来计算样本向量x^(i)属于某个类别的概率分布。其中，属于第j个类别的概率为：

$P(y^{(i)}|x^{(i)};\Theta) = \dfrac{e^{\Theta^{T}X^{(i)}_j}}{\sum_{k=1}^{K} e^{\Theta^{T}X^{(i)}_k}}$

Softmax名字由来：不同于普通的max函数，max函数只输出最大的那个值，而Softmax则确保较小的值也有较小的概率，不会被直接舍弃掉，是一个比较“Soft”的“max”，这个“soft”是对比合页损失的“hard”而来的。

四、HLS代码设计

1、5x5kernel基本运算单元。

代码如下，利用这个最小的卷积基本运算单元，可以完成一次5x5数据和5x5的kernel的点积运算。

float Conv_5x5(float input[25], float kernel[25]){
	int x,y;
	float result = 0;
	for(y = 0; y < 5; y++){
		for(x = 0; x < 5; x++){
			result += input[x+y*5] * kernel[x+y*5];
		}
	}
	return result;
}

2、卷积层C1的实现。

输入数据是一张32x32的图像，也就是1024个数据。这里使用的是浮点类型的输入数组（可以改成int型，因为输入的像素点也就整形）。

//kernel 5x5x6 = 25x6 = 150
void ConvLayer_1(float input[1024],float * C1_value,float * weights){
	int i_y,i_x,matrix_y,matrix_x;  // 循环变量和中间变量
	int k_num,mat_i = 0;            // 不同kernel的计数变量
	
	// 定义循环名称为top_loop，方便优化
	// k_num为不同卷积核的循环变量，第一层有6个不同的卷积核，自然循环6次产生6张feature map
	top_loop:for(int k_num = 0; k_num < 6; k_num+=1){
		// 卷积核的权重数据变量matrix_2，用来存放kernel数据的
		// 第一层C1有6个不同的kernel，利用外层的top_loop可以完成对这些不同的kernel进行赋值
		// 5x5的kernel有25个变量，循环25次来放
		float matrix_2[25];
		for(mat_i = 0;mat_i<25;mat_i++){
			matrix_2[mat_i] = weights[mat_i + k_num*25];
		}
		// 一次卷积核操作，完成28*28的输出
		i_y_loop:for(i_y = 0; i_y < 28; i_y++){
			for(i_x = 0; i_x < 28; i_x++){
				float matrix[25];
				int pic_value_index = i_x + i_y * 32;
				// 通过25次循环，先把一个点乘运算所需的输入图像数据给弄出来，放到matrix中
				matrix_loop:for(matrix_y = 0; matrix_y <5; matrix_y++){
					caculate:for(matrix_x = 0; matrix_x <5; matrix_x++){
                        // 图片索引是0 ~ 24，这个也好理解，有25个数据
						int matrix_index = matrix_x + matrix_y * 5;
                        // 图片像素索引 0 ~ 1024。与matrix_x，matrix_y相关，x、y=32。
						int input_value_index = pic_value_index + matrix_x + matrix_y * 32;
						matrix[matrix_index] = input[input_value_index];
					}
				}
				// out_pic_index为输出数据的索引，从之前的学习，可以知道
				// C1后将输出28x28x6=4704个数据，而每个数据，可以由out_pic_index索引
				int out_pic_index = i_x + i_y * 28 + k_num * 784;
				// 通过最基本的卷积点乘单元，输入为图像数据和卷积核值。
				C1_value[out_pic_index] = Conv_5x5(matrix,matrix_2);
			}
		}
	}
}

3、池化层S2的实现。

第二层输入图像数据为28x28x6=4704，同时把输出的值用A2_value给传递出来。

void AvgpoolLayer_2(float input[4704],float *A2_value){
	int k_num,i_y,i_x,matrix_x,matrix_y;
	int count = 0;
	// 有6张feature map，需要循环6次
	for(k_num = 0; k_num < 6; k_num++){
		// 一张feature map大小为28x28，需要把每个数据给遍历了
		for(i_y = 0; i_y < 27; i_y+=2){
			for(i_x = 0;  i_x < 27; i_x+=2){
				float matrix[4];
				// 此时28x28x6某个图像数据的索引
				int index_now = i_x + i_y * 28 + k_num * 784;
				// 2x2的区域内，做一个平均池化
				for(matrix_y = 0; matrix_y < 2; matrix_y++){
					for(matrix_x = 0; matrix_x < 2; matrix_x++){
						// 将输出的索引转化为输入图像数据的索引，类似一个值映射变为四个值
						// 把四个索引里的值放到之前定义的matrix变量中，用于计算。
						int input_index = index_now + matrix_x + matrix_y * 28 ;
						matrix[matrix_x + matrix_y*2] = input[input_index];
					}
				}
				// 将28x28个数据遍历完，计算四个产生的一个结果，具体是四个数据相加
				// 加后乘上一个1/4，为均值，同时偏置设为了0，最后将结果通入sigmoid函数
				// 为了方便，这里并没有对池化中相加后乘的那个均值数做训练，且偏置也没有训练
				A2_value[count] = sigmoid(AvgPool_2x2(matrix));
				count++;  // 计数变量增加，来完成28x28遍历下的所有输出
			}
		}
	}
}

4、卷积层C3的实现。

输入数据为14x14x6的图像数据，即1176。剩下的就是卷积操作而已，和之前的C1层是一样的，只不过参数有些不同。

//kernel 5x5x6x16 = 25x6x16 =2400
void ConvLayer_3(float input[1176],float *C3_value,float * weights){
	int k_num,nk_num,i_y,i_x,matrix_x,matrix_y;
	int mat_i;
    for(nk_num = 0; nk_num < 16; nk_num++){
		for(i_y = 0; i_y < 10; i_y++){
			for(i_x = 0; i_x < 10; i_x++){
				float res = 0;
				float res_total_6 = 0;
				float matrix[25];
				int index_now = i_x + i_y * 10 + nk_num * 100;
				for(k_num = 0; k_num < 6; k_num++){
					float matrix_2[25];
					for(mat_i = 0;mat_i<25;mat_i++){
						int weights_index = mat_i + k_num*25 + (nk_num+1)*150;
						matrix_2[mat_i] = weights[weights_index];
					}
					for(matrix_y = 0; matrix_y <5; matrix_y++){
						for(matrix_x = 0; matrix_x <5; matrix_x++){
							int matrix_index = matrix_x + matrix_y * 5;
							int input_value_index = index_now + matrix_x + matrix_y * 14;
							matrix[matrix_index] = input[input_value_index];
						}
					}
					res_total_6 += Conv_5x5(matrix,matrix_2);
				}
				C3_value[index_now] = res_total_6;
			}
		}
	}
}

5、池化层S4的实现。

操作和之前的S2是相似的，只不过参数不同罢了。

void AvgpoolLayer_4(float input[1600],float *A4_value){
	int k_num,i_y,i_x,matrix_x,matrix_y;
	int count = 0;
	for(k_num = 0; k_num < 16; k_num++){
		for(i_y = 0; i_y < 10; i_y+=2){
			for(i_x = 0;  i_x < 10; i_x+=2){
				float matrix[4];
				int index_now = i_x + i_y * 10 + k_num * 100;
				for(matrix_y = 0; matrix_y < 2; matrix_y++){
					for(matrix_x = 0; matrix_x < 2; matrix_x++){
						int input_index = index_now + matrix_x + matrix_y * 10 ;
						matrix[matrix_x + matrix_y*2] = input[input_index];
					}
				}
				A4_value[count] = sigmoid(AvgPool_2x2(matrix));
				count++;
			}
		}
	}
}

6、全连接层

直接使用三层全连接层，来代替最后的卷积层C6和全连接层F6，因为数据量也不是很大了。

//kernel 400x120 = 48000
void FullyConnLayer_5(float input[400],float *F5_value,float * weights){
	int i_y,i_x;
	for(i_y = 0; i_y < 120; i_y++){
		float res = 0;
		for(i_x = 0;  i_x < 400; i_x++){
			int index = i_x + i_y * 400;
			res += input[i_x] * weights[index + 2550];
		}
		F5_value[i_y] = res;
	}
}
//kernel 84x120 = 10080
void FullyConnLayer_6(float input[120],float *F6_value,float * weights){
	int i_y,i_x;
	for(i_y = 0; i_y < 84; i_y++){
		float res = 0;
		for(i_x = 0;  i_x < 120; i_x++){
			int index = i_x + i_y * 120;
			res += input[i_x] * weights[index + 50550];
		}
		F6_value[i_y] = res;
	}
}
//kernel 10x120 = 1200
void FullyConnLayer_7(float input[84],float *F6_value,float * weights){
	int i_y,i_x;
	for(i_y = 0; i_y < 10; i_y++){
		float res = 0;
		for(i_x = 0;  i_x < 84; i_x++){
			int index = i_x + i_y * 84;
			res += input[i_x] * weights[index + 60630];
		}
		F6_value[i_y] = res;
	}
}

7、Softmax的实现。

输出判断的结果和对应的概率。

int Softmax_1_8(float input[10],float *probability,float *res){
	int index;
	float sum = 0;
	for(index = 0; index < 10; index++ ){
		probability[index] = expf(input[index]/1000);
		sum += probability[index];
	}
	int max_index = 0;
	for(index = 0; index < 10; index++ ){
			res[index] = probability[index]/sum;
			float res1 = res[index];
			float res2 = res[max_index];
			if(res1 > res2){
				max_index = index;
			}
	}
	return max_index;
}

8、LeNet的实现。

权重部分的读取，需要重新设计。

void LetNet(volatile float *addrMaster,int* r){
#pragma HLS INTERFACE m_axi depth=62855 port=addrMaster offset=slave bundle=MASTER_BUS
#pragma HLS INTERFACE s_axilite port=r bundle=CRTL_BUS
#pragma HLS INTERFACE s_axilite port=return bundle=CRTL_BUS

	// 32x32 iamge
	float photo[1024];
	//layer1 weights  5x5x6 = 25x6 = 150
	//layer3 weights  5x5x6x16 = 25x6x16 =2400
	//layer5 weights 400x120 = 48000
	//layer6 weights 84x120 = 10080
	//layer7 weights 10x120 = 1200
	float data[62855];
	//The output of each layer
	float C1_value[4704];
	float A2_value[1176];
	float C3_value[1600];
	float A4_value[400];
	float F5_value[120];
	float F6_value[84];
	float F7_value[10];

	float probability[10];
	float res[10];
	int loop1_i;
	//memory copy from BRAM to FPGA's RAM, 从addrMaster地址开始，复制62855个浮点型的数据到data数组中去。
	memcpy(data,(const float*)addrMaster,62855*sizeof(float));
	//get the image data, 32x32=1024 datas
	for(loop1_i = 0; loop1_i<1024; loop1_i++){
		photo[loop1_i] = data[loop1_i+61830];  // 前61830放的都是权重数据，后面才是图片数据
	}
	//calulation of each layer
	ConvLayer_1(photo,C1_value,data);
	AvgpoolLayer_2(C1_value,A2_value);
	ConvLayer_3(A2_value,C3_value,data);
	AvgpoolLayer_4(C3_value,A4_value);
	FullyConnLayer_5(A4_value,F5_value,data);
	FullyConnLayer_6(F5_value,F6_value,data);
	FullyConnLayer_7(F6_value,F7_value,data);
	*r = Softmax_1_8(F7_value,probability,res);
}

9、TestBench的设计。

关于权重和输入图像数据部分，需要重新设计。

#include "LeNet.h"
#include "stdlib.h"
#include 
using namespace std;
int main(){
	srand((unsigned)time(NULL));
	float weights[62855];
	int r = 0;
//	float test[1024]={0},weights[51750]={0};
	for(long i_2 = 0; i_2<61830; i_2++){
		int r = rand()%1000;
		float r2 = (float)r/10000;
		weights[i_2] = r2;
	}
	for(int i_1 = 0; i_1<1024; i_1++){
		int r = rand()%255;
		weights[i_1+61830] = (float)r;
	}
	LetNet(weights,&r);
	std::cout<<"res:"<<r<<"\n";
	return 0;
}

五、仿真综合与优化

1、综合报告，没啥程序设计的问题。

六、Zynq平台搭建测试

这部分的工作，后面完成了模型训练再进行。

七、一些注意点

等填坑后补。

八、文献时间线与后续工作