跟着MindSpore一起学习深度概率

MindSpore开源将近半年，已经推出了蛮多的架构和模型算法创新特性，现有计划围绕模型及算法创新工作开设一个专栏，把过程中的思考/开发遇到的坑，和小伙伴们分享一下，欢迎各位来炮轰。主要包含下图所示几个系列，如果有新的想法，也会在该专栏下及时更新。

首先想和大家分享的是深度概率学习系列，名字中包含“深度”和“概率”两个词，其分别对应的就是深度学习和贝叶斯理论，也叫贝叶斯深度学习，深度概率学习简单来说主要是这两方面的融合。

l 深度学习和深度概率学习的关系

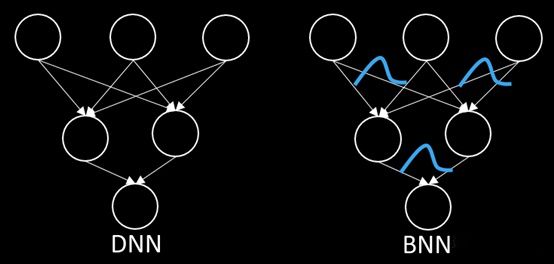
深度学习和深度概率学习有什么关系呢？一图告诉你它们的联系。

左边DNN代表的是深度神经网络，右边BNN代表的是贝叶斯神经网络，右图神经元连接的权重变成了分布的形式，一句话来说就是：将确定的权重值变成分布。大家可能想问了，权重变成分布有什么好处呢？

l 深度概率学习的优势

我们知道，深度学习模型具有强大的拟合能力，而贝叶斯理论具有很好的可解释能力，将两者结合，通过设置网络权重为分布、引入隐空间分布等，可以对分布进行采样前向传播，由此引入了不确定性，因此，增强了模型的鲁棒性和可解释性。

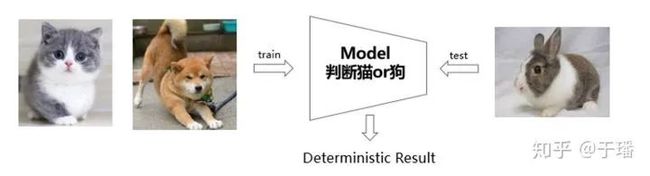
上面这段话可能比较难理解，简单来说，是在深度学习网络中加入了分布和采样等概率特性，引入了不确定性，即可以给出预测结果的置信度。这种能力是目前深度学习网络欠缺的，怎么理解不确定性呢？同样地一图告诉你。

给大家解释一下，假如深度学习网络训练的时候是猫狗数据集，在测试阶段传入了兔子的图片，此时模型的预测输出肯定是猫狗之一。但大家知道，这个显然是错的，而深度概率学习则会对预测结果给出置信度，如果这个值很高，那说明模型对预测结果是很不确定的。

l 深度概率学习的重要应用场景

深度概率学习在很多场景下都有应用，例如自动驾驶、目标检测/语义分割等应用场景。比如对自动驾驶时方向盘角度的预测，需要非常精确的估计，一旦估计错误会出现严重的后果，若具有很高的不确定性，应该交给驾驶员进行决策判断。

方向盘角度的预测

而目标检测/语义分割领域，可以对结果进行不确定性的估计，并可视化呈现出来，这样可以很清晰的知道这部分是由于数据还是模型带来的不确定性，增强模型的可解释性。

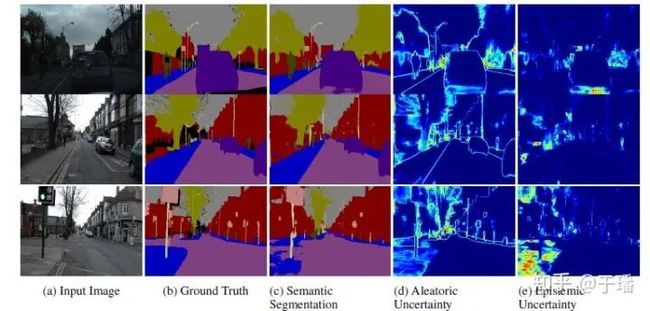
语义分割场景

从上图中的（d）和（e）可以知道，颜色亮暗代表不确定性的高低，那么我们可以很直观的知道哪部分分割效果不好，是由于什么引起的。

医疗图像诊断系统如果对某张图片不确定，也不可轻易给出预测结果，应该交给医生进一步诊断。

另外还包括主动学习、异常检测等应用场景，这个之后会专门写一篇文章，欢迎大家一起讨论。

l 业界经典的深度概率学习框架

大家了解了什么是深度概率学习后，接下来我们讲一下目前深度概率学习的框架。

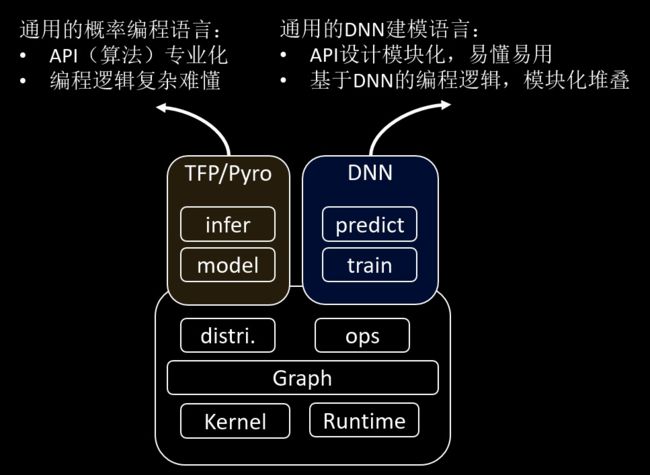
业界主流的框架主要为基于TensorFlow的TFP和基于PyTorch的Pyro，但这两个框架都存在着对深度学习用户不友好的问题，如下图所示，其API的设计比较专业化，编程逻辑也与我们熟悉的深度学习编程逻辑差异比较大，更适用于专业的概率学习人员。

那么，这里也引出了一个问题，为了让更多用户都能上手深度概率学习，应该设计出什么样的概率编程框架呢？

我们的想法和动机：

1)包含通用、专业的概率学习编程语言，适用于“专业”用户

2)使用开发深度学习模型的逻辑进行概率编程，“小白”用户轻松上手

3)深度学习模型与概率学习模型可模块化堆叠

4) 提供深度概率学习的工具箱，拓展贝叶斯应用功能

清华大学朱军老师团队在2017年开源了ZhuSuan框架--高效的贝叶斯深度学习库。MindSpore概率编程库基于ZhuSuan做了整合优化，开发出了概率学习模型和深度学习模型“无缝”融合的框架，旨在为用户提供完善的概率学习库，用于建立概率模型和应用贝叶斯推理。

MindSpore深度概率学习的目标是将深度学习和贝叶斯学习结合，并能面向不同的开发者。具体来说，对于专业的贝叶斯学习用户，提供概率采样、推理算法和模型构建库；另一方面，为不熟悉贝叶斯深度学习的用户提供了高级的API，从而不用更改深度学习编程逻辑，即可利用贝叶斯模型。

基于MindSpore的深度概率学习库地址：Gitee，Github

目前刚发出了第一个版本，后续会不断进行迭代和完善，也希望大家一起参与到社区来，文后附有链接。

深度概率学习系列将从以下几个方面来向大家介绍：

首先给大家介绍的是MindSpore深度概率学习库的特性，希望让大家对深度概率学习库有总体上的了解，后续会陆续更新介绍其功能模块。

l 深度概率特性

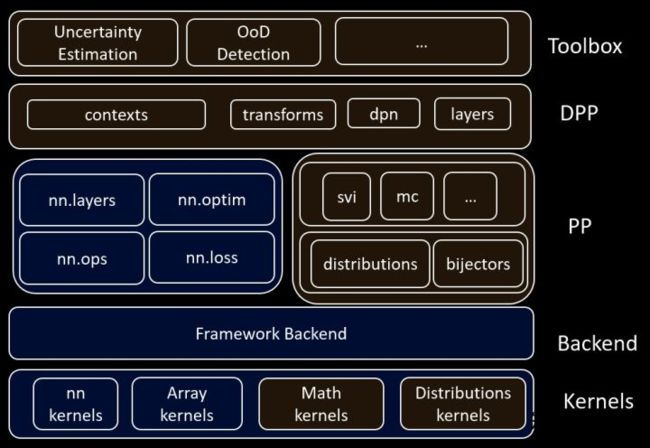
MindSpore深度概率学习库建立在MindSpore的基础之上，其支持高度灵活的模型表达和高性能的加速平台（包括Ascend和GPU），并具备训练过程静态执行和动态调试的能力，充分利用MindSpore的优势。其总体框架如下图所示：

看上去一头雾水，别着急，下面为大家自下向上进行讲解。

Kernels

内核模块主要指适用于不同平台的高性能内核，包括贝叶斯模型使用的Distribution kernels和Math kernels。我们知道，随机数生成器（RNG）在很多情况下都使用，为了生成随机数，MindSpore会针对不同分布的不同运算符，例如正态分布、均匀分布、伽玛分布、泊松分布等，这里大家是不是亲切多了，简单来说就是支持大部分的概率分布。另外，随机数生成器同时需要MindSpore前后端的支持。

Probabilistic Programming

概率编程是用于深度概率建模的工具，其目标是建立和训练深度概率网络，主要的两个部分是用于生成随机张量的统计分布类和概率推断算法。

Distributions and Bijectors

首先是统计分布类，其功能是支持分布/随机张量。分布/随机张量是随机变量/向量的数学概念的实现。与通常张量不同，分布/随机张量是没有确定性值的张量。相反，我们可以通过按照一定概率分布进行采样来获得随机张量的实现，或计算分布的统计性质。

随机分布的统计属性涵盖了概率统计中重要的统计属性，包括但不限于均值，方差/标准差，众数，分位数，概率分布函数（pdf），最大似然估计（log likelihood），累计分布函数（cdf）等。

而Bijector类可以用作从一个Distribution类实例到Transformed Distribution类实例的映射。举个例子，假如基本的Distribution是Normal分布，Bijector是Y=EXP(X)的映射，那么Transformed Distribution是EXP(Normal)，简单来说就是基本分布类到复杂分布类的映射，通过Bijector类，可以构建一些更复杂的概率分布。

Probabilistic Inference Algorithms

概率推断算法模块包含了最常见的两类推断算法：随机变分推断（SVI）和马尔科夫链蒙特卡洛算法（MCMC）。

在概率模型中，我们经常需要根据数据来近似复杂的概率分布，即对后验概率的计算，而这个概率往往很难计算。变分推断的基本思想是用隐藏变量来近似概率模型的后验分布，将求解数据的后验概率分布问题转化为优化问题。通过优化隐藏变量分布的参数来获取最接近的后验，通过Kullback-Leibler散度衡量，在变分推断中，极小化KL divergence的问题等价于最大化ELBO的问题。这里只是进行简单的概括，更多地可参考Variational Inference: A Review for Statisticians这篇论文，对变分推断总结的非常好。

另一种推断算法是马尔可夫链蒙特卡罗（MCMC）。在统计中，马尔可夫链蒙特卡洛（MCMC）方法包括一类用于从概率分布中采样的算法。通过构建具有所需分布作为其平衡分布的马尔可夫链，可以通过记录链中的状态来获得所需分布的样本。MCMC是概率编程中的重要模块，可支持包括数据生成和推断在内的模型功能。关于MCMC的详细介绍，@Eureka的文章写得很清楚，大家可以参考里面的解释：马尔可夫链蒙特卡罗算法（MCMC）

Deep Probabilistic Programming

该模块旨在提供可组合的概率编程模块，包括Layers、Transform和Deep Probabilistic Network等，这部分也是希望可以用开发深度学习模型的逻辑来构造深度概率模型。

Layers

贝叶斯神经网络（BNN）是由概率模型和神经网络组成的基本模型，文章刚开始画的就是典型的贝叶斯神经网络，BNN以分布形式表示神经网络的权重，该模块提供了可组合成BNN的Layers。不同于深度神经网络层，这些层在权重和偏置上分配分布，并在输出上产生不确定性，BNN和DNN的区别在于BNN需要计算参数层的后验值，并且BNN的每层layer都需要计算KL loss，所以在训练阶段有所不同。该模块提供的功能是使得用户可以像构建DNN网络一样构建BNN网络。大家如果想实践一下，具体的使用示例可以参考：Bayesian LeNet

Transform

该模块提供了DNN一键转BNN网络，我们知道对于不熟悉概率学习的用户而言，构建和训练概率神经网络并不友好，所以为这些用户提供了高级的API用来构建贝叶斯神经网络。除了支持模型级别的转换，还支持层级的转换。通过该API，用户可以很方便地构建贝叶斯神经网络，上手十分容易。

欢迎大家尝鲜，使用示例：Transform DNN model to BNN

Deep Probabilitic Network

Deep Probabilitic Network意思就是深度概率网络，我们希望能提供一些典型的概率网络模块供用户使用。

这其中，Variational AutoEncoder (VAE)是经典的应用了变分推断的深度概率模型，用来学习潜在变量的表示，通过该模型，不仅可以压缩输入数据，还可以生成该类型的新图像。我们将构建网络以产生潜在表征向量，这些潜在表征向量的遵循正态分布，通过变分推断算法来最大化ELBO，使得潜在变量和标准正态分布的差异尽可能的小。在尝试生成新数据时，只需简单地从分布中采样一些值，然后将它们传递给解码器，解码器将返回一些新数据，并且新生成的数据具有多样性。

使用该模块来构造变分自编码器（VAE）进行推理尤为简单。用户只需要自定义编码器和解码器（DNN模型），调用VAE或CVAE接口形成其派生网络，然后调用ELBO接口进行优化，最后使用SVI接口进行变分推理。这样做的好处是，不熟悉变分推理的开发者可以像构建DNN模型一样来构建概率模型，而熟悉的开发者可以调用这些接口来构建更为复杂的概率模型。具体的使用示例同样大家可以参考：Variational Auto-Encoder

Toolbox

在本篇开头有提到，贝叶斯神经网络的优势之一就是可以获取不确定性，MindSpore深度概率学习库在上层提供了不确定性估计的工具箱，用户可以很方便地使用该工具箱计算不确定性。

再次说一下什么是不确定性：不确定性意味着深度学习模型不知道什么。目前，大多数深度学习算法只能给出高置信度的预测结果，而不能判断预测结果的确定性，不确定性主要有两种类型：偶然不确定性和认知不确定性。

偶然不确定性（Aleatoric Uncertainty）：

描述数据中的内在噪声，即无法避免的误差，这个现象不能通过增加采样数据来削弱，也叫做数据不确定性。

认知不确定性（Epistemic Uncertainty）：

模型自身对输入数据的估计可能因为训练不佳、训练数据不够等原因而不准确，可以通过增加训练数据等方式来缓解，也叫做模型不确定性。

提供的不确定性估计工具箱支持主流的深度学习模型，目前主要包括回归和分类任务。在推理阶段，用户只需传入训练好的模型和训练数据集，指定任务和待估计的样本，即可方便地获取偶然不确定性和认知不确定性，在不确定性信息的基础上，用户可以更好地理解模型和数据集。不确定性估计工具箱的使用可参考：Toolbox of Uncertainty Estimation

---

特别感谢清华大学的ZhuSuan团队Jiaxin Shi（石佳欣）和 Jianfei Chen（陈键飞）等人对MindSpore深度概率编程社区的贡献，希望更多的人能参与进来一起完善。

这里也列出几个问题想和大家一起探讨：

1. 为了让更多用户都能上手深度概率学习，应该设计出什么样的概率编程框架呢？

2. 深度概率学习具有更好的鲁棒性和不确定性，是否还有其他的应用场景呢，及普及的局限性在哪？

3. 不确定性是现在贝叶斯网络的优势之一，那么我们更多地能用不确定性来做什么？

本篇文章就到这里啦，欢迎大家批评指正。下一篇文章我们会详细地介绍概率推断算法和概率模型，包括模块功能、设计的原理和使用方式等。