OpenGL超级宝典笔记(零)数学基础与基础变换
这部分与(一)的不同是这部分只注意使用价值,不搞矩阵怎么运算那些虚的,而且结合OpenGL来讲。
声明:摘抄,翻译,感悟自http://www.songho.ca/opengl/gl_transform.html#modelview
主要流程
基础数学知识
- 别理太多,反正转换矩阵总是在坐标或者向量的前面,公式一直都是
C o o r d d s t = M t r a n s f o r m ∗ C o o r d o r i Coord_{dst} = M_{transform} * Coord_{ori} Coorddst=Mtransform∗Coordori
如果要连续做两个变换,那么慢做转换那个矩阵反而要在前面。
摄像机以及物体变换
第一个要素是物体本身的世界坐标。
在第一个步骤会被转化到以摄像头为原点的坐标系中。由于在OpenGL中,摄像头的位置是固定在(0,0,0),并且朝向被固定在-z方向的,所以如果想要像在游戏引擎里面那种移动摄像头的操作的话,只能反过来转换物体的坐标。
移动和变换的叠加可以通过变换矩阵相乘来实现
∴ M m v = M v ∗ M m \therefore M_{mv} = M_v * M_m ∴Mmv=Mv∗Mm
M v M_v Mv在前面意味着先做世界坐标上物体的变换,再做相机的变换,这个很合理。如果反过来相机先变换,那么物体的变换就不是在世界坐标上了,会有奇妙的效果。
所以
C o o r d e y e = M m v ∗ C o o r d w o r l d Coord_{eye} = M_{mv} * Coord_{world} Coordeye=Mmv∗Coordworld
法向量的变换就不一样了,
不知道为啥但是就是这样:
n e y e = ( M m v − 1 ) T ∗ n w o r l d n_{eye} = (M_{mv}^{-1})^T * n_{world} neye=(Mmv−1)T∗nworld
取mv矩阵的逆矩阵的转置,乘以原法向量。所以vertex shader里面老是要的那个 M n o r m a l M_{normal} Mnormal(normalMatrix)其实就是这个又逆又转置的mv矩阵。
投影
C o o r d c l i p = M p r o j e c t i o n ∗ C o o r d e y e Coord_{clip} = M_{projection} * Coord_{eye} Coordclip=Mprojection∗Coordeye
标准化
NDC,其实就是除以 w w w。
C o o r d n d c = C o o r d p r o j e c t e d / w Coord_{ndc} = Coord_{projected} / w Coordndc=Coordprojected/w
屏幕剪裁
这里不管,OpenGL的插件做的。
矩阵
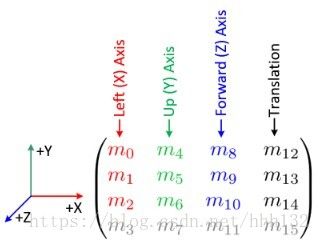
mv矩阵
其中, m 15 m_{15} m15是齐次因子。
( m 0 , m 1 , m 2 ) (m_{0}, m_{1}, m_{2}) (m0,m1,m2), ( m 4 , m 5 , m 6 ) (m_{4}, m_{5}, m_{6}) (m4,m5,m6), ( m 8 , m 9 , m 10 ) (m_{8}, m_{9}, m_{10}) (m8,m9,m10)分别代表xyz轴的变换。默认是(1,0,0), (0,1,0), (0,0,1)。旋转和缩放一般影响到这九个位。而位移是由 ( m 12 , m 13 , m 14 ) (m_{12}, m_{13}, m_{14}) (m12,m13,m14)控制的。如果不知道怎么得到最终的变换矩阵,那就旋转,缩放,位移一个一个乘起来。
投影
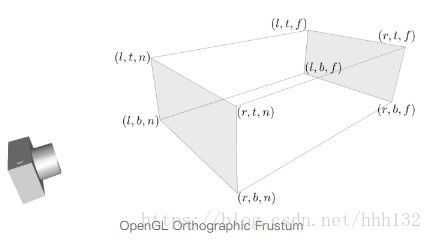
视锥体( f r u s t u m frustum frustum)投影(perspective)是常识了,相对应的ortho就是平行变换,一般用于2d的UI界面上。二者分别对应glPerpective()和glOrtho2D()。这部分变换把对应的东西投影到相机,并且做剪裁(far和near面)。

创建一个视锥体一般需要六个参数:left, right, bottom, top, near, far(上面图里的字母皆是这几个参数的头个字母)。
其中,near是近面和相机的距离,far是远面和相机的距离。
glPerpective()方法则只需要四个参数:一个Y方向FOV(field of view),也就是纵向的角度;一个aspect,长宽比;一个near;一个far。很容易猜到为啥少了两个参数,因为默认视锥体的高线穿过相机,整个视锥体是对称的。
为了视角剪裁,当然也需要near和far了(以前老以为不用),比far还远,比near且近者,当被屏蔽。