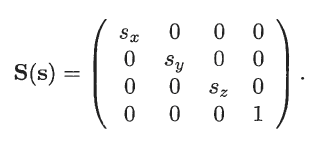【第一弹】探索矩阵转换、透视投影、OpenGL矩阵存储及操作特性、法线的应用以及GLFrame的使用
在进行为期一周的探索之前花了一个半月的时间学完《OpenGL超级宝典（第五版）》，基础篇和高级篇的缓冲区几个章节基本上都是实打实的很认真的在学，然后结合书上的例子应用，缓冲区后面的几个章节看起来表示压力相当大，也就没有很仔细的去看这些章节，所以这些章节就走马观花的看了个大概。看完这本书，我把OpenGL大致为分这几个模块来学习：
虽然锐爷觉得我的这种分法毫无逻辑可言，但是我感觉我要学通这个OpenGL大致按照这样的知识分块来学习更适合，也更快。
作为之前没怎么实际接触过3D开发，矩阵转换一直是我学习以来的一块硬伤，什么矩阵操作、矩阵变换、法线应用，还有顶点等等这些概念基本上大学学完了就全都忘掉了，仅仅在脑子里留下了一个很模糊的索引。所以我给我自己定了几个任务，矩阵转换、缓冲区、渲染流程这三块知识分别依次花一周的时间来学习消化。
这周我把矩阵转换这块基本上给搞明白了，顺带把OpenGL中涉及到顶点、法线、矩阵转换这些知识也全都理了一遍，我想这一块现在在还要我多加应用就能够很熟练的掌握了。现在把这些天我做的笔记整理出来，欢迎大家拍砖！
（周末奉献。。。。）
矩阵中关于行主元和列主元
>大学线性代数课本是用的行主元矩阵，OpenGL使用的是列主元矩阵。
行主元和列主元的意思是：在与顶点坐标相乘时，行主元为顶点坐标与矩阵的行相乘，列主元为顶点坐标与矩阵的列相乘。
>这里，我们有一样事情没有变，总是坚持：第一个矩阵的行与第二个矩阵的列的相应元素相乘之和作为新矩阵的对应元素。
可能列主元是蓝宝书第5版所要表达的真正意思。
OpenGL中矩阵本身的存储还是这样子的：
gl_Position = mvpMat * vVertex
常用的矩阵及附带一些顶点应用
#Q: 在矩阵进行缩放时可以进行正负缩放，那么正负缩放的具体意义是什么呢？是为了达到什么目的？
#Q: 另外设置正面的方法glFrontFace(GL_CCW) / glFrontFace(GL_CW)，这个对坐标转换有又多大关系？
#Q: 什么样的矩阵分别为旋转、缩放、平移矩阵？又如何将这三个矩阵结合为一个矩阵？这些矩阵如何对坐标进行转换的？
看完下面的关于矩阵这一章节内容的介绍，以上这三个问题都有答案了。以下这一部分知识是看的锐爷推荐的实时计算机图形学，以下列出的矩阵均为行主元。
>in fact alllinear transform for 3-element vectors, can be represented using a 3x3 matrix.
3元素向量的线性转换，都可以用3阶矩阵来表示。
线性转换需要达到的两个要求是：
f(x) + f(y) = f(x+y);
kf(x) = f(kx);
由此可知，旋转和缩放转换均为线性转换；而平移转换则为非线性转换，所以3元素向量的平移转换，不能用3阶矩阵来表示。
4阶矩阵能够表现一个线性转换和一个平移。
- 旋转
旋转矩阵：
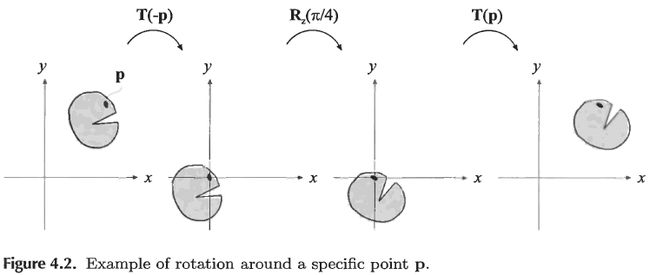
假如想围绕一个点p绕i轴旋转a角，那么就应该先平移-p距离T(-p)，在绕i轴旋转a角Ri(a)，然后再平移p距离T(p)；总的方程式就是：T(-p) x Ri(a)x T(p)。因为对物体进行旋转操作都是会绕经过原点的轴进行旋转，现在想围绕某一点p进行旋转，那么就得模拟将p点作为原点，所以需要先将其进行平移至原点，然后旋转，最后在平移回去。示意图如下：
#Q: 旋转矩阵为正交矩阵？
- 缩放
缩放矩阵：
在一个缩放矩阵上假如有一个缩放因子或者三个缩放因子为负数，那么这个矩阵就是反射矩阵；但假如有两个缩放因子为-1，那么将会使物体旋转一个PI的弧度角。
使用一个反射矩阵转换后，以逆时针顺序绘制的三角形图元将会得到一个顺时针顺序的绘制顶点，也就相当于在OpenGL中从GL_CCW顺序转换成了GL_CW，也即顺时针绘制的图元将是正面。（PS：我觉得反射矩阵这个用途还是相当有用的，即使用反射矩阵进行转换可使得以逆时针顺序绘制的图元顶点按照顺时针的顺序进行排列。reflection also called a mirror matrix）。
所以这也就不难理解在OpenGL蓝宝书中的例子：球体世界的场景反转，
modelViewMatrix.Scale(1.0f, -1.0f, 1.0f);
glFrontFace(GL_CW);
modelViewMatrix.Translate(0.0f, 4.0f, 1.0f);
objectBatch.Draw();
glFrontFace(GL_CCW);
首先通过缩放，此缩放矩阵中有一个缩放因子为负数，所以这个矩阵为反射矩阵，也即将场景图元的顶点排序从逆时针顺序还成了顺时针顺序，为了还保证这个面为正面，那么就得设置逆时针顺序排列的顶点的面为正面了。
假如缩放不是在x、y、z轴向上进行缩放，而是在其他的方向上进行缩放，那么就需要进行一个组合变换才能够达到要求。首先假设在其他方向上的缩放，这些方向轴相互垂直，而且对应的三个轴向分别为fx, fy, fz，那么先构造矩阵F：
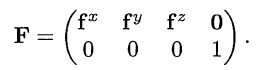
思路是将坐标系的轴向改为这三个轴向，然后进行缩放变换，最后再将坐标系的轴向还原回来。变换过程：
- shearing matrix
此类矩阵可以扭曲整个场景
矩阵x点
#TODO(continue):待补充
- Normal Transform
- 矩阵分解
通过检查矩阵行列式是否为负的来判断矩阵是否包含了反射矩阵；
要分离出旋转、缩放、shearing矩阵需要花费更多的努力；
平移矩阵就是最后一行一列！左上的3x3矩阵就是零矩阵。
缩放矩阵并不和平移分量连接，也就是说当给矩阵进行缩放向量时，缩放因子只是会乘以左上的3x3矩阵，而最后一行一列并不会被乘上缩放因子。#TODO(complete):待验证。
#result: 已验证，在GLFrame::GetMatrix和GetCamera方法中都是先计算好旋转矩阵然后再最后再在最后“一列”填上平移分量。
Thomas、Goldman和Shoemake实现了多种矩阵转换的算法。
- vertex blending
此项技术用于模拟手臂做曲轴运动等一些效果，这项技术有其他的名称：skinning, enveloping和skeleton-subspacedeform。
skeleton，貌似是骨骼运动，可能这章节讲的是骨骼运动模拟。
这个主要的是增加关节（Joint）。
>allow asingle vertex to be transformed by several different matrices.
允许一个顶点同时被多个不同的矩阵转换。
>One drawbackof basic vertex blending is that unwanted floding, twisting, andself-intersection can occur.
>One of thebest solutions is to use dual quaternions, as presented by Kavan et al.
参考资料：
vertex blending- Morphing
vertex morphing是指何意？用作什么呢？
即为顶点渐变：
>顶点渐变动画可以实现一些用骨骼动画比较不好实现的效果，比如人物表情动画，其基本思想就是通过建立一个基模型和几个目标模型，然后通过顶点插值从基模型过渡到目标模型，目标模型可以有任意多个。
顶点渐变的运算过程：
给出一个源模型，在给出几个目标模型，权重分量wi，通过公示4.58可以得出从元模型到目标模型的过渡模型，其中的过渡成都则是由权重wi来决定，若wi=1，则是完全过渡到目标模型。
这块资料整理的比较杂，比较乱，请见谅！投影矩阵的原理
>透视投影是3D固定流水线的重要组成部分，是将相机空间中的点从视锥体(frustum)变换到规则观察体(CanonicalView Volume)中，待裁剪完毕后进行透视除法的行为。在算法中它是通过透视矩阵乘法和透视除法两步完成的。
纠正了我原来的几个翻译问题：frustum,视锥体(非平截头体)，Canonical View Volume，规则观察体(CVV)。透视投影是通过透视矩阵乘法和透视除法两步完成的：
1) 用透视变换矩阵把顶点从视锥体中变换到裁剪空间的CVV中。
2) CVV裁剪完成后进行透视除法（一会进行解释）。
透视除法就是简单的将将向量都除以w分量，是向量的最后一个分量为1。
在透视矩阵乘法和透视除法之间的步骤是：CVV裁剪过程。
homogeneous coordinate：齐次坐标。
>齐次坐标能够用来明确区分向量和点。
齐次坐标用四个代数分量来表示，最后一个分量为0表示是向量，最后一个分量为1表示是点。
这句话很重要，因为在构造模型矩阵的时候，矩阵包含了以下几个信息：
>这4列中每一列都代表一个由4个元素组成的向量。
u 解释这些数字：
u 前3列的前3个元素只是方向向量，它们表示空间中x轴、y轴和z轴上的方向。
u 对于大多数应用来说，这3个向量相互之间总是成90°角，并且通常为单位长度（除非我们还应用了缩放或裁减）。这种情况下的数学属于叫做标准正交（向量为单位长度）或者正交（向量不是单位长度）。
u 矩阵的最后一行都为0，只有最后一个元素为1。
u 第4列向量包含变换后的坐标系原点的x、y和z值。
图例：
>空间中任何位置和任何想要的方向都可以有一个4x4矩阵唯一确定，并且如果用一个对象的所有向量乘以这个矩阵，那么我们就将整个对象变换到了控件中的给定位置和方向！
所以要分析一个矩阵起到什么作用基本上看这些内容就能够大致知道一些，就比如进行了平移、旋转、缩放等，都可以从中看出来。
普通坐标(Ordinary Coordinate)则是用三个代数分量来表示。
>如果把一个点从普通坐标变成齐次坐标，给x,y,z乘上同一个非零数w，然后增加第4个分量w；如果把一个齐次坐标转换成普通坐标，把前三个坐标同时除以第4个坐标，然后去掉第4个分量。
>基本思想是：给一个x属于[a, b]，找到y属于[c, d]，使得x与a的距离比上ab长度所得到的比例，等于y与c的距离比上cd长度所得到的比例，用数学表达式描述很容易理解：
>#Q: 透视投影会确定一个以Z为定值的一个投影平面吗？
我们在生成投影矩阵的时候只设置了远近参数，并没有设置投影平面。那这个远近参数是相对于谁而言的呢？难道是视点位置和视点方向？应该是的。
首先在我们设置相机位置后，利用相机变换后，顶点位置确实是相对相机位置移动了，
举例：定义相机变量
GLFrame cameraFrame;并定义一个顶点位置：
M3DVector4f vertex = {0.0f, 0.0f, 0.0f, 1.0f};当将相机向后移动1个单元：
cameraFrame.MoveForward(1.0f);那么相当于顶点向前移1个单元，将相机矩阵与顶点位置相乘后，顶点的坐标变为{0.0f, 0.0f, -1.0f,1.0f};
cameraFrame.GetCameraMatrix * vertex; //不能直接这样相乘类似，当相机向上或向左移动n个单元，那么进行相机变换后，顶点的坐标就对应的向下或向右移动n个单元。
由此可以推测透视投影所投向的平面也是相对相机位置的。
透视投影矩阵的推到步骤如下：
step1: 在进行投影变换之前会经过相机变换这一步骤，相机变换就是将顶点相对于相机位置进行移动，其移动的参考就是原始位置在(0.0f, 0.0f, 0.0f)位置的相机移动后到的另一个位置(x,y, z)。
step2: 继第一步之后就是选择一个平行于近裁剪平面的平面作为投影平面，一般选择近裁剪平面作为投影平面，视锥体的组成图如下所示：
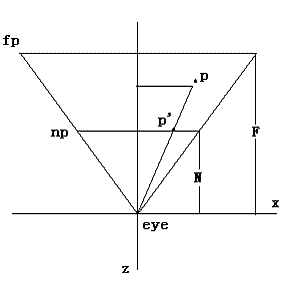
>视锥体由eye——眼睛位置，np——近裁剪平面，fp——远裁剪平面组成。N是眼睛到近裁剪平面的距离，F是眼睛到远裁剪平面的距离。
p点是经过相机变换之后的点，p’点是经过投影之后的点，根据相似三角形的性质，
这样投影后的p’点的坐标为：
从上可以看出，所有顶点的投影结果z的值都为-N。
step3: 既然已经找到了经相机变换后的初始顶点和投影后的顶点的关系，那么就可以计算出所有经过投影变换后的结果。但是最终我们要将这些点进行CVV裁剪过程。
CVV裁剪x,y,z的坐标大小区间均为[-1,1]之间，现在要将投影转换后的顶点的x,y分别从区间[left, right]和区间[bottom, top]能够通过线性插值映射出区间[-1, y的]x’,y’。那这里Z的值怎么办呢？至于在此篇博客中讲到的要在Z轴方向上也构造一个CVV，这个我就不太能理解了，因为所有的顶点在经过投影变换后Z的值是一个定值，也就是说在Z方向上我不需要对它进行裁剪，那一般来说我为了简化处理，我就直接在矩阵中让z方向上的值为0即可。此处不理解。
这里对正交投影和透视投影都不算很理解，但是里面基本的一些操作步骤和原理也知道了个大概，这个还是以后在应用开发中在融合理解吧，现在理解到这个程度也差不多了。。。
OpenGL超级宝典第5版提到一个在屏幕空间进行2D绘制的技巧：
>在屏幕空间中进行2D绘制时，普遍的做法是创建一个与屏幕大小相匹配的正投影矩阵。但是将原点(0, 0)设置在了左下角而不是左上角，这样就能保证绘制坐标都干净整齐地落在笛卡尔坐标系第一象限中了。
对这个投影矩阵的设置代码示例如下：
M3DMatrix44f mScreenSpace;
m3dMakeOrthographicMatrix(mScreenSpace, 0.0f, 800.0f, 0.0f, 600.0f, -1.0f, 1.0f);
投影矩阵暂时就说到这里吧，以后在做应用的时候如果有一些心得体会再讲出来。。。现在的理解层面也就只到这里了。