Leetcode刷题:热题HOT100-Medium篇-Python多算法实现(1-10题更新完毕)
系列文章目录
Leetcode刷题:热题HOT100-EASY篇-Python多算法实现(完结-共21题)
Leetcode刷题:热题HOT100-Medium篇-Python多算法实现(完结-1~10题)
Leetcode刷题:热题HOT100-Medium篇-Python多算法实现(完结-11~20题)
文章目录
- 系列文章目录
- 前言
- 1.两数相加(链表)
-
- 1.1 题目描述
- 1.2 核心思路
- 1.3 代码
- 2.无重复字符的最长子串(滑动窗口+哈希表)
-
- 2.1 题目描述
- 2.2 核心思路
- 2.3 代码
- 3.最长回文子串(动态规划)*
-
- 3.1 题目描述
- 3.2 核心思路
- 3.3 代码
- 4.盛最多水的容器(双指针)*
-
- 4.1 题目描述
- 4.2 核心思路
- 4.3 代码
- 5.电话号码的字母组合(递归,回溯)
-
- 5.1 题目描述
- 5.2 核心思路【还可以采用队列,后续补充】
- 5.3 代码
- 6.删除链表的倒数第N个结点(链表)
-
- 6.1 题目描述
- 6.2 核心思路
- 6.3 代码
- 7.括号生成(回溯,递归)
-
- 7.1 题目描述
- 7.2 核心思路
- 7.3 代码
- 8.组合总和(回溯,递归)
-
- 8.1 题目描述
- 8.2 核心思路
- 8.3 代码
- 9.全排列(回溯)
-
- 9.1 题目描述
- 9.2 核心思路
- 9.3 代码
- 10.子集(回溯)
-
- 10.1 题目描述
- 10.2 核心思路
- 10.3 代码
前言
记录LeetCode 热题 HOT 100的Medium题目题解,采用python实现。
1.两数相加(链表)
1.1 题目描述
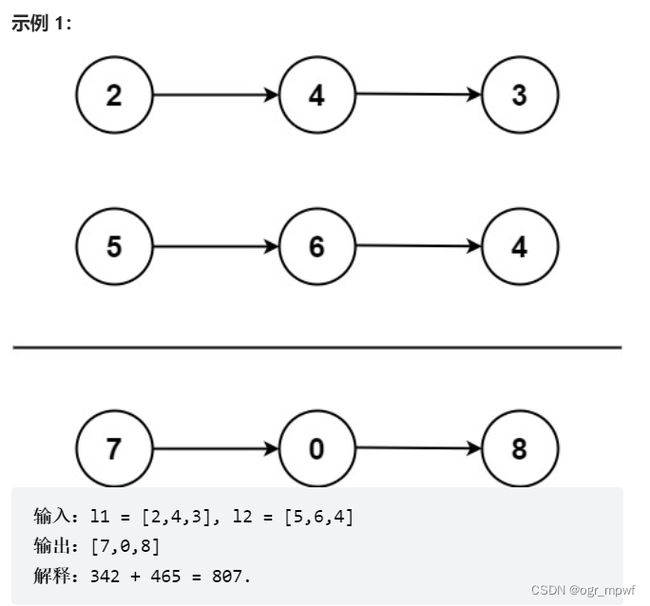
给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储一位数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
1.2 核心思路
采用模拟思想。首先,创建result存储最终结果,add存储对应两个数相加后的进位项。对于链表L1和链表L2来说,依次遍历两个链表。
- 若L1.val+L2.val+add>=10,则存在进位项,更新add,并对L1.val+L2.val+add取余然后加入result中。
- 若L1.val+L2.val+add<10,则不存在进位项,add=0
当L1和L2其中一个链表遍历完后,可能会存在L1和L2其中一个还未到达链表末尾。此时,如果add为0,那么直接将声誉链表接入result末尾;若add不为0,则将其加入剩余链表的第一个节点中,不断更新剩余链表节点的值,直至无进位。
【PS:若进位持续至最后一个节点,那么在result末尾新增一个节点,节点的值为add】
1.3 代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
result,add=ListNode(),0
ans=result
while l1 and l2:
num=l1.val+l2.val+add
result.next,add=ListNode(num%10,None),num//10
result,l1,l2=result.next,l1.next,l2.next
resL=l1 if l1 else l2
result.next=resL
while resL and add>0:
num=resL.val+add
resL.val,add=num%10,num//10
resL,result=resL.next,result.next
if not resL and add>0:
result.next=ListNode(add,None)
return ans.next
2.无重复字符的最长子串(滑动窗口+哈希表)
2.1 题目描述
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
2.2 核心思路
首先,设置start,end作为滑动窗口的起始和终止下标。满足start<=end,处于[start,end]中的字符串为无重复字符的字符串。同时利用hashset哈希表存储[start,end]中每个字符出现的次数。
- 若[start,end]中,s[end]出现的次数>1,那么将start向前移动,直到s[end]出现次数为1。【此时,可以保证处于[start,end]中的字符串为无重复字符的字符串】
- 若[start,end]中无重复字符,此时更新最大无重复字符串的长度,然后将end向前移动。并循环进行上述操作。
时间复杂度:O(n)
2.3 代码
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if len(s)==0:return 0
start,end,maxNum=0,0,1
hashset={s[start]:1}
while start<=end and end<len(s)-1:
end+=1
if s[end] in hashset:hashset[s[end]]+=1
else:hashset[s[end]]=1
while hashset[s[end]]>1 and start<=end:
hashset[s[start]]-=1
start+=1
maxNum=max(maxNum,end-start+1)
return maxNum
3.最长回文子串(动态规划)*
3.1 题目描述
给你一个字符串 s,找到 s 中最长的回文子串。
示例:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
3.2 核心思路
采用动态规划的思想dp[i][j]存储字符串s[i]到s[j]之间的子串是否为回文串。若s[i…j]为回文串,dp[i][j]=True,反之为False。
对于回文串的判定,根据回文串的特性,子串正序遍历和逆序遍历结果相同。因此,子串首尾元素必然是相同的。若在某一个回文串首尾分别加上相同的字符,那么得到新的子串仍然是回文串。
【例如:对于回文串aba来说,在其首尾分别加上c得到cabac,仍然是回文串】
因此,如果我们已知某一个字符串为回文串,那么只要首尾增加的元素相同,那么仍然可以得到一个回文串。存在以下两种情况:
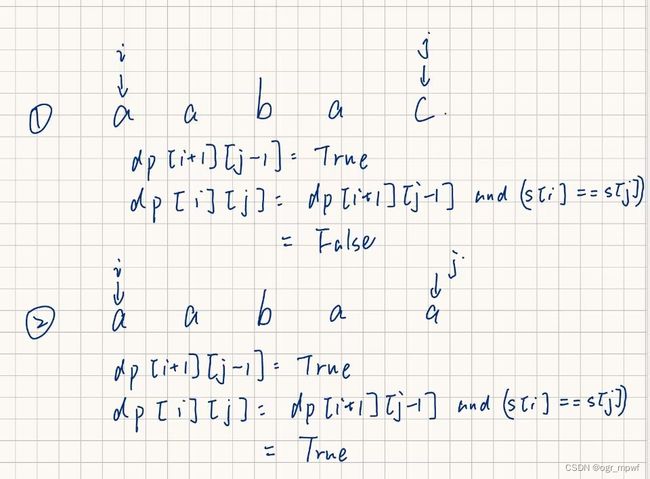
由此,可以得到递推公式:dp[i][j]=dp[i+1][j-1] and (s[i]==s[j]),其中i
- 步骤一:初始化dp,dp[i][i]=True。若子串仅存在一个字符,那么他必然是回文串。
- 步骤二:按照递推公式dp[i][j]=dp[i+1][j-1]依次计算dp列表。需要注意计算的顺序按照(0,1),(1,2),(2,3),…(0,2),(1,3),…这样的顺序进行【斜对角线】,因为dp[i][j]需要由dp[i+1][j-1]得到。
- 步骤三:在计算dp[i][j]时,更新回文串的最大长度,并记录i,j
3.3 代码
class Solution:
def longestPalindrome(self, s: str) -> str:
#isPalindrome[i][j]=True or False表示s[i,j]是否为回文子串
#isPalindrome[i][j]=isPalindrome[i+1][j-1] and s[i]==s[j]
n=len(s)
#初始化
isPalindrome=[[True]*n for i in range(n)]
#更新isPalindrome
maxLength,index_x,index_y=1,0,0
for k in range(1,n):
for i in range(0,n-k):
j=i+k
isPalindrome[i][j]=isPalindrome[i+1][j-1] and s[i]==s[j]
if isPalindrome[i][j] and j-i+1>maxLength:
index_x,index_y,maxLength=i,j,j-i+1
return s[index_x:index_y+1]
4.盛最多水的容器(双指针)*
4.1 题目描述
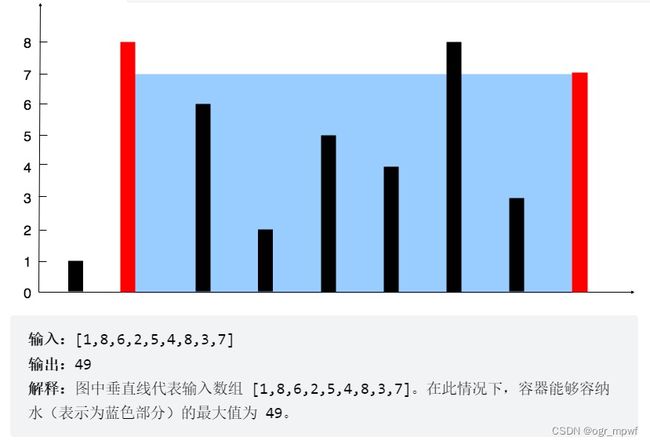
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
4.2 核心思路
采用双指针的方法实现。
【算法核心流程】
- 初始化指针:首先,start,end索引指向height的首尾。
- 计算盛水容积:然后,根据公式计算出此时盛水的容积:volumn=min(height[start],height[end])+(end-start)
- 更新指针:比较height[start],height[end],将height较小的下标向内部移动一位,循环计算盛水容积。同时更新最大容积时的下标。
【算法正确性验证】
为什么height较小的下标向内部移动一位?
根据盛水的容积:volumn=min(height[start],height[end])+(end-start)可以得到,当start+1或者end-1时,end-start的值必然会减少。此时min(height[start],height[end])存在两种情况:增大或者减小。若min(height[start],height[end])增大,则volumn的值可能会增大;若min(height[start],height[end])减小,则volumn的值必然减小。因此为了得到最大的volumn值,尽可能需要让min(height[start],height[end])的值增大。
- 若将height较小的下标向内部移动一位(假设height[start]
- 若将height较大的下标向内部移动一位(假设height[start]
- 若将height较大的下标向内部移动一位(假设height[start]
4.3 代码
class Solution:
def maxArea(self, height: List[int]) -> int:
start,end=0,len(height)-1
Maxvolumn=0
while start<end:
tempvolumn=min(height[start],height[end])*(end-start)
Maxvolumn=max(Maxvolumn,tempvolumn)
if height[start]<=height[end]:
start+=1
else:
end-=1
return Maxvolumn
5.电话号码的字母组合(递归,回溯)
5.1 题目描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
5.2 核心思路【还可以采用队列,后续补充】
采用回溯的思想,构造如下的递归树。可以看出,对于digits中每一个元素可能对应的字母,通过乘法原理进行排列组合,最终可以得到结果。
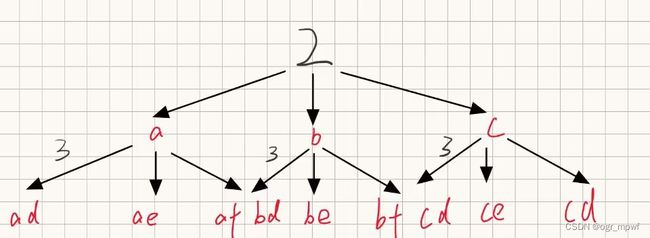
为了存储数字对应的字母,通过字典数据结构实现:
digitMap={
'2':['a','b','c'],
'3':['d','e','f'],
'4':['g','h','i'],
'5':['j','k','l'],
'6':['m','n','o'],
'7':['p','q','r','s'],
'8':['t','u','v'],
'9':['w','x','y','z']
}
然后,构造回溯函数backtracking,其要素如下:
- 参数:digits,result,index,tempresult,digitMap。其中digits表示当前还未组合字母的数字串,result存储最终结果,index表示digits[0]中即将选择的字母下标,tempresult存储一种可能字母组合结果。
- 终止条件:当digits为空时,得到了一种字母组合结果,因此将temresult加入result中,return。=
- 递归拆解:当digits不为空时,我们已知需要将digitMap[digits[0]]的第index个元素加入tempresult中,然后递归组合digits[1:]的后续数组字符串中的字母。此时对满足index
5.3 代码
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if digits=="":return []
digitMap={
'2':['a','b','c'],
'3':['d','e','f'],
'4':['g','h','i'],
'5':['j','k','l'],
'6':['m','n','o'],
'7':['p','q','r','s'],
'8':['t','u','v'],
'9':['w','x','y','z']
}
result=[]
def backtracking(digits,result,index,tempresult,digitMap):
if len(digits)==0:
result.append(tempresult)
return
while index<len(digitMap[digits[0]]):
backtracking(digits[1:],result,0,tempresult+digitMap[digits[0]][index],digitMap)
index+=1
backtracking(digits,result,0,"",digitMap)
return result
6.删除链表的倒数第N个结点(链表)
6.1 题目描述
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。

6.2 核心思路
【方法一:计算链表长度+从头正序遍历】
由于链表长度未知,因此,可以采用遍历一遍链表计算出链表长度,然后将倒数第n个数转化为正数第length-n+1个数;再次进行链表的遍历,找到需要删除的节点。
时间复杂度:O(n)
【方法二:栈】
栈数据结构可以逆序弹出栈顶元素,因此可以先将链表全部压入栈中,然后不断弹出,直到找到题目要求的节点,然后删除即可。
6.3 代码
【方法一】
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
#先找到链表长度,然后在从头遍历一遍
dummy=ListNode(-1,head)
listLength,index=-1,dummy
while index:
index=index.next
listLength+=1
n,preNode,Node=listLength-n,dummy,head
while n>0 and Node:
preNode=Node
Node=Node.next
n-=1
#删除节点
preNode.next=Node.next
return dummy.next
7.括号生成(回溯,递归)
7.1 题目描述
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
7.2 核心思路
采用回溯的思想,绘制递归树如下:
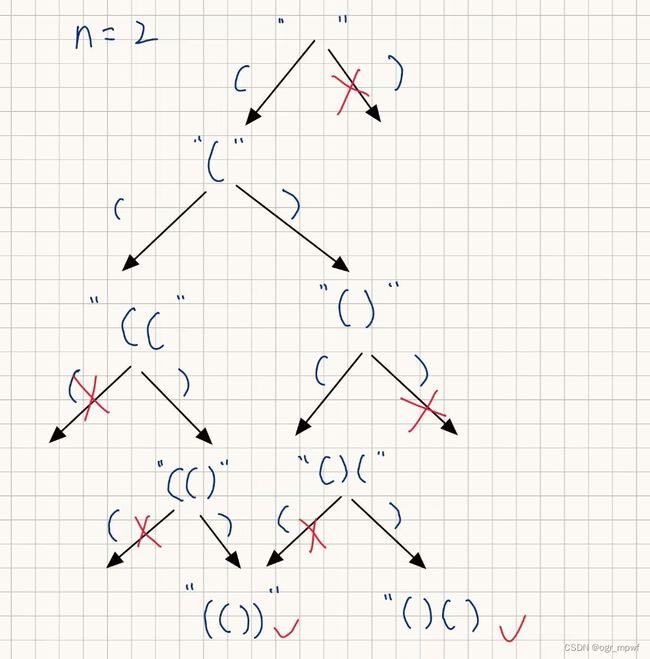
由上图可以看出,当n=2时,存在两种生成括号的方法。若以nLeft,nRight记录当前已经生成的左括号和右括号的数目,对于每一层的括号选择来说,可以得到如下的规则:
- 若nLeft
- 若nRight
- 若nLeft=nRight=n,则将结果加入result中,然后回溯。
- 若nRight
7.3 代码
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
result=[]
def backtracking(nLeft,nRight,n,tempParenthesis,result):
#tempParenthesis记录每一次生成的括号
if nLeft>n or nRight>n:
return
if nLeft==n and nRight==n:
result.append(tempParenthesis)
return
backtracking(nLeft+1,nRight,n,tempParenthesis+"(",result)
if nRight<nLeft:
backtracking(nLeft,nRight+1,n,tempParenthesis+")",result)
backtracking(0,0,n,"",result)
return result
8.组合总和(回溯,递归)
8.1 题目描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
8.2 核心思路
采用递归回溯的方法,通过backtracking函数实现回溯。回溯的要素如下:
- 参数:candidates,result,tempresult,target。candidates为可以候选的数组,result存储所有组合结果,tempresult存储一次结果。target为当前目标数【target+tempresult中的数为题目要求的组合结果之和】
- 递归终止条件:当target=0时,无需继续向tempresult中加入数字,因此将tempresult加入result中,然后返回;当candidates中没有可以继续选择的候选数时,回溯上一层,返回。
- 递归拆解:当target>=candidates[0]时,说明candidates中第一个元素可以加入tempresult中,此时递归调用函数:backtracking(candidates,result,tempresult+[candidates[0]],target-candidates[0]);当target
8.3 代码
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result=[]
def backtracking(candidates,result,tempresult,target):
if target==0:
result.append(tempresult)
return
if len(candidates)==0:
return
if target>=candidates[0]:
backtracking(candidates,result,tempresult+[candidates[0]],target-candidates[0])
backtracking(candidates[1:],result,tempresult,target)
backtracking(candidates,result,[],target)
return result
9.全排列(回溯)
9.1 题目描述
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
9.2 核心思路
采用递归回溯的方法,实现数组的全排列,对于[1,2,3]构造如下的递归树:

采用递归回溯的方法,通过backtracking函数实现回溯。回溯的要素如下:
- 参数:nums,result,tempresult。nums为需要全排列的数组,result存储所有全排列结果,tempresult存储一次结果。
- 递归终止条件:当tempresult为一组全排列时,无需继续向tempresult中加入数字,因此将tempresult加入result中,然后返回。
- 递归拆解:当tempresult不为一组全排列时,向tempresult中加入剩余不存在于tempresul中的数,遍历nums,选择nums[i] not in tempresult,backtracking(nums,result,tempresult+[nums[i]])
9.3 代码
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
result=[]
def backtracking(nums,result,tempresult):
if len(tempresult)==len(nums):
result.append(tempresult)
return
for i in range(len(nums)):
if nums[i] not in set(tempresult):
backtracking(nums,result,tempresult+[nums[i]])
backtracking(nums,result,[])
return result
10.子集(回溯)
10.1 题目描述
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
10.2 核心思路
采用回溯递归的思想,实现计算数组的子集,对于[1,2,3]构造如下的递归树:
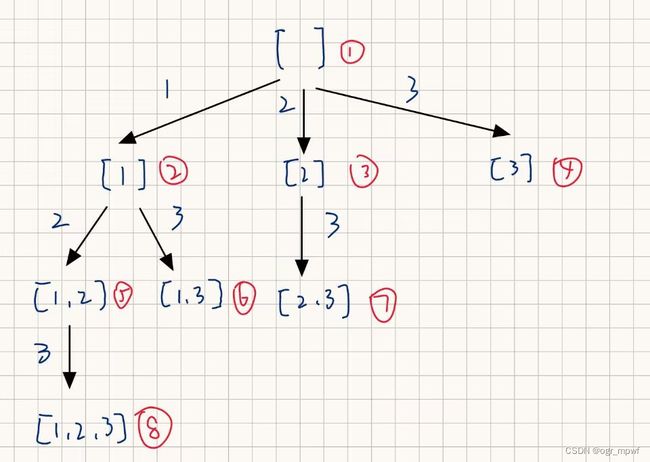
采用递归回溯的方法,通过backtracking函数实现回溯。回溯的要素如下:
- 参数:nums,result,tempresult,n。nums为可加入子集的候选数字,result存储所有子集结果,tempresult存储每一个子集,n表示子集最大长度。
- 递归终止条件:当tempresult为超过子集的最大长度时,无需继续向tempresult中加入数字返回;若nums为空,则返回。
- 递归拆解:每执行一次函数,首先将tempresult加入result中;然后遍历nums,将nums[i]加入子集tempresult中,并将nums[i+1:]作为候选数组,递归backtracking(nums[i+1:],result,tempresult+[nums[i]],n)
10.3 代码
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result=[]
def backtracking(nums,result,tempresult,n):
if len(tempresult)>n:return
result.append(tempresult)
if len(nums)==0:return
for i in range(len(nums)):
backtracking(nums[i+1:],result,tempresult+[nums[i]],n)
backtracking(nums,result,[],len(nums))
return result