机器学习入门（二）：KNN分类算法和决策边界(Decision Boundary)绘制
机器学习入门专栏其他章节：
机器学习入门（一）线性回归
机器学习入门（三）朴素贝叶斯
机器学习入门（四）决策树
机器学习入门（五）集成学习
机器学习入门（六）支持向量机
机器学习入门（七）多项式回归
机器学习入门（八）主成分分析
机器学习入门（九）无监督学习
1）KNN算法基础知识：
KNN全称K Nearest Neighbor, k是指最近邻居的个数。
俗话说物以类聚，人以群分，我们通常判别一个人是好是坏的方式就是看他周围是一群好人还是坏人。
这个算法也是如此，假如A的周围有一堆好人，我们就认为他是个好人。即使他周围有两个坏人（干扰项），我们也不会把它当成坏人。
而人与人的关系也有远近之分，计算远近，我们就需要用距离来衡量，有时候远亲不如近邻就体现了距离的重要性。
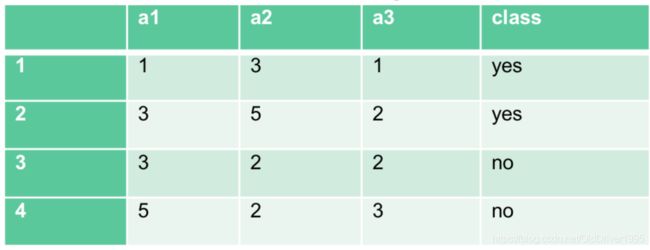
首先看这样一个例子：
现在有一个点，坐标分别是a1=2，a2=4，a3=3，请问它是yes还是no。
很简单，我们就用三维坐标距离公式计算：
可以很直观地发现，他离第二个点是最近的，如果k值取1，那他就直接划为yes，如果k取3，即用最近的三个邻居来衡量，发现点1，2，3都很近，2 yes 1 no，所以最后还是划成yes。
注意，虽然这里K取不同值结果不一样，但k确实会影响分类结果。
这种计算距离的方式就叫欧式距离(Euclidean Distance)，当然还有其他计算方式，比如曼哈顿距离（Manhattan Distance)，公式如下：
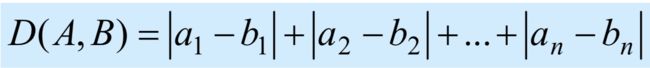
2）代码实现：
这里将用到sklearn包里面的iris数据，iris包含了三种花的各项物理参数，三种花分别叫setosa，versicolor，virginica。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
#导入iris数据
from sklearn.datasets import load_iris
iris = load_iris()
X=iris.data
y=iris.target
X=X[:,:2] #只取前两列
X_train, X_test, y_train, y_test = train_test_split(
X, y, stratify=y, random_state=42) #划分数据，random_state固定划分方式
#导入模型
from sklearn.neighbors import KNeighborsClassifier
#训练模型
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
#查看各项得分
print("y_pred",y_pred)
print("y_test",y_test)
print("score on train set", knn.score(X_train, y_train))
print("score on test set", knn.score(X_test, y_test))
print("accuracy score", accuracy_score(y_test, y_pred))
结果如下:
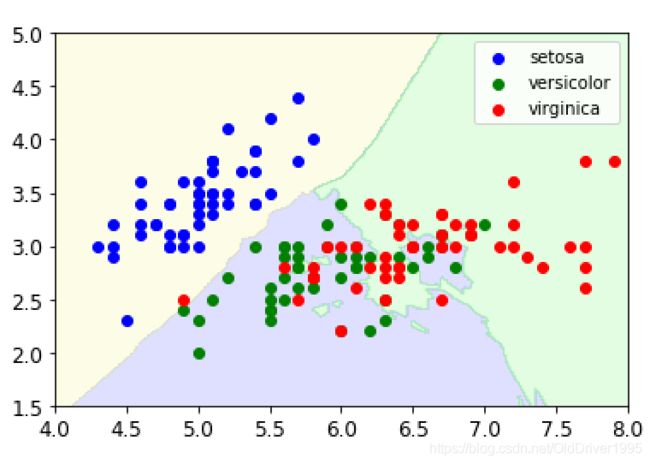
3)绘制决策边界：
这里将利用等高线图来画：
def plot_decision_boundary(clf , axes):
xp=np.linspace(axes[0], axes[1], 300) #均匀300个横坐标
yp=np.linspace(axes[2], axes[3], 300) #均匀300个纵坐标
x1, y1=np.meshgrid(xp, yp) #生成300x300个点
xy=np.c_[x1.ravel(), y1.ravel()] #按行拼接，规范成坐标点的格式
y_pred = clf.predict(xy).reshape(x1.shape) #训练之后平铺
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, y1, y_pred, alpha=0.3, cmap=custom_cmap)
plot_decision_boundary(knn, axes=[4, 8, 1.5, 5])
#画三种类型的点
p1=plt.scatter(X[y==0,0], X[y==0, 1], color='blue')
p2=plt.scatter(X[y==1,0], X[y==1, 1], color='green')
p3=plt.scatter(X[y==2,0], X[y==2, 1], color='red')
#设置注释
plt.legend([p1, p2, p3], iris['target_names'], loc='upper right')
plt.show()
绘制结果如图，方便深入理解knn算法：
可以发现有两种花由于混在一起，所以决策边界有点不不太容易划分。