【机器学习】线性回归(实战)
线性回归(实战)
目录
-
- 一、准备工作(设置 jupyter notebook 中的字体大小样式等)
- 二、构建实验所需的数据(以下实验将基于此数据)
- 三、实现线性回归的两种方式
-
- 方法一:通过直接求解得到拟合方程参数: θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy
- 方法二:通过梯度下降法进行求解(调用 sklearn 库中的方法)
- 四、常见的三种梯度下降策略
-
- 1、批量梯度下降(将所有数据的梯度均值作为下降的梯度)
- 2、随机梯度下降(随机选择一个点的梯度作为下降的梯度)
- 3、小批量梯度下降(选择一批数据点的梯度均值作为下降的梯度)
- 4、对 3 种策略进行对比
- 五、多项式回归
-
- 1、多项式回归的实现
- 2、最高次项对拟合效果的影响
- 六、实验:探究训练集规格对拟合的影响
- 七、实验:探究多项式回归的最高次项对拟合的影响
- 八、正则化
-
- 1、岭回归
- 2、Losso回归
实战部分将结合着 理论部分 进行,旨在帮助理解和强化实操(以下代码将基于 jupyter notebook 进行)。
一、准备工作(设置 jupyter notebook 中的字体大小样式等)
import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(51)
二、构建实验所需的数据(以下实验将基于此数据)
# 构造一个随机的散点图,以供拟合
# 用 rand() 函数随机生成一个 100*1 的矩阵,表示 x 坐标
X = 2*np.random.rand(100,1)
# 用已经生成的 x 坐标(矩阵),来构造一个函数 y = 3x+4
# 为了使得散点图足够“散”,再对该函数随机添加一定噪声
y = 4 + 3*X + np.random.randn(100,1)
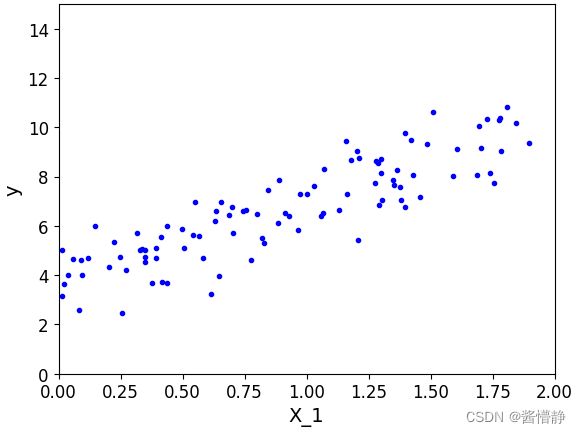
# 接下来绘制该图
# 设置图的 X 向量和 y 向量,第三个参数中,"b"表示绘制图的颜色是蓝色,"."表示该图不连线而仅绘制点图
plt.plot(X,y,'b.')
# 设置图的 x 轴名称
plt.xlabel('X_1')
# 设置图的 y 轴名称
plt.ylabel('y')
# [0,2,0,15] 限定坐标轴的大小(x的起始点终点,y的起始点终点)
plt.axis([0,2,0,15])
# 显示图片
plt.show()
绘制出构建的数据(散点图)
三、实现线性回归的两种方式
方法一:通过直接求解得到拟合方程参数: θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy
# 首先要给矩阵增加一列全为 1 的向量(该列实际上对应着偏置项)
X_b = np.c_[(np.ones((100,1))),X]
# 求出最终解:θ = (X^T^X)的逆矩阵 * X^T * y
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 这就是最终通过直接求解(没有“学习”)求出的 theta 矩阵(第一个值是拟合函数的偏置项、第二个是斜率)
theta_best
Out
array([[3.7195664 ],
[3.25523829]])
总结:把这个方法当作一个巧合就行。
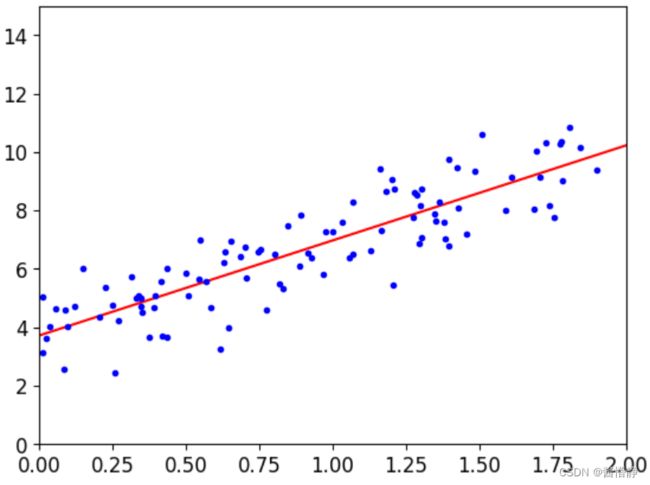
下面把通过“直接法”得到的拟合曲线绘制出来:
# 绘制拟合曲线
plt.plot(X_new,y_predict,'r-')
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
方法二:通过梯度下降法进行求解(调用 sklearn 库中的方法)
# 导入模块
from sklearn.linear_model import LinearRegression
# 实例化一个 线性回归 模型
lin_reg = LinearRegression()
# 用实例对数据进行训练(直接调用方法就可以了)
lin_reg.fit(X,y)
# 查看用模块算出的 theta 矩阵(两部分组成:偏置值、权重值)
# 打印偏置项
print(lin_reg.intercept_)
# 打印权重
print(lin_reg.coef_)
Out
[3.7195664]
[[3.25523829]]
可以看出,线性回归在采用直接法和梯度下降法时,得到的权重参数基本上是相同的。但是,直接求解法并不一定可解,且直接求解法没有体现出机器的“学习”过程,因此,在此只需要将这种方法作为一个巧合即可。
四、常见的三种梯度下降策略
1、批量梯度下降(将所有数据的梯度均值作为下降的梯度)
首先计算在所有数据上的损失值,然后再进行梯度下降。具体操作步骤是:遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,并更新梯度。这种方法每更新一次参数,都要把数据集里的所有样本计算一遍,因此得出的梯度往往都是朝着正确的方向;但是其缺陷是计算量过大,导致计算速度慢,因而不支持在线学习。
# 设置学习率(梯度下降的步长)
eta = 0.1
# 设置最大迭代次数
n_iterations = 1000
# 设置样本个数
m = 100
# 随机初始化权重参数
theta = np.random.randn(2,1)
for iteration in range(n_iterations):
# 计算梯度(每次将所有样本的梯度都算出来,然后再求平均)
gradients = 2/m*X_b.T.dot((X_b.dot(theta)-y))
# 梯度更新(即下降过程)
theta = theta - eta*gradients
# 查看最终的拟合参数
theta
Out
array([[3.7195664 ],
[3.25523829]])
可以看出,批量梯度下降算法计算得到的权重参数和前面算出的差距也是非常小的。
接下来插入一个 “学习率(步长)对梯度下降算法的收敛速度影响” 的实验。
# 定义一个记录在批量梯度下降下拟合参数变化的数组(之后用于绘图)
theta_path_bgd = []
# 由于等下要画图(学习率不同),因此这里封装一个函数
def plot_gradient_descent(theta,eta,theta_path = None):
# 计算样本个数,这里的 X_b 是全局的(定值)
m = len(X_b)
# 绘制原始数据(散点图)
plt.plot(X,y,"b.")
# 迭代
n_iterations = 1000
for iteration in range(n_iterations):
# 得到每次的预测结果
y_predict = X_new_exp.dot(theta)
# 画拟合直线
plt.plot(X_new,y_predict,'r-')
gradients = 2/m*X_b.T.dot((X_b.dot(theta)-y))
theta = theta - eta*gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("X_1")
plt.axis([0,2,0,15])
plt.title("eta={}".format(eta))
# 生成一个随机的初始拟合参数
theta = np.random.randn(2,1)
# 设置画布的规格
plt.figure(figsize = (10,4))
# 绘制一列,一列画3个,画第1个
plt.subplot(131)
plot_gradient_descent(theta,0.02)
# 绘制一列,一列画3个,画第2个
plt.subplot(132)
plot_gradient_descent(theta,0.1,theta_path_bgd)
# 绘制一列,一列画3个,画第3个
plt.subplot(133)
plot_gradient_descent(theta,0.5)
# 展示
plt.show()
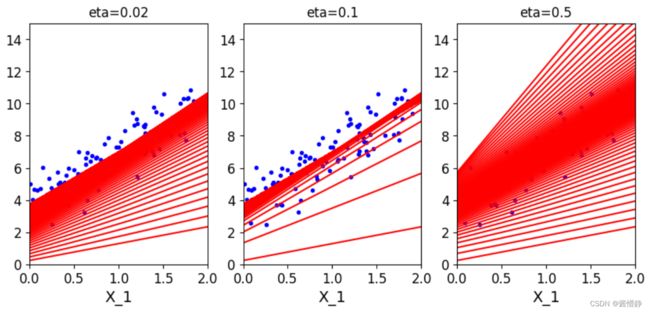
可见,步长越长,迭代越快,但有可能出现在一个值附近不断抖动的现象(有时甚至错过最优解);步长越小,迭代速度越慢,但不易错过最优解。所以算法的步长通常需要经过多次运行才能得到一个较优的值。
2、随机梯度下降(随机选择一个点的梯度作为下降的梯度)
不使用全部的样本来计算梯度,而是使用单一样本来近似估计梯度。具体的操作步骤是:每次从训练集中随机选择一个样本,计算其对应的损失和梯度,进行参数更新,反复迭代。这种方式在数据规模比较大时可以减少计算复杂度,提高计算效率。从概率意义上来说,单个样本的梯度是对整个数据集合梯度的无偏估计,但是它存在着一定的不确定性,因此收敛速率比批梯度下降得更慢(即,有可能会走很多弯路)。
# 定义一个记录在随机梯度下降下拟合参数变化的数组(之后用于绘图)
theta_path_sgd = []
# 获取样本数据点个数
m = len(X_b)
# epoch 是指整个数据样本要被轮训的次数
n_epochs = 50
theta = np.random.randn(2,1)
np.random.seed(43)
# 随意设置的 衰减策略 参数
t0 = 5
t1 = 50
# 衰减策略(迭代过程中,步长慢慢降低)
# 就像挖宝藏一样,最初不知道宝藏位置时,可以在全局进行较大范围的搜索(步长大一些)
# 随着迭代的进行,当慢慢锁定了最优解的大致范围时,就可以将步长降低,进行较为仔细的搜索
def learning_schedule(t):
return t0/(t1+t)
for epoch in range(n_epochs):
# 每个 epoch 中训练整个样本
for i in range(m):
# 只绘制前几步
if epoch<10 and i<10:
y_predict = X_new_exp.dot(theta)
plt.plot(X_new,y_predict,'r-')
# 随机选择一个索引
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
# 计算梯度
gradients = 2* xi.T.dot(xi.dot(theta)-yi)
# 更新学习率
eta = learning_schedule(n_epochs*m+i)
# 更新 theta
theta = theta - eta*gradients
# 添加至路径中
theta_path_sgd.append(theta)
# 绘散点图
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
3、小批量梯度下降(选择一批数据点的梯度均值作为下降的梯度)
将数据分为若干批次,按批次更新参数(每一批样本被称为 MiniBatch,规模通常取 2 )。每一批次中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性;另一方面,由于一批样本的数量比整个数据集少很多,因此计算量也不是很大。所以,相较其他梯度下降算法,小批量梯度下降是用得比较多的。
# 定义一个记录在小批量梯度下降下拟合参数变化的数组(之后用于绘图)
theta_path_mgd = []
# 每次选用的训练样本数量(小批量)
minibatch = 16
theta = np.random.randn(2,1)
np.random.seed(43)
t=0
for epoch in range(n_epochs):
# 在每次 epoch 中均置乱样本
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0,m,minibatch):
t += 1
xi = X_b_shuffled[i:i+minibatch]
yi = y_shuffled[i:i+minibatch]
gradients = 2/minibatch*xi.T.dot(xi.dot(theta)-yi)
eta = learning_schedule(t)
theta = theta - eta*gradients
theta_path_mgd.append(theta)
theta
Out
array([[3.64605615],
[3.32563198]])
可以看出,小批量梯度下降法计算得到的权重参数和前面的差距也是非常接近的。
4、对 3 种策略进行对比
# 将前面得到的 3 个列表转换为 npArray
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
# 绘制 3 种算法在计算拟合参数时,各自的变化情况
plt.figure(figsize=(12,8))
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r--',linewidth=1,label='SGD')
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=2,label='MINIGD')
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=3,label='BGD')
plt.legend(loc='upper left')
plt.xlabel("X")
plt.ylabel("y")
plt.axis([3.1,3.7,3.2,4])
plt.show()
五、多项式回归
1、多项式回归的实现
前面的拟合,都是针对线性函数进行的,当待拟合数据呈非线性形状时要如何执行回归呢?这就需要用到多项式回归了。Sklearn 中也是提供了现成的库函数以供调用,下面对多项式回归的使用进行一个实验:
# 重写构建一些随机点(准备100个)
m = 100
# 设置 x 坐标范围为 [-3,3]
X = 6*np.random.rand(m,1)-3
# 随机设置一个 f(x) , np.random.randn()是一个高斯分布
y = 0.5*X**2 + X + np.random.randn(m,1)
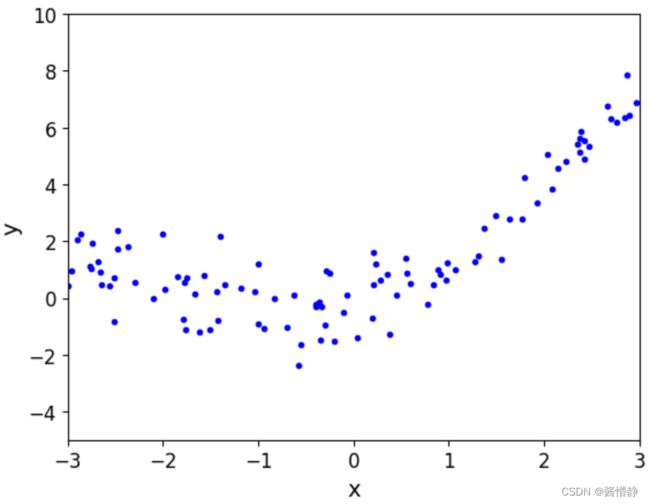
# 绘图
plt.plot(X,y,'b.')
plt.xlabel('x')
plt.ylabel('y')
plt.axis([-3,3,-5,10])
plt.show()
# 引入更强大功能的包(能够对高次项进行拟合)
from sklearn.preprocessing import PolynomialFeatures
# 该步骤中 degree 的值指示构成的多项式中的最高项,bias 为假表示式中无 xy 项目
poly_features = PolynomialFeatures(degree = 2,include_bias = False)
# fit_transform 操作会将 X 在 x^2^ 、 x 项的值分别求出(在向量中的顺序是从低次项到高次项),并反馈出结果
# fit 是计算各个项上的值
# transform 是将计算出的值进行格式化反馈
X_poly = poly_features.fit_transform(X)
# 任取一组数据进行查看
print(X_poly[0])
print(X_poly[0][0]**2)
print(len(X_poly))
Out
[-0.25217238 0.06359091]
0.06359091007874637
100
可以看出,该数组中,排列顺序是从低次项到高次项;
其次,对于本实验的数据而言,其满足 X_poly[i][0]2 = X_poly[i][1]。
接下来就能根据新得到的参数矩阵,按照线性回归的方式进行拟合。
# 实例化一个线性回归器
linS_reg = LinearRegression()
# 用已经得到的 X_poly 开始训练以求出 theta 向量
linS_reg.fit(X_poly,y)
print(linS_reg.coef_)
print(linS_reg.intercept_)
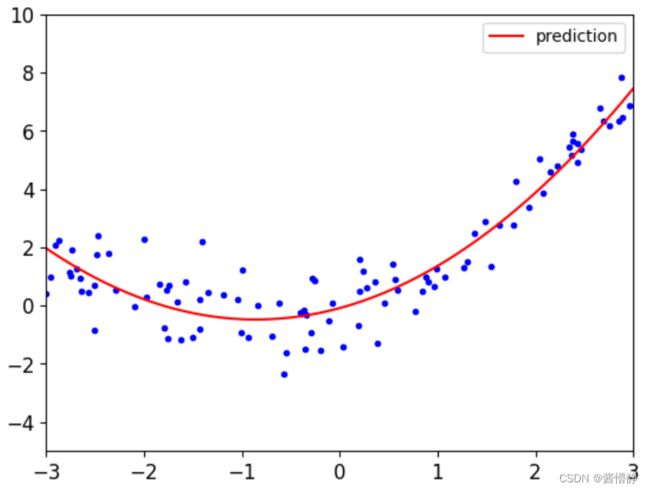
即 linS_reg 这个分类器最终得到的拟合函数为:y=0.53x2+0.91x-0.08,
前面我们定义的原函数为:y=0.5x2+x,可见拟合效果还是很不错的。
接下来绘制这条通过多项式回归得到的拟合曲线(图像才能直观地感受效果)。
# 绘图查看拟合效果
# 从 [-3,3] 等距选取 100 个点
X_new = np.linspace(-3,3,100).reshape(100,1)
# 用这 100 个点按前面已经构造好的方式求出对应的 x^2^ 与 x
# 注意:由于前面已经 fit 过了,因此再重复使用同等算法时只需要 transform 即可
X_new_poly = poly_features.transform(X_new)
# 用训练好的模型去对这个列向量进行求值
y_new = linS_reg.predict(X_new_poly)
# 绘图
plt.plot(X,y,'b.')
plt.plot(X_new,y_new,'r-',label='prediction')
plt.axis([-3,3,-5,10])
plt.legend()
plt.show()
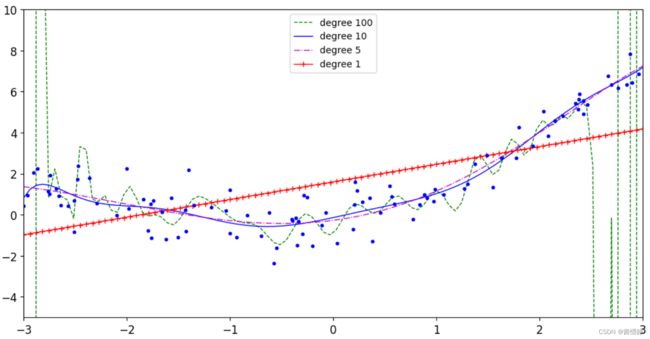
2、最高次项对拟合效果的影响
# 引入 Pipeline 包,该包可以将具有“流水线”性质的工作进行封装,以简化代码
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 设置图的大小
plt.figure(figsize=(12,6))
for style,width,degree in (('g--',1,100),('b-',1,10),('m-.',1,5),('r-+',1,1)):
# 1. 求出多项式的各项
poly_features = PolynomialFeatures(degree = degree,include_bias = False)
# 2. 标准化:当多项式中存在较高项时,其值会很大,因此需要进行标准化
std = StandardScaler()
# 3. 生成训练器
lin_reg = LinearRegression()
# 利用包对以上操作进行流水线封装
polynomial_reg = Pipeline([("poly_features",poly_features),
("StandardScaler",std),
("lin_reg",lin_reg)])
# 开始训练
polynomial_reg.fit(X,y)
# 预测
y_new_2 = polynomial_reg.predict(X_new)
plt.plot(X_new,y_new_2,style,label = "degree " + str(degree), linewidth = width)
# 绘图
plt.plot(X,y,'b.')
plt.axis([-3,3,-5,10])
plt.legend()
plt.show()
从上图可以看出,当函数模型过于复杂(如设置degree=100,远大于2)时,会出现龙格现象;
而当函数模型正常(如设置degree=2-10,比2大一些)时,取得的拟合效果往往还是挺不错的;
而当函数模型过于简单(如设置degree=1,此时其实就是线性回归了),取得的拟合效果就不太理想了。
六、实验:探究训练集规格对拟合的影响
数据少更容易产生过拟合现象还是数据多更容易?
# 导入计算均方误差的包来评估数据的拟合程度
from sklearn.metrics import mean_squared_error
# 导入对训练集进行划分的包
from sklearn.model_selection import train_test_split
# 此函数能得出某个学习器在样本数据变化(增加)时,其在训练集和验证集上的均方误差
def plot_learning_curve(model,X,y):
# 定义训练集、验证集、训练集标签、验证集标签
X_train, X_val, y_train, y_val = train_test_split(X,y,test_size = 0.2,random_state = 43)
# 训练集误差集合、验证集误差集合
train_errors,val_errors = [],[]
# 查看随着训练数据的增加,分类器在训练集和验证集上的均方误差变化
for m in range(1,len(X_train)):
# 将训练集中的前 m 个拿出来进行训练
model.fit(X_train[:m],y_train[:m])
# 将训练的学习器拿来对这 m 个样本进行预测
y_train_predict = model.predict(X_train[:m])
# 添加训练集中的均方误差
train_errors.append(mean_squared_error(y_train[:m],y_train_predict[:m]))
# 将训练的学习器拿来对验证集中的样本进行预测
y_val_predict = model.predict(X_val)
# 添加验证集中的均方误差
val_errors.append(mean_squared_error(y_val,y_val_predict))
# 绘图(由于 mse 取值较大,因此在这里将均方误差进行开方)
plt.figure(figsize=(8,5))
plt.plot(np.sqrt(train_errors),'r-',linewidth = 2,label = 'train_error')
plt.plot(np.sqrt(val_errors),'b-',linewidth = 2,label = 'val_error')
plt.xlabel('Trainging set size')
plt.ylabel('RMSE')
plt.legend()
# 绘制学习过程中的均方误差根曲线
lin_reg = LinearRegression()
plot_learning_curve(lin_reg,X,y)
plt.axis([0,80,0,4])
plt.show()
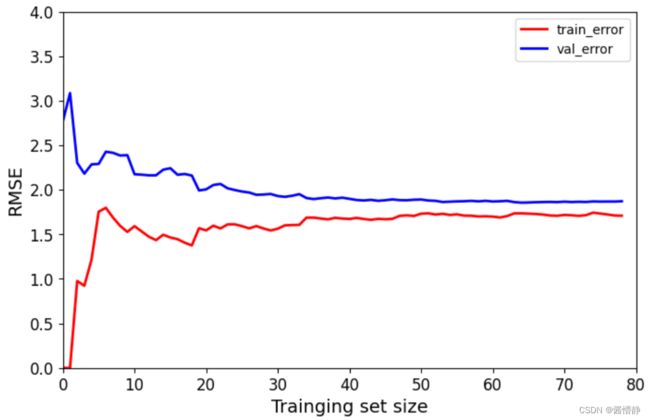
图像解读
蓝色线条是验证集上的均方误差根;红色线条是训练集上的均方误差根。
在一开始训练集很小时,分类器在训练集上的均方误差根很小,即拟合程度很好;而在验证集上的均方误差根很大,即拟合程度不好,这体现出此时的分类器出现了“过拟合”现象。而随着训练集的不断增加,随后在训练集上的均方误差根开始变大,但是这样的变大是必然的(因为训练样本增加,势必导致整体的均方误差会增大)。与之相反,在验证集上的均方误差开始变小,这体现出分类器的拟合能力开始逐渐优化。 另一方面,从整体来看,蓝色线条和红色线条慢慢靠近(即分类器在训练集和验证集上取得的实验效果开始趋于一致),这说明分类器的“过拟合”现象开始得到缓解,整个分类器的能力得到了优化。
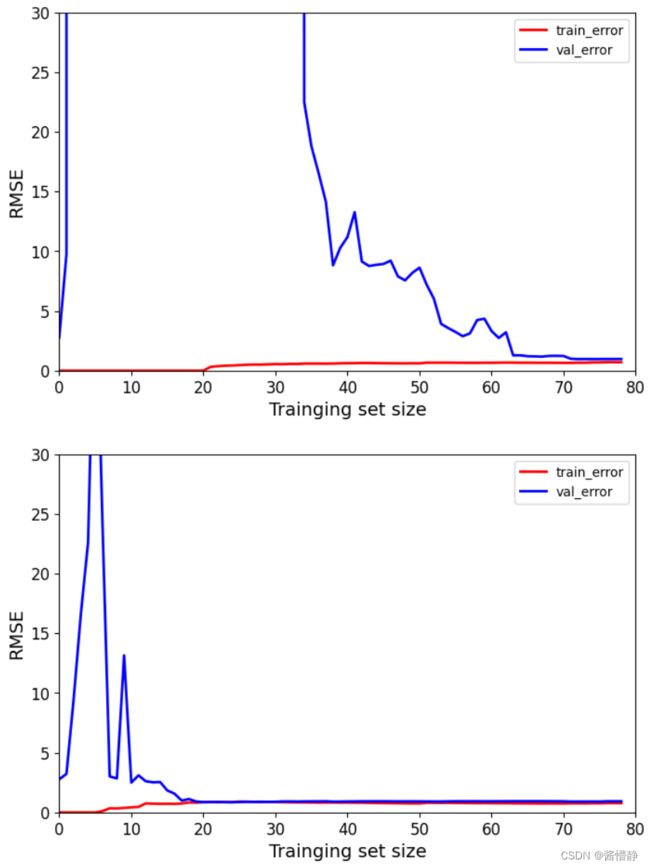
七、实验:探究多项式回归的最高次项对拟合的影响
# 建立一个最高次项达 20 的多项式回归模型
polynomial_reg = Pipeline([("poly_features",PolynomialFeatures(degree = 20, include_bias = False)),
("lin_reg",LinearRegression())])
# 绘制学习曲线
plot_learning_curve(polynomial_reg,X,y)
plt.axis([0,80,0,30])
plt.show()
# 建立一个最高次项达 5 的多项式回归模型
polynomial_reg = Pipeline([("poly_features",PolynomialFeatures(degree = 5, include_bias = False)),
("lin_reg",LinearRegression())])
# 绘制学习曲线
plot_learning_curve(polynomial_reg,X,y)
plt.axis([0,80,0,30])
plt.show()
从上图可以看出,当模型过于复杂时(比如函数中最高次项达到 20 ),其出现过拟合(即蓝线与红线的差值过大)的风险也越大(体现为:需要更多的样本进行训练,才能使得蓝线与红线贴近);而当模型较为简单时(比如函数中最高次项为 5 ),其出现过拟合的风险越低。
八、正则化
正则化是指在对不同的拟合方程进行评估时,额外再引入一项对拟合方程参数进行考察的新项目作为损失函数,以此来选出权重参数尽可能平滑的拟合系数。
1、岭回归
# 1. 岭回归(加平方项调整)
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
np.random.seed(42)
m = 80
X = 4*np.random.rand(m,1)
y = 0.5 * X + np.random.randn(m,1)/1.5 + 1
X_new = np.linspace(0,4,100).reshape(100,1)
def plot_model(model_class,alphas,**model_kargs):
for alpha,style in zip(alphas,('b--','g-','r:')):
model = model_class(alpha,**model_kargs)
model = Pipeline([("poly_features",PolynomialFeatures(degree = 15,include_bias = False)),
("StandardScaler",StandardScaler()),
("lin_reg",model)])
model.fit(X,y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new,y_new_regul,style,linewidth = lw, label = 'alpha={0} MSE={1:.4f}'.format(alpha,mean_squared_error(y, model.predict(X))))
plt.plot(X,y,'c.',linewidth = 3)
plt.legend()
plt.figure(figsize=(8,5))
plot_model(Ridge,alphas = (0,10**-5,1))
plt.show()
从上图可以看出,当 alpha 越大时,得到的决策方程越平稳,能有效避免过拟合现象。
2、Losso回归
# 2. lasso回归(加绝对值项调整)
from sklearn.linear_model import Lasso
plt.figure(figsize=(8,5))
plot_model(Lasso, alphas = (0,0.01,1))
plt.show()
这里得出的结果也是一致的:当 alpha 越大,得到的决策方程越平稳。