在运用之前我们需要知道他是什么?是怎么来的?怎么去应用。
傅立叶变换是一种分析信号的方法,它可分析信号的组成成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅立叶变换用正弦波作为信号的组成成分,在时域他们是相互重叠在一起的,我们需要运用傅里叶变换把他们分开并在频域显示出来。
连续傅里叶变换(Fourier Transform)如下:
连续傅里叶变换的反变换为:
满足傅里叶变换的条件是f(t)在整个定义域是绝对可积的(不发散),只有这样积分才有效。
快速傅里叶变换归属于离散傅里叶变换,理论部分大家可以自行百度。
那下面我们直接上代码:
1 import numpy as np 2 import time as tm 3 import math 4 #******************************************** 5 #这个函数的作用是输入转换点数,然后求出多少次方 6 #******************************************** 7 def __fft_inpute(x): 8 for i in range(11): 9 if(2**i == x): 10 return i 11 return -1 12 #************************ 13 #这个函数是把输入倒序排列 14 #************************ 15 def __fft_daoxu(x): 16 if(x == -1): 17 return -1 18 daoxu = [] 19 for i in range(2**x): 20 d = 0 21 for j in range(x): 22 if i & 1 == 1: 23 i >>= 1 24 d <<= 1 25 d += 1 26 else: 27 i >>= 1 28 d <<= 1 29 daoxu.append(d) 30 return daoxu 31 #**************************** 32 #快速傅里叶运算 基于时域的分解 33 #参数: 34 # data:是输入数据,以列表的形式传入 35 # N:输入链表data的长度 36 #**************************** 37 def fft(data,N): 38 _data =[] 39 _post_n = __fft_inpute(N)#判断运算级数 40 if(_post_n == -1): 41 return -1 42 43 44 daoxu_post = __fft_daoxu(_post_n) 45 print("原序列的倒置:",daoxu_post) 46 for i in daoxu_post: 47 _data.append(data[i]) 48 49 50 #蝶形运算,按时间抽选(DIT)的基-2 fft算法(库里-图基算法) 51 for i in range(_post_n):#第一次循环把就是各级运算分开 52 step = 1 << (i+1)#确定运算几大步, 53 54 Wn = 1.0 + 0.0j; #给定第一次旋转因子的值 55 56 print("第%d次蝶形运算"%(i)) 57 58 59 for j in range(int(step/2)):#不相同的Wn的个数 60 for x1 in range(j,N,step):#把同级的相同的Wn全部运算完 61 x2 = x1 + int(step / 2) 62 print(x1,x2) 63 64 #下面是两点傅里叶变换 65 tem_variable = 0 + 0j 66 tem_variable = (_data[x1].real + _data[x2].real*Wn.real - _data[x2].imag*Wn.imag) + (_data[x1].imag + _data[x2].real*Wn.imag + _data[x2].imag*Wn.real)*1j 67 _data[x2] = (_data[x1].real - _data[x2].real*Wn.real + _data[x2].imag*Wn.imag) + (_data[x1].imag - _data[x2].real*Wn.imag - _data[x2].imag*Wn.real)*1j 68 _data[x1] = tem_variable 69 70 71 Wn = (math.cos(2 * math.pi*(j +1) / (N >> (_post_n - (i + 1))))) - (math.sin(2 * math.pi*(j+1 )/ (N >> (_post_n - (i + 1)))))*1j#欧拉公式求旋转因子 72 73 74 return _data 75 76 num =[i for i in range(8)] 77 print("参与傅里叶变换的序列:",num) 78 star = tm.perf_counter() 79 print("我的fft:",fft(num,len(num)),len(num)) 80 end1 = tm.perf_counter() 81 print("numpy的fft:",np.fft.fft(num)) 82 end2 = tm.perf_counter() 83 print("自带库fft的运行时间:",end2 - end1,"我的fft的运行时间:",end1 - star)
下面我讲解下旋转因子:
Wn = (math.cos(2 * math.pi*(j +1) / (N >> (_post_n - (i + 1))))) - (math.sin(2 * math.pi*(j+1 )/ (N >> (_post_n - (i + 1)))))*1j#欧拉公式求旋转因子
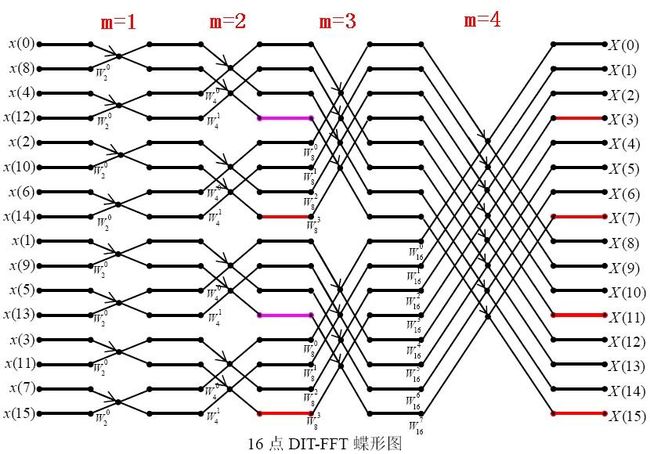
首先我们看一张图这个旋转因子是怎么变化的:
是不是恍然大悟,N的变化是从2开始,往右依次增加,增加的倍数是以前的两倍。所以我们可以写成如下形式变化:
1 (N >> (_post_n - (i + 1))
N的右移一次表现的效果就是除以一次2。
接下来看看我们的运行结果:
1 参与傅里叶变换的序列: [0, 1, 2, 3, 4, 5, 6, 7] 2 原序列的倒置: [0, 4, 2, 6, 1, 5, 3, 7] 3 第0次蝶形运算 4 0 1 5 2 3 6 4 5 7 6 7 8 第1次蝶形运算 9 0 2 10 4 6 11 1 3 12 5 7 13 第2次蝶形运算 14 0 4 15 1 5 16 2 6 17 3 7 18 我的fft: [(28+0j), (-3.9999999999999996+9.65685424949238j), (-4+4j), (-4+1.6568542494923797j), (-4+0j), (-4-1.6568542494923806j), (-3.9999999999999996-4j), (-3.9999999999999987-9.65685424949238j)] 8 19 numpy的fft: [28.+0.j -4.+9.65685425j -4.+4.j -4.+1.65685425j 20 -4.+0.j -4.-1.65685425j -4.-4.j -4.-9.65685425j] 21 自带库fft的运行时间: 0.00610923200000002 我的fft的运行时间: 0.003303109999999998
经过测试,长序列的傅里叶变换numpy自带的fft要快得多,这里只是验证程序的可行性。