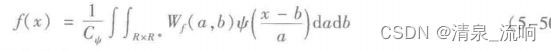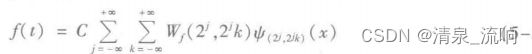传统语音增强——基于小波分解的语音降噪算法
一、小波分析的意义
在传统的傅里叶分析中,信号完全是在频域展开的,不包含任何时频的信息。因为丢弃的时域信息对某些应用同样重要,所以出现很多能表征时域和频域信息的信号分析方法,如短时傅里叶变换、Gabor变换、时频分析、小波变换等。其中,短时傅里叶变换是在傅里叶分析基础上引入时域信息的最初尝试,在假定一定长度时间窗内的信号是平稳的前提下,短时傅里叶变换可以通过将每个时间窗内的信号展开到频域的方法来获得局部的频域信息。但是,短时傅里叶变换的时域区分度只能依赖于大小不变的时间窗,对某些瞬态信号来说还是粒度太大。所以,对很多应用来说不够精确,短时傅里叶变换仍存在很大的缺陷。
而小波分析克服了短时傅里叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整。在一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率来提高频率的分辨率,在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。因为这些特性,小波分析可以探测正常信号中的瞬态,并展示其频率成分,被称为数学显微镜,广泛应用于各个时频分析领域。
二、小波分析的基本原理
小波是函数空间L^2(R)中满足下述条件的一个函数或者信号![]() (x):
(x):
式中,R*=R-{0}表示非零实数全体;![]() (w)是
(w)是![]() (x)的傅里叶变换;
(x)的傅里叶变换;![]() (x)称为小波母函数。
(x)称为小波母函数。
对于实数对(a,b),参数a为非零实数,函数
称为由小波母函数![]() (x)生成的依赖于参数对(a,b)的连续小波函数,简称小波。其中:a称
(x)生成的依赖于参数对(a,b)的连续小波函数,简称小波。其中:a称
为伸缩因子;b称为平移因子。
对信号f(x)的连续小波变换则定义为
其逆变换为
信号f(x)的离散小波变换定义为
其逆变换(恢复信号或重构信号)为
其中,C是一个与信号无关的常数。在MATLAB小波工具箱中提供了多种小波、包括Harr小波、Daubecheies(dbN)小波系、Symlets(symN)小波系、ReverseBior(rbio)小波系、Meyer (meyer)小波、Dmeyer(dmey)小波、Morlet(morl)小波、Complex Gaussian(cgau)小波系、Complex morlet(cmor)小波系、Lemarie(lem)小波系等。实际应用中应根据支撑长度、对称性、正则性等标准选择合适的小波函数。
三、小波降噪的基本原理
小波降噪是Donoho和Johnstone提出的,其主要理论依据是,小波变换具有很强的去数据相关性,它能够使信号的能量在小波域集中在一些大的小波系数中;而噪声的能量却分布于整个小波域内。因此,经小波分解后,信号的小波系数幅值要大于噪声的系数幅值。因此,幅值比较大的小波系数一般以信号为主,而幅值比较小的系数在很大程度上是噪声。于是,采用阈值的办法可以把信号系数保留,而使大部分噪声系数减小至零。小波降噪的具体处理过程为:将含噪信号在各尺度上进行小波分解,设定一个阈值,幅值低于该阈值的小波系数置为0,高于该阈值的小波系数或者完全保留,或者做相应的“收缩(shrinkage)”处理。最后,将处理后获得的小波系数用逆小波变换进行重构,得到去噪后的信号。阈值去噪中,阈值函数体现了对超过和低于阈值的小波系数不同处理策略,是阈值去噪中关键的一步。设w表示小波系数,T为给定阈值,sgn(*)为符号函数,常见的阈值函数主要有以下两种。
其他阈值函数
小波软阈值函数Wavelet_Soft
名称:Wavelet_Soft
功能:基于小波分解的软阈值法语音降噪。
调用格式:
signal = Wavelet_Soft(s,jN,wname)
说明:输入参数s是输入的含噪语音信号;jN为小波分解层数;wname是小波基名称。
signal是降噪后的信号。
函数程序如下:
function signal=Wavelet_Soft(s,jN,wname)
[c,l]=wavedec(s,jN,wname);
%高频分量的索引
first = cumsum(l)+1;
first1=first;
first = first(end-2:-1:1);
ld = l(end-1:-1:2);
last = first+ld-1;
%--------------------------------------------------------------------------
%软阈值
cxdsoft=c;
for j=1:jN %j是分解尺度
flk = first(j):last(j); %flk是di在c中的索引
thr(j)=sqrt(2*log((j+1)/j))*median(c(flk))/0.6745;
for k=0:(length(flk)-1) %k是位移尺度
djk=c(first(j)+k); %为了简化程序
absdjk=abs(djk);
thr1=thr(j);
if absdjk小波硬阈值函数Wavelet_Hard
名称: Wavelet_Hard
功能:基于小波分解的硬阈值法语音降噪。
调用格式:
signal = Wavelet_ Hard (s, jN, wname)
说明:输入参数s是输入的含噪语音信号;jN为小波分解层数;wname是小波基名称。
signal是降噪后的信号。
函数程序如下:
function signal=Wavelet_Hard(s,jN,wname)
[c,l]=wavedec(s,jN,wname);
%高频分量的索引
first = cumsum(l)+1;
first1=first;
first = first(end-2:-1:1);
ld = l(end-1:-1:2);
last = first+ld-1;
%--------------------------------------------------------------------------
%硬阈值
cxdhard=c;
for j=1:jN %j是分解尺度
flk = first(j):last(j); %flk是di在c中的索引
thr(j)=sqrt(2*log((j+1)/j))*median(c(flk))/0.6745;
for k=0:(length(flk)-1) %k是位移尺度
djk2=c(first(j)+k);
absdjk=abs(djk2);
thr1=thr(j);
%阈值处理
if absdjk信噪比计算函数SNR_Calc
名称:SNR_Calc
功能:计算信噪比。
调用格式:
snr=SNR_Calc(x,xn)
说明:输入信号x是输入的纯净语音信号;xn是输入的含噪信号。输出参数snr是计算的信噪比。
函数程序如下:
function snr=SNR_Calc(I,In)
% 计算带噪语音信号的信噪比
% I 是纯语音信号
% In 是带噪的语音信号
% 信噪比计算公式是
% snr=10*log10(Esignal/Enoise)
I=I(:)'; % 把数据转为一列
In=In(:)';
Ps=sum((I-mean(I)).^2); % 信号的能量
Pn=sum((I-In).^2); % 噪声的能量
snr=10*log10(Ps/Pn); % 信号的能量与噪声的能量之比,再求分贝值案例1、使用小波软阈值函数给带噪语音降噪
程序如下:
clear all; clc; close all;
[xx, fs] = audioread('C5_4_y.wav'); % 读入数据文件
xx=xx-mean(xx); % 消除直流分量
x=xx/max(abs(xx)); % 幅值归一化
N=length(x);
%-------------------------加入指定强度的噪声---------------------------------
SNR=5;
s=awgn(x,SNR,'measured','db'); % 叠加噪声
wname='db7';
jN=6; %分解的层数
snrs=20*log10(norm(x)/norm(s-x));
signal=Wavelet_Soft(s,jN,wname);
signal=signal/max(abs(signal));
snr1=SNR_Calc(x,s); % 计算初始信噪比
snr2=SNR_Calc(x,signal); % 计算降噪后的信噪比
snr=snr2-snr1;
fprintf('snr1=%5.4f snr2=%5.4f snr=%5.4f\n',snr1,snr2,snr);
% 作图
time=(0:N-1)/fs; % 设置时间
subplot 311; plot(time,x,'k'); grid; axis tight;
title('纯语音波形'); ylabel('幅值')
subplot 312; plot(time,s,'k'); grid; axis tight;
title(['带噪语音 信噪比=' num2str(SNR) 'dB']); ylabel('幅值')
subplot 313; plot(time,signal,'k');grid;%hold on;
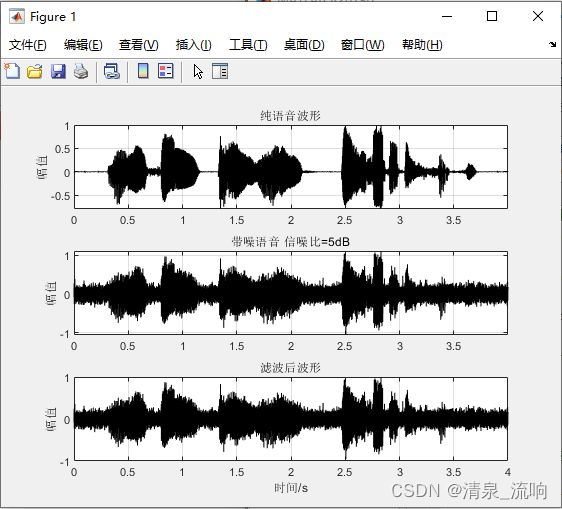
title('滤波后波形'); ylabel('幅值'); xlabel('时间/s');运行结果如下:
案例2、使用小波硬阈值函数给带噪语音降噪
程序如下:
clear all; clc; close all;
[xx, fs] = audioread('C5_4_y.wav'); % 读入数据文件
xx=xx-mean(xx); % 消除直流分量
x=xx/max(abs(xx)); % 幅值归一化
N=length(x);
%-------------------------加入指定强度的噪声---------------------------------
SNR=5;
s=awgn(x,SNR,'measured','db'); % 叠加噪声
wname='db7';
jN=6; %分解的层数
snrs=20*log10(norm(x)/norm(s-x));
signal=Wavelet_Hard(s,jN,wname);
signal=signal/max(abs(signal));
snr1=SNR_Calc(x,s); % 计算初始信噪比
snr2=SNR_Calc(x,signal); % 计算降噪后的信噪比
snr=snr2-snr1;
fprintf('snr1=%5.4f snr2=%5.4f snr=%5.4f\n',snr1,snr2,snr);
% 作图
time=(0:N-1)/fs; % 设置时间
subplot 311; plot(time,x,'k'); grid; axis tight;
title('纯语音波形'); ylabel('幅值')
subplot 312; plot(time,s,'k'); grid; axis tight;
title(['带噪语音 信噪比=' num2str(SNR) 'dB']); ylabel('幅值')
subplot 313; plot(time,signal,'k');grid;%hold on;
title('滤波后波形'); ylabel('幅值'); xlabel('时间/s');运行结果如下:
实验使用到的语音数据下载链接如下:
传统语音增强——最小方均(LMS)自适应滤波算法-数据集文档类资源-CSDN下载
参考文献:语音信号处理实验教程;梁瑞宇、赵力、魏昕(编著)