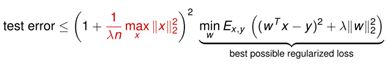issue2：overfitting and regularization

数据训练时分为训练集和测试集，在训练集上训练模型得到的误差叫做test err，在测试集上测试得到的误差就做test err。

我们最终的目标是在训练集上的test err足够小，这样表示模型能很好的fit这个类型的数据。

对于上节中的最小二乘问题，有如下等式：

 

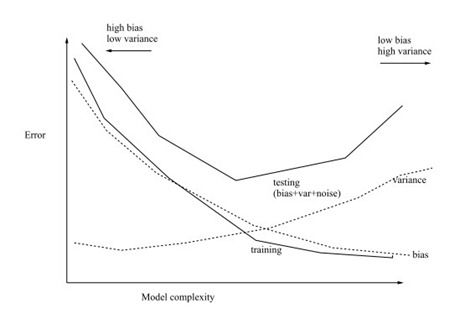
模型复杂度（complexity）即是描述训练误差和测试误差的不同的工具。

泛化（由训练集到测试集）误差：在很大的概率上，有 【待证明】（VC dimension）

模型复杂度即使式子中的O(d/n)，其中d是特征的数目，即#feature，n是训练数据的个数。即test err最大不会超过training err加上模型复杂度。

下图为bias-variance trade-off：

可知，当d << n的时候，训练误差会保持在一个很好的范围内，不会太大。但是当d非常大的时候，就需要，另一种表示形式。

通过在Loss function上面加上正则项（regularization），将模型参数的解空间限制在一定的范围内，可以保证模型复杂度不是随着d的增大而增长。

关于正则项具体内容，会单独一节讲，目前不care这个内容。

限制其解空间使得 成立。其中A是解空间限制的范围。g(w)可以使不同的表达解空间大小的范式，最常用的是L1-norm和L2-norm。

通过限制解空间，可以使模型复杂度成为A的函数，而不是d的函数。只要限制了A，不论d的变化，都可以保证泛化误差在一定的范围内（acceptable）。

同样可以保证解的稳定性（stable），因为限制了解空间，所有的参数对模型得到的结果都不会产生巨大的影响，因为权重本身很少。这样对一些outliers都有很强的鲁棒性。

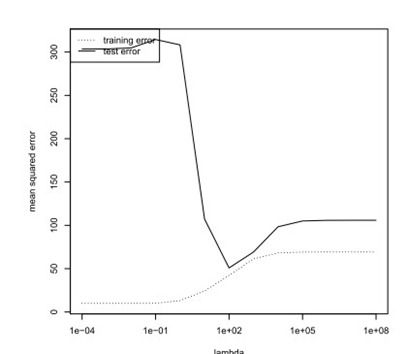
加图了regularization之后的模型复杂度如下：

也可以从Loss function优化的结果上来看，在L2-norm的regularization下，最小二乘法得到的结果是

在X转置乘以X之后加入了I矩阵。这种情况下，会有很强的抗干扰性，因为这种情况下保证矩阵是满秩的。求逆的结果总是存在。如果不加入正则项，上述逆矩阵不一定会存在，尤其是X中有两维数据非常相似的情况下，矩阵相乘的结果很可能不满秩或者近似不满秩，造成解空间会有很大的扰动。

关于模型复杂度的generalization bound：

假设对最小二乘法获得的Loss function使用L2-norm：

则泛化误差的界如下： 【待证明】

可见泛化误差不在于#feature相关，而死于lamda相关。

所以，如果在实际训练中获得了比较大的权重，则要加倍小心，因为很可能会产生overfitting的情况。