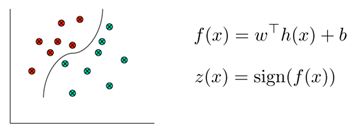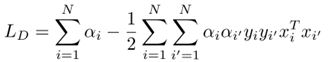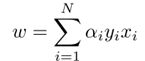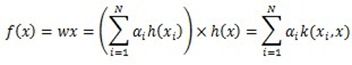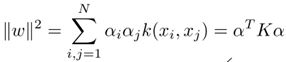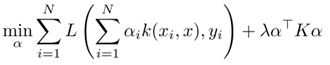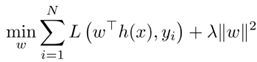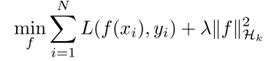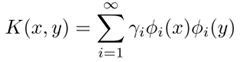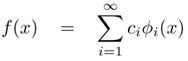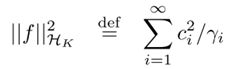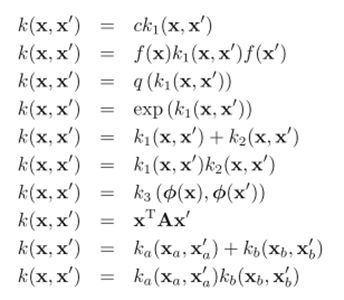issue6：DEEPLY SVM: from basis expansion to kernel
basis是一个具有魔力的东西，在数学中就是如此，他可以把一个函数通过基底变换搞成各种不同的样子，例如平面上的一个圆![Z0]KCF3$`2X8F)47_8%R}5H](http://images.cnblogs.com/cnblogs_com/ASenVJ/201208/20120813095142616.jpg "Z0]KCF3$`2X8F)47_8%R}5H"){kind=small}
，通过X=![}ZET7WHP}9VQ51}AU2]UH$4](http://images.cnblogs.com/cnblogs_com/ASenVJ/201208/20120813095142899.jpg "}ZET7WHP}9VQ51}AU2]UH$4"){kind=small}
，Y=
的基坐标转换，可以变成线性函数。
通常情况下的线性分类器如下：
![3){T`BPE])JHF@UL@)H}2NT](http://images.cnblogs.com/cnblogs_com/ASenVJ/201208/201208130951434421.jpg "3){T`BPE])JHF@UL@)H}2NT")
其中公式中的w和b是模型参数，x是特征，这里虽然是线性模型，但是可以通过将x映射为不用的基函数，可以把线性模型的函数直线打造成曲线的样式。在Andrew Ng的课件中，x称为attribute，而x的映射h(x)称为feature。
其中
。
基底变换提供了一种把线性不可分变成线性可分的方法，如下：
通过研究SVM的优化公式，可以找出一些有趣的fact，通过一系列的数学变换之后，可以得到对偶式：
它的解有如下形式：
直观来说，参数w的解存在于由x张成的实数空间中，因为y是分类值，只取两个不同的值对于二分类问题。可以简单证明，假设w的解超出了x组成的空间，那么w可以表示为
，其中
是x张成空间中的部分，而
是不在x张成空间中的部分，显然，这两部分是正交的。将这个解代入原公式中，可以把正交的部分全部消解掉。
总结上述问题，有如下结论：
Def. 如下一种Mercer核（Mercer核相关知识可以参阅《数据挖掘中的新方法——支持向量机》一书第三章，有详细的证明和解释）
可以把上述优化公式写成核的表示形式：
由以上三个公式，可以把原来w为参数的最优化公式转换为核函数表示的方式。
有上述公式可以看出，只要有了核，我们就不在需要基坐标转换公式h(x)了，因为都可以表示为核的形式。必然可以想象，核是对基坐标转换的一种替代。
核函数有如下的一些形式：
其中，上部分是生成核函数的基坐标转换函数，从左到右依次是多项式函数、高斯函数和logistic sigmoid函数。下部分是对应的核函数。简单看来，核提供了一种smooth的方法，越是接近中心的值越大，向两侧慢慢减弱，体现了一种平滑的能力。
通常来说，最优化的公式可以通过reformulation转化为不同形式，会有不同认识。
普通的参数形式为
转换为对偶形式有
进一步可以转换为无参（non-parametric）形式
由上面的公式，可以很轻松由对偶形式导出无参形式，不在证明。
其中正则项转变成在核组成的希尔伯特空间中的函数f。这里的正则项表明了选择哪一个f(x)的偏好。即这个优化方式倾向于选择什么样子的预测函数。
由于核的对称半正定特性，可以对其求解特征值与特征向量，假设可以表现为下面的形式：（注意特征分解结果并不和h(x)相同）
那么每个f(x)可以表示成
即把函数拆解到新的坐标系中，新坐标系的坐标是特征向量。
kernel可以看做一种平滑算子，所有的特征向量中越平滑的向量具有越大的特征值，表示他的重要性越高。 （为何越大的特征值具有越好的平滑性）
可见，f(x)中特征值越小的维度，得到的惩罚就越大，可见，正则项倾向于让f(x)最平滑。
可见，选择不同的核函数以及正则项，就是我们对f(x)的不同预期。
所以，可以构造自己的分类器，只要选取了不同的loss function，不同的h(x)，不同的维度（有限维或者无限维）以及不同的优化方法。
附：核函数的构造运算法则
