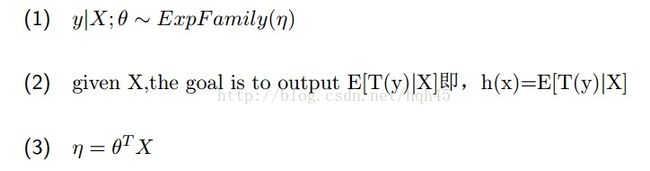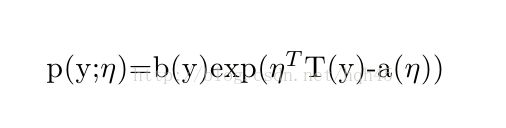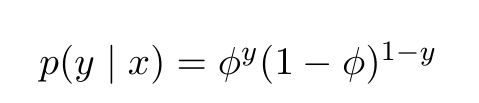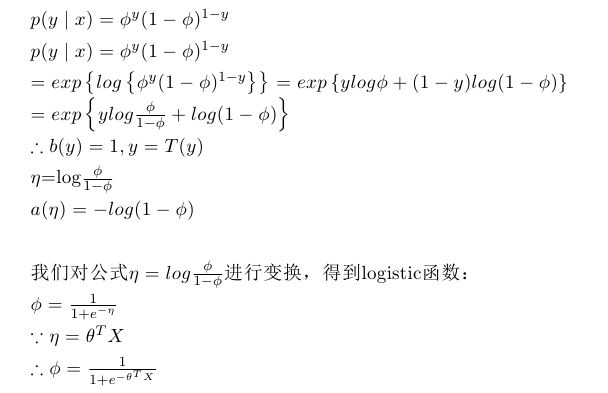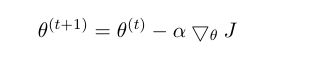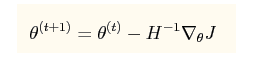广义线性模型与Logistic回归

一、广义线性模型

      广义线性模型应满足三个假设：

第一个假设为给定X和参数theta,Y的分布服从某一指数函数族的分布。

第二个假设为给定了X，目标是输出 X条件下T(y)的均值，这个T(y)一般等于y，也有不等的情况，

第三个假设是对假设一种的变量eta做出定义。

二、指数函数族

前面提到了指数函数族，这里给出定义，满足以下形式的函数构成了指数函数族：

其中a,b,T都是函数。

三、Logistic 函数的导出

Logistic回归假设P(y|x)满足伯努利Bernouli分布即

我们的目标是在给定X的情况下，能对参数phi进行建模，进而得到phi关于X的模型，怎么选择这个模型是一个问题，现在我们把满足努伯利分布的后验概率转化成指数函数族的形式，进而得出phi关于X的模型。

现在我们就得到了phi关于X的模型，参数是theta，同时我们要建立我们分类的假说模型：

这意味着如果我们得到了参数theta，对于给定的x就可以得到y=1的概率，则y=0的概率也可以求出，问题也就解决了，下面是讲怎么求解参数theta。

四、目标函数与梯度

现在我们已经知道了Logistic回归模型的形式，那么为了得到最优的参数，我们利用最大似然估计对theta进行估计。

现在我们已经得到了优化函数的导数， 利用最速下降法可以得到参数更新公式：

利用牛顿法求解最小值也是可以的，这里会用到Hessian矩阵

牛顿法的参数更新公式为

当然也可以用其他的最优化的算法，BGGS,L-BFGS等等。

五、Matlab实验

实验中的是mnist数据库，用到了其中的手写数字0和1的数据，用的是梯度下降法求解。

%%======================================================================
%% STEP 0: Initialise constants and parameters
%
%  Here we define and initialise some constants which allow your code
%  to be used more generally on any arbitrary input. 
%  We also initialise some parameters used for tuning the model.

inputSize = 28 * 28+1; % Size of input vector (MNIST images are 28x28)
numClasses = 2;     % Number of classes (MNIST images fall into 10 classes)

% lambda = 1e-4; % Weight decay parameter

%%======================================================================
%% STEP 1: Load data
%
%  In this section, we load the input and output data.
%  For softmax regression on MNIST pixels, 
%  the input data is the images, and 
%  the output data is the labels.
%

% Change the filenames if you've saved the files under different names
% On some platforms, the files might be saved as 
% train-images.idx3-ubyte / train-labels.idx1-ubyte

images = loadMNISTImages('mnist/train-images-idx3-ubyte');
labels = loadMNISTLabels('mnist/train-labels-idx1-ubyte');


index=(labels==0|labels==1);

images=images(:,index);
labels=labels(index);

inputData = [images;ones(1,size(images,2))];


% Randomly initialise theta


%%======================================================================
%% STEP 2: Implement softmaxCost
%
%  Implement softmaxCost in softmaxCost.m. 

% [cost, grad] = logisticCost(theta, inputSize,inputData, labels);
                                     


%%======================================================================
%% STEP 4: Learning parameters
%
%  Once you have verified that your gradients are correct, 
%  you can start training your softmax regression code using softmaxTrain
%  (which uses minFunc).

options.maxIter = 100;
options.alpha = 0.1;
options.method = 'Grad';
theta = logisticTrain( inputData, labels,options);
                          
% Although we only use 100 iterations here to train a classifier for the 
% MNIST data set, in practice, training for more iterations is usually
% beneficial.

%%======================================================================
%% STEP 5: Testing
%
%  You should now test your model against the test images.
%  To do this, you will first need to write softmaxPredict
%  (in softmaxPredict.m), which should return predictions
%  given a softmax model and the input data.

images = loadMNISTImages('mnist/t10k-images-idx3-ubyte');
labels = loadMNISTLabels('mnist/t10k-labels-idx1-ubyte');

index=(labels==0|labels==1);
images=images(:,index);
labels=labels(index);

inputData = [images;ones(1,size(images,2))];

% You will have to implement softmaxPredict in softmaxPredict.m
[pred] = logisticPredict(theta, inputData);

acc = mean(labels(:) == pred(:));
fprintf('Accuracy: %0.3f%%\n', acc * 100);

% Accuracy is the proportion of correctly classified images
% After 100 iterations, the results for our implementation were:
%
% Accuracy: 92.200%
%
% If your values are too low (accuracy less than 0.91), you should check 
% your code for errors, and make sure you are training on the 
% entire data set of 60000 28x28 training images 
% (unless you modified the loading code, this should be the case)

function [modelTheta] = logisticTrain(inputData, labels,option)

if ~exist('options', 'var')
    options = struct;
end

if ~isfield(options, 'maxIter')
    options.maxIter = 400;
end

if ~isfield(options, 'method')
    options.method = 'Newton';
end

if ~isfield(options, 'alpha')
    options.method = 0.01;
end
theta = 0.005 * randn(size(inputData,1),1);
iter=1;

maxIter=option.maxIter;
alpha=option.alpha;
method=option.method;
fprintf('iter\tStep Length\n');
lastSteps=0;
while iter<=maxIter
    
    h=sigmoid(theta'*inputData);
%     cost=sum(labels'.*log(h)+(1-labels').*log(1-h),2)/size(inputData,2);
    grad=inputData*(labels'-h)';
    
    if strcmp(method,'Grad')>0
        steps=alpha.*grad;
%     else
%         H = inputData* diag(h) * diag(1-h) * inputData';
%         steps=-alpha.*H\grad;
    end
    theta=theta+steps;
    stepLength=sum(steps.^2)/size(steps,1);
    fprintf('%d\t%f\n',iter,stepLength);
    if abs(stepLength)<1e-9
        break;
    end
    iter=iter+1;
end
modelTheta=theta;

    function z=sigmoid(x)
        z=1./(1+exp(-1.*x));
    end
end

function [pred] = logisticPredict(theta, data)

% softmaxModel - model trained using softmaxTrain
% data - the N x M input matrix, where each column data(:, i) corresponds to
%        a single test set
%
% Your code should produce the prediction matrix 
% pred, where pred(i) is argmax_c P(y(c) | x(i)).

%% ---------- YOUR CODE HERE --------------------------------------
%  Instructions: Compute pred using theta assuming that the labels start 
pred=theta'*data>0.5;
% ---------------------------------------------------------------------
end

to be continued.....