【机器学习 - 2】：数据集的处理

训练集和数据集分离

---

训练集和数据集分离的原理：当我们获取一个数据集时，我们需要将其一小部分拿出来作为测试集，剩余的作为训练集。例如对于一个训练集，将其20%作为测试集，80%作为训练集，这20%的测试集是已经有目标值了的，将训练集进行拟合，获得模型，再通过测试集进行测试，获得最终结果，将最终结果和已知的目标值进行比对，可预测其训练模型的精确度。

以下使用sklearn中的knn算法进行预测，以识别鸢尾花为例。

• 先获取数据集，观察下图中y的值，可将0，1，2分别看做鸢尾花的不同种类。

from sklearn.datasets import load_iris
# 获取数据集
iris = load_iris()
X = iris.data
y = iris.target

• 由上图可看出数据集的目标值是有一定顺序的，我们需要将其打乱后再分出训练集和测试集，打乱用到的函数为np.random.permutation()，下图中shuffle_indexs里是0-150的随机索引

import numpy as np
shuffle_indexs = np.random.permutation(len(X))

• 打乱数据后开始取训练集和测试集，训练集取80%，测试集取20%

test_ratio = 0.2 # 取20%做测试集
test_size = int(len(X) * test_ratio)

test_indexs = shuffle_indexs[:test_size] # 测试集索引
train_indexs = shuffle_indexs[test_size:] # 训练集索引

# 获得训练集
X_train = X[train_indexs]
y_train = y[train_indexs]
# 获得测试集
X_test = X[test_indexs]
y_test = y[test_indexs]

• 调用sklearn中的knn算法，将训练集进行拟合，获得模型，测试集通过训练的模型，获得最终的预测结果，观察下图可看到y_predict和y_test（标准答案），大部分是相同的。

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)	# 拟合，获得模型

y_predict = knn_clf.predict(X_test)	# 获取测试集的最终结果

• 根据y_predict和y_test，计算出模型的准确度，每次运行获得的准确度都不一样，但是准确率都在90%以上，说明模型的准确度较高。

np.sum(np.array(y_predict == y_test, dtype='int'))/len(y_test)

获取最优模型

---

参数的不同，会导致模型的不同，从而我们需要找到最合适的参数，从而训练出最优的模型。

我们可以自定义一个train_test_split函数，获取到训练集和测试集数据。根据以上的代码，编写的函数如下：

import numpy as np
def train_test_split(X, y, test_ratio=0.2, random_state=None):
    if random_state:
        np.random.seed(random_state) # 设置随机种子
    shuffle_indexs = np.random.permutation(len(X))
    test_ration = test_ration
    test_size = int(len(X) * test_ratio)
    
    test_indexs = shffle_indexs[:test_size]
    train_indexs = shuffle_indexs[test_size:]
    
    # 训练集
    X_train = X[train_indexs]
    y_train = y[train_indexs]
    
    # 测试集
    X_test = X[test_indexs]
    y_test = y[test_indexs]
    
    return X_train, X_test, y_train, y_test

我们也可以使用sklearn中封装好的train_test_split

from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

超参数

超参数：在执行程序之前需要确定的参数。

举个例子：在knn分类器中，即KNeighborsClassifier(n_neighbors=3)，n_neighbors值的不同，会导致模型的准确率不同，我们需要不断调整参数，找到某个数更加拟合我们的数据，这就是超参数。

权重问题：在【机器学习 - 1】：knn算法这一篇文章里，我们举了一个使用knn算法判断肿瘤为恶性肿瘤或良性肿瘤的例子，这个例子中我们主要以离待预测点周围最近的3个点进行判断。
而在如下图的情况中，待预测点（绿点）离红点（良性肿瘤）比较近，则它更可能为良性肿瘤，若以上篇文章中的思路来判断，因为它周围有2两个恶性肿瘤（蓝点），所以它很可能为恶性肿瘤。根据以上两种判断情况，我们需要把距离和个数这两种判断特征都考虑进来。

即绿色的点离红色的点最近，我们可以给这些距离加一个权重，这样及时周围有两个蓝点，但红点最近的距离权重大于这两个蓝点的距离权重，绿色的点可能就为良性肿瘤

在KNeighborsClassifier()中可设置权重参数：weights
当weights=uniform时，不考虑距离带来的权重问题
当weights=distance时，距离作为计算的权重

我们先看一下KNeighborsClassifier()的源码（如下图2），weights默认为uniform，p=2这个p是距离方法（如下图1），当=1时为曼哈顿距离，p=2时为欧拉距离，p增大，计算距离的方法不同。在KNeighborsClassifier()中默认为欧拉距离

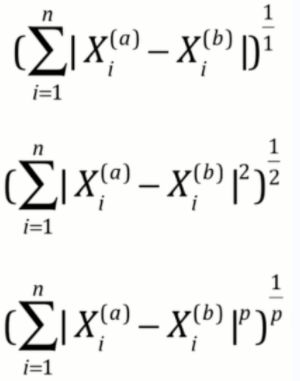
寻找最优模型

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)

%%time
best_k = 0
best_score = 0.0
best_clf = None
best_method = None
best_p = 0
for p in range(1, 6):
    for weight in ['uniform', 'distance']:
        for k in range(1, 21):
            knn_clf = KNeighborsClassifier(n_neighbors=k, weights=weight, p=p)
            knn_clf.fit(X_train, y_train)
            score = knn_clf.score(X_test, y_test)
            if score>best_score:
                best_score = score
                best_k = k
                best_clf = knn_clf
                best_method = weight
                best_p = p
print(best_k)
print(best_score)
print(best_clf)
print(best_method)
print(best_p)

网格搜索的使用

---

本次网格搜索的数据集以手写识别数据集为例。

1. 获取数据，可以打印描述信息进行查看。

from sklearn.datasets import load_digits # 导入手写识别数据集
import numpy as np
from matplotlib import pyplot as plt

digits = load_digits()

X = digits.data
y = digits.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y)

2. 绘制出手写数字

x = X_train[1000].reshape(8, -1)
plt.imshow(x, cmap=plt.cm.binary)
plt.show()

3. 使用sklearn中的grid search

# 创建网格参数，每一组参数放在一个字典中
param_grid = [
    {'weights':['uniform'],
     'n_neighbors':[i for i in range(1,21)]
    },
    {
        'weights':['distance'],
        'n_neighbors': [i for i in range(1,21)],
        'p':[i for i in range(1,6)]
    }
] 

from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()

%%time
# 尝试寻找最佳参数
grid_search = GridSearchCV(knn_clf, param_grid, verbose=2, n_jobs=-1) # verbose越大越详细，n_jobs调用几个cpu进行计算，当n_jobs=-1时表示调用所有cpu进行计算
grid_search.fit(X_train, y_train)

grid_search.best_estimator_
grid_search.best_score_
grid_search.best_params_