2022 年牛客多校第十场补题记录

B Fall Guys-Perfect Match

题意：给定 $n\times n$ 的棋盘，每个格子有一个颜色 $a_{i,j}$，保证每种颜色出现次数不超过 $20$ 次。问站在哪个格子，到达任意一个格子的曼哈顿距离的最大值最小。$n\le 1\times 10^3$，颜色数目 $m\le n^2$。

解法：最大值最小，考虑二分答案。首先将曼哈顿距离 $|x|+|y|$ 转化为切比雪夫距离 $\max (|x|,|y|)$，则二分一个切比雪夫距离 $d$，考虑对首先枚举颜色，对于该颜色的全部格点向外侧扩张 $d$，取并集，那么二分所需要检查的条件为，每种颜色的矩形面积并的交（单个颜色内部并，之后再对每个颜色的面积并取交集）是否非空。

对于少量的矩形面积并（例如本题的 $20$ 个），可以直接对矩形的边进行离散化，然后暴力的染色填格子（只有 $20\times 20$ 个格子），然后再恢复回来即可，只需要用差分在总的方格上 $\mathcal{O}(k)$ 的修改即可计算出当前的矩形面积并。最后检查是否有格子被覆盖了 $m$ 次即可。总时间复杂度 $\mathcal{O}(n^2{k}^2\log n)$。

具体代码实现可以参看https://ac.nowcoder.com/acm/contest/view-submission?submissionId=53486593

D Mi Re Do Si La? So Fa!

题意：给定串 $S$，询问其每个子串的完整循环节长度和。例如串 aaaa的完整循环节长度有 $1,2,4$ 三种。$|S|\le 1\times 10^6$。

解法：显然每个子串 $S[l,r]$ 都有长度为 $r-l+1$ 的循环节。考虑循环节长度不为子串本身的循环节长度：

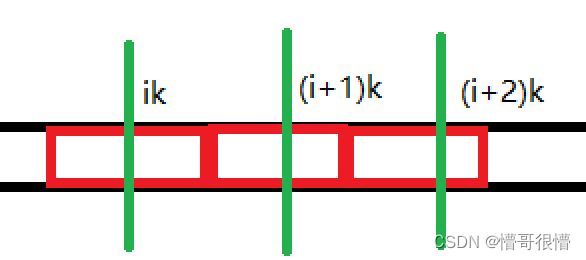
其中红色块代表长度为 $k$ 的循环节，那么如果串中存在子串有长度为 $k$ 的完整循环节，那么对于该串覆盖的任意的分段点（如上图中的 $ik,(i+1)k,(i+2)k$），则都有这若干处分段点开始（图中仅三处，可以更长）的总 $\mathrm{lcp}$ 长度与总 $\mathrm{lcs}$ 的长度和大于等于 $k$。

枚举长度 $k$ 再枚举分段点的位置 $ik$，设 $X$ 为 $ik$ 与 $(i+1)k$ 处的 $\mathrm{lcp}$ 长度，$Y$ 为 $ik$ 处与 $(i+1)k$ 的 $\mathrm{lcs}$ 长度，统计起始位置在 $((i-1)k,ik]$ 的所有子串，则满足完整循环节长度为 $k$ 的串个数等于从 $ik$ 处向前选择非空的一段、从 $ik$ 处再向后选择长度不超过 $Y$ 的一段，最终将两段拼接起来长度为 $k$ 的倍数的方案数，即求 $\sum _{i=1}^X\sum _{j=0}^Y[i+j\equiv 0(\mathrm{mod}k)]$，分类讨论即可。

最终总时间复杂度为 $\mathcal{O}(n{\log }^{2}n)$。

#include 
using namespace std;
const int N = 1'000'000;
int lg[N + 5];
class RMQ
{
    const int N = 20;
    vector<vector<int>> st;

public:
    void build(vector<int> &val)
    {
        st.resize(N + 1);
        int n = val.size() - 1;
        for (int i = 0; i <= N; i++)
            st[i].resize(n + 1);
        for (int i = 1; i <= n; i++)
            st[0][i] = val[i];
        for (int i = 1; i <= 20; i++)
            for (int j = 1; j + (1 << i) - 1 <= n; j++)
                st[i][j] = min(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
    }
    int query(int l, int r)
    {
        int X = lg[r - l + 1];
        return min(st[X][l], st[X][r - (1 << X) + 1]);
    }
};
class SA
{
    vector<int> rk, sa, cnt, height, oldrk, px, id;
    int n;
    bool cmp(int x, int y, int w)
    {
        return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
    }
    RMQ st;

public:
    void build(string s)
    {
        int n = s.length(), m = 300;
        this->n = n;
        oldrk.resize(max(m + 1, 2 * n + 1));
        sa.resize(max(m + 1, n + 1));
        rk.resize(max(m + 1, n + 1));
        cnt.resize(max(m + 1, n + 1));
        height.resize(max(m + 1, n + 1));
        px.resize(max(m + 1, n + 1));
        id.resize(max(m + 1, n + 1));
        s = " " + s;
        for (int i = 1; i <= n; ++i)
            ++cnt[rk[i] = s[i]];
        for (int i = 1; i <= m; ++i)
            cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i)
            sa[cnt[rk[i]]--] = i;
        for (int w = 1, p;; w <<= 1, m = p)
        {
            p = 0;
            for (int i = n; i > n - w; --i)
                id[++p] = i;
            for (int i = 1; i <= n; ++i)
                if (sa[i] > w)
                    id[++p] = sa[i] - w;
            fill(cnt.begin(), cnt.end(), 0);
            for (int i = 1; i <= n; ++i)
                ++cnt[px[i] = rk[id[i]]];
            for (int i = 1; i <= m; ++i)
                cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i)
                sa[cnt[px[i]]--] = id[i];
            copy(rk.begin(), rk.end(), oldrk.begin());
            p = 0;
            for (int i = 1; i <= n; ++i)
                rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
            if (p == n)
            {
                for (int i = 1; i <= n; ++i)
                    sa[rk[i]] = i;
                break;
            }
        }
        for (int i = 1, k = 0; i <= n; ++i)
        {
            if (rk[i] == 0)
                continue;
            if (k)
                --k;
            while (s[i + k] == s[sa[rk[i] - 1] + k])
                ++k;
            height[rk[i]] = k;
        }
        st.build(height);
    }
    int lcp(int x, int y)
    {
        if (x <= 0 || x > n || y <= 0 || y > n)
            return 0;
        int l = rk[x], r = rk[y];
        if (l > r)
            swap(l, r);
        return st.query(l + 1, r);
    }
};
class LongestCommon
{
    SA ord, rev;
    int n;

public:
    LongestCommon(string s)
    {
        this->n = s.length();
        ord.build(s);
        reverse(s.begin(), s.end());
        rev.build(s);
    }
    int lcp(int x, int y)
    {
        if (x <= 0 || x > n || y <= 0 || y > n)
            return 0;
        else
            return ord.lcp(x, y);
    }
    int lcs(int x, int y)
    {
        if (x <= 0 || x > n || y <= 0 || y > n)
            return 0;
        else
            return rev.lcp(n - x + 1, n - y + 1);
    }
};
int main()
{
    cin.tie(0)->sync_with_stdio(0);
    cin.exceptions(cin.failbit);
    cin.tie(NULL);
    cout.tie(NULL);
    for (int i = 2; i <= N; i++)
        lg[i] = lg[i >> 1] + 1;
    int t;
    string s;
    cin >> t;
    while (t--)
    {
        cin >> s;
        LongestCommon solve(s);
        int n = s.length();
        long long ans = 0;
        for (int i = 1; i <= n; i++)
        {
            ans += 1ll * i * (n - i + 1);
            for (int j = i; j + i <= n; j += i)
            {
                int suf = min(solve.lcs(j, j + i), i), pre = solve.lcp(j + 1, j + i + 1);
                long long s = 1ll * suf * (pre / i);
                pre %= i;
                if (suf == i)
                {
                    s++;
                    suf--;
                }
                int l = max(1, i - pre);
                if (l <= suf)
                    s += suf - l + 1;
                ans += s * i;
            }
        }
        cout << ans << "\n";
    }
    return 0;
}

E Reviewer Assignment

题意：有 $n$ 份论文，$m$ 个人每个人可以审稿这 $n$ 篇论文中的一些论文。找出一种方案，使得每个人只审核一篇论文的同时，设 $f_i$ 为至少被 $i$ 个人审核的论文数量，找到 $(f_1,f_2,\cdots ,f_n)$ 的字典序最大值。若有论文没人审核认为不合法。$n,m\le 400$。

解法：考虑费用流。源点 $S$ 向每个审稿人连接一条费用为 $0$，流量为 $1$ 的边，然后这些人向能审核的论文连接一条流量为 $1$，费用为 $0$ 的边。为了统计被审核次数的最小值，可以让每篇论文向汇点连接 $n$ 条边，流量均为 $1$，费用依次为 $1,2,\cdots ,n$。这样在总费用最小的时候，一定是让每篇论文都尽可能的被更多人审核——因为这样分配费用，保证了每个人都有论文看（保证总流量最大）的情况下，让一篇论文审核人数的更多的代价高于去审核一篇没多少人看的论文。或者在分配权值的时候，保证费用单调递增且严格凸即可，以达到上述目的。

#include 
#define fp(i, a, b) for (int i = a, i##_ = (b) + 1; i < i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = (b) - 1; i > i##_; --i)

using namespace std;
const int N = 405;
template <const int N, class Ty = int>
class MinCostMaxFlow {
    const Ty Inf = numeric_limits<Ty>::max();
    struct Edge {
        int v;
        Ty cap, cost;
        int rev;
    };
    Ty Sum{}, dis[N]{};
    int n{}, S{}, T{}, aug[N]{};
    bool Augment() {
        fill(dis, dis + n + 1, Inf);
        priority_queue<pair<int, int>> q;
        q.push({dis[T] = 0, T});
        for (int u, v; !q.empty() && q.top().first != Inf;) {
            u = q.top().second, q.pop();
            for (auto E : G[u])
                if (G[v = E.v][E.rev].cap && dis[v] > dis[u] - E.cost)
                    q.push({dis[v] = dis[u] - E.cost, v});
        }
        Sum += dis[S];
        for (int u = 1; u <= n; ++u)
            for (auto &E : G[u])
                E.cost += dis[E.v] - dis[u];
        return dis[S] != Inf;
    }
    Ty dfs(int u, Ty lim) {
        if (u == T)
            return Cost += lim * Sum, lim;
        Ty f = 0;
        int v;
        aug[u] = 1;
        for (auto &E : G[u])
            if (!E.cost && E.cap && !aug[v = E.v]) {
                int t = dfs(v, min(lim - f, E.cap));
                E.cap -= t, G[v][E.rev].cap += t, f += t;
                if (f == lim)
                    break;
            }
        if (f == lim)
            aug[u] = 0;
        return f;
    }

  public:
    vector<Edge> G[N];
    Ty Flow{}, Cost{};
    void Add(int u, int v, Ty a, Ty b) {
        G[u].push_back({v, a, b, (int)G[v].size()});
        G[v].push_back({u, 0, -b, (int)G[u].size() - 1});
    }
    pair<Ty, Ty> work(int _n, int _s, int _t) {
        Ty f;
        n = _n, S = _s, T = _t, Flow = Cost = 0;
        do
            do
                memset(aug, 0, (n + 1) << 2);
            while (Flow += (f = dfs(S, Inf)), f > 0);
        while (Augment());
        return {Flow, Cost};
    }
};
MinCostMaxFlow<N * N, int> D;
using ll = int64_t;
int n, m; char s[N];
void Solve() {
    scanf("%d%d", &n, &m);
    int S = n + m + 1, T = S + 1;
    fp(i, 1, n) {
        D.Add(S, i, 1, 0);
        scanf("%s", s + 1);
        fp(j, 1, m) if (s[j] == '1')
            D.Add(i, n + j, 1, 0);
    }
    fp(i, 1, m)
        fp(j, 1, n)
            D.Add(n + i, T, 1, j);
    auto f = D.work(T, S, T);
    if (f.first != n)
        return puts("-1"), void();
    fp(i, 1, n) {
        for (auto e : D.G[i])
            if (!e.cap && e.v > n) {
                printf("%d ", e.v - n);
                break;
            }
    }
}
int main() {
    int t = 1;
    while (t--) Solve();
    return 0;
}

F Shannon Switching Game?

题意：给定一个多重无向图 $G(V,E)$ 和一对点 $s,t$，起始时 $s$ 处有一个令牌。先手可以选择删除图上的一条边，后手可以选择删除令牌所在点 $u$ 邻接的一条边 $(u,v)$，然后将令牌移动到 $v$。当令牌移动到 $t$ 时后手获胜，否则先手胜。问最终结局。$|V|\le 100,|E|\le 1\times 10^3$。

解法：若令牌所处的位置确定，则胜负已分。显然若令牌在 $t$ 处为一个必胜态，若某个节点能到达两个及以上的必胜态，则该节点也为必胜态——因为先手没办法删完该点通向必胜态的边。所以倒过来从 $t$ 开始 bfs 找必胜态节点即可。总时间复杂度 $\mathcal{O}(|V|+|E|)$。

#include 
using namespace std;
int main()
{
    int caset, n, m, s, t;
    scanf("%d", &caset);
    while (caset--)
    {
        scanf("%d%d%d%d", &n, &m, &s, &t);
        vector<vector<int>> deg(n + 1, vector<int>(n + 1, 0));
        vector<vector<int>> g(n + 1);
        for (int i = 1, u, v; i <= m; i++)
        {
            scanf("%d%d", &u, &v);
            deg[u][v]++;
            deg[v][u]++;
            g[u].push_back(v);
            g[v].push_back(u);
        }
        vector<int> vis(n + 1), in(n + 1, 0);
        queue<int> q;
        vis[t] = 1;
        q.push(t);
        while (!q.empty())
        {
            int tp = q.front();
            q.pop();
            for (auto i : g[tp])
            {
                if (deg[tp][i] > 1)
                {
                    if (!vis[i] && vis[tp])
                    {
                        vis[i] = 1;
                        q.push(i);
                    }
                }
                else if (deg[tp][i] == 1 && vis[tp])
                    in[i]++;
                if (in[i] >= 2 && !vis[i])
                {
                    vis[i] = 1;
                    q.push(i);
                }
            }
        }
        if (vis[s])
            printf("Join Player\n");
        else
            printf("Cut Player\n");
    }
    return 0;
}

G Steins’ Game 2

题意：有 $n$ 堆石子 $\{a_n\}$，满足 $0\le a_1\le a_2\cdots \le a_n\le m$。Alice 与 Bob 依次从非空的一堆拿走正数个石子使得每堆石子的石子个数仍然是非递减的。求有多少种合法的石子分配方案使得 Bob 必胜。$n\le 4\times 10^4$，$m\le 1\times 10^{12}$。

解法：考虑 $\{a_n\}$ 的差分数组 $\{b_n\}$，则该问题与 $\{b_n\}$ 序列构成的阶梯 Nim（有 $n$ 堆石子，每次可以从第 $i$ 堆的石子中拿走一部分放到第 $i-1$ 堆中，或者把第 $1$ 堆中的石子拿走一部分，无法操作者算输）是完全等价的。考虑 Bob 获胜条件，利用阶梯 Nim 的必胜条件：奇数堆石子的异或值为 $0$。得到这题的转化题意：前 $k=\lceil \frac{n}{2}\rceil$ 个石子异或值为 $0$，$\sum b_i=m$ 的方案数。这是因为如果有奇数堆石子，则最后新添加一堆石子不会影响阶梯 Nim 的性质，这时不妨在 $\{a_n\}$ 的末尾添加一堆石子数为 $m$ 的石子；若原来有偶数堆石子，也可以在 $\{a_n\}$ 的最后增补两堆均为 $m$ 的石子，此时对于 $\{b_n\}$ 序列只是增加了一个 $0$。则该转化将 $\{b_n\}$ 中奇数堆石子移动到最前面，变成前缀异或和，且忽略了 $\{b_n\}$ 中每个数字的大小关系。

考虑每一个数字的每一个 bit 位上填 $0,1$ 的方案。对于 $2^k$ 这一 bit，要求前缀 $k$ 的异或和为 $0$ 的的生成函数为 $f(x)=\sum _{i=0}^k[i\mathrm{mod}2=0]\left(\genfrac{}{}{0ex}{}{k}{i}\right)x^i$，即仅能选择偶数个数字填 $1$，并且进行选择。对于剩余的 $n-k$ 个数字，可以任选，其方案为 $g(x)=(1+x{)}^{n-k}$，因而整层的填法方案的生成函数为 $h(x)=f(x)g(x)$。不难发现，对于每一层的填法均相同，因而可以预处理。

接下来考虑背包的容量。这一处理与 2022 年牛客第一场的 H 题是完全一样的：$f_{i,j}$ 表示填完低 $i$ 个 bit，最后剩余 $j{2}^i$ 的容量的方案数。则转移是显然的：$f_{i+1,j}=\sum _{k=0}^l{f}_{i,k}[x^{l-k}]h(x)$，其中 $l=2j+{\mathrm{bit}}_i$ 表示当前位的最大容量。注意到这个 $j\le 2n$（更大了则完全填不上），因而只需要保留 $2n$ 项即可。

总时间复杂度 $\mathcal{O}(n\log n\log m)$。

int main()
{
    int n;
    long long m;
    scanf("%d%lld", &n, &m);
    Poly a, b;
    if (n % 2 == 0)
    {
        int k = n / 2 + 1;
        b.resize(k + 1);
        a.resize(n / 2 + 1);
        for (int i = 0; i <= k; i++)
            b[i] = C(k, i);
        for (int i = 0; i <= n / 2; i += 2)
            a[i] = C(n / 2, i);
    }
    else
    {
        int k = (n + 1) / 2;
        b.resize(k + 1), a.resize(k + 1);
        for (int i = 0; i <= k; i++)
            b[i] = C(k, i);
        for (int i = 0; i <= k; i += 2)
            if (i % 2 == 0)
                a[i] = C(k, i);
    }
    auto way = a * b;
    vector<int> digit;
    long long x = m;
    while (x)
    {
        digit.push_back(x & 1);
        x >>= 1;
    }
    f[0][0] = 1;
    for (int k = 1; k <= digit.size(); k++)
    {
        Poly cur(2 * n + 5);
        for (int i = 0; i <= n + 1;i++)
            cur[i] = f[k - 1][i];
        cur = cur * way;
        for (int i = 0; i <= n + 1;i++)
            f[k][i] = cur[i * 2 + digit[k - 1]];
    }
    printf("%lld", f[digit.size()][0]);
    return 0;
}

H Wheel of Fortune

题意：给定 $16$ 个数字 $A,B,a_1,a_2,\cdots ,a_7,b_1,b_2,\cdots ,b_7$，从中随机选择一个数字 $x$ 使得 $x\leftarrow x-10$，直到 $A\le 0$ 或者 $B\le 0$。问有多大概率 $B\le 0$ 的结束游戏。

解法：显然随机选择数字只和 $A,B$ 有关。记 $x=\lceil \frac{A}{10}\rceil$，$y=\lceil \frac{B}{10}\rceil$，则只需要让 $B$ 被选择 $y$ 次之前 $A$ 不被选择到 $x$ 次即可，且最后一击必须是抽中 $B$。答案为 $\sum _{i=0}^{x-1}\left(\genfrac{}{}{0ex}{}{i+y-1}{i}\right)2^{-(i+y)}$。

I Yet Another FFT Problem?

题意：给定长度分别为 $n,m$ 的序列 $\{a_n\},\{b_m\}$，问是否存在四个下标 $i,j,k,l$ 满足 $1\le i\le j\le n,1\le k\le l\le m$ 且 $|a_i-a_j|=|b_k-b_l|$。$a_i,b_i\le 1\times 10^7$，$n,m\le 1\times 10^6$。

解法：不妨减少限制 $i\le j$ 和 $k\le l$，则可脱去绝对值有 $a_i-a_j=b_k-b_l$，即 $a_i+b_l=a_j+b_k$。那么问题转化为，从 $\{a_n\},\{b_m\}$ 中分别选一个数使得他们碰撞。由于 $a_i,b_i\le 1\times 10^7$，则 $a_i+b_j\in [1,2\times 10^7]$，因而用鸽巢原理可得，$\{b\}$ 序列长度不超过 $\lceil \frac{2\times 10^7}{n}\rceil$ 就必然产生碰撞。所以仅需要保留 $b$ 序列的前 $\lceil \frac{2\times 10^7}{n}\rceil$ 项即可。总时间复杂度 $O(V)$，其中 $V$ 代表 $a,b$ 的值域。

#include 
#define fp(i, a, b) for (int i = a, i##_ = (b) + 1; i < i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = (b) - 1; i > i##_; --i)

using namespace std;
const int N = 2e7 + 5;
using pii = pair<int, int>;
int n, m;
pii w[N];
unordered_map<int, vector<int>> A, B;
void Solve() {   
    scanf("%d%d", &n, &m);
    for (int x, i = 1; i <= n; ++i) scanf("%d", &x), A[x].push_back(i);
    for (int x, i = 1; i <= m; ++i) scanf("%d", &x), B[x].push_back(i);
    vector<pii> a, b;
    pii ma, mb;
    for (auto &[i, v] : A) {
        a.push_back({i, v[0]});
        if (v.size() > 1) ma = {v[0], v[1]};
    }
    for (auto &[i, v] : B) {
        b.push_back({i, v[0]});
        if (v.size() > 1) mb = {v[0], v[1]};
    }
    if (ma.first && mb.first)
        return printf("%d %d %d %d\n", ma.first, ma.second, mb.first, mb.second), void();
    b.resize(min(b.size(), size_t(2e7 / a.size())));
    for (auto &[x, i] : a)
        for (auto &[y, k] : b) {
        auto [j, l] = w[x + y];
        if (j && i != j && k != l) {
            printf("%d %d %d %d\n", i, j, k, l);
            return;
        } else w[x + y] = {i, k};
    }
    puts("-1");
}
int main() {
    int t = 1;
    while (t--) Solve();
    return 0;
}

K You are given a tree…

题意：给定一个 $n$ 个节点的树，树上每个点有颜色 $a_i$，边有边权。问从中选择 $k$ 个颜色不同的点，他们构成的生成子图的边权值和最大值。$n\le 1\times 10^3$，$k\in [2,5]$，$a_i\le 1\times 10^9$。

解法：若颜色种类非常少（小于等于 $10$），可以直接使用状压 dp：$f_{u,S}$ 表示在子树 $u$ 内选择了颜色集合为 $S$ 的最大边权值和，枚举子集，使用子树合并，则有：
$$f_{u,S}\leftarrow f_{u,S/T}+f_{v,T}+[a_u\in S\cap a_v\in T]w_{u,v}$$
这样的时间复杂度为 $\mathcal{O}(n{3}^k)$。

但是本题的颜色范围过大，而 $k$ 又非常小，因而大部分颜色其实根本用不到选不了，因而可以当成同一种颜色看待。可以考虑使用随机化，把所有的颜色归入到 $k$ 类中，然后使用上述树形 dp 求解得到答案。若颜色种类有 $m$ 种（$m\ge k$），则正确概率可以估计为 $p=\frac{1}{\left(\genfrac{}{}{0ex}{}{m}{k}\right)}$，随机 $200$ 次正确概率已经相当大了。

因而总的时间复杂度为 $\mathcal{O}(Tn{3}^k)$。

#include 
using namespace std;
const int N = 5000;
struct line
{
    int from, to;
    long long v;
    int next;
};
struct line que[2 * N + 5];
int cnt, headers[N + 5];
void add(int from, int to, long long v)
{
    cnt++;
    que[cnt].from = from;
    que[cnt].to = to;
    que[cnt].v = v;
    que[cnt].next = headers[from];
    headers[from] = cnt;
}
long long f[N + 5][1 << 5];
int a[N + 5], col[N + 5], n, k;
long long ans;
void dfs(int place, int father)
{
    f[place][0] = f[place][1 << col[a[place]]] = 0;
    for (int i = headers[place]; i; i = que[i].next)
        if (que[i].to != father)
        {
            dfs(que[i].to, place);
            for (int S = 1; S < 1 << k;S++)
                f[que[i].to][S] += que[i].v;
            for (int S = (1 << k) - 1; S >= 0; S--)
            {
                for (int T = S; T; T = (T - 1) & S)
                {
                    f[place][S] = max(f[place][S], f[place][S ^ T] + f[que[i].to][T]);
                    if (S ^ T)
                        ans = max(ans, f[place][S ^ T] + f[que[i].to][T]);
                }
            }
        }
}
int main()
{
    unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
    mt19937 rand_num(seed);
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n;i++)
        scanf("%d", &a[i]);
    uniform_int_distribution<int> dist(0, k - 1);
    for (int i = 1, u, v, w; i < n; i++)
    {
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);
        add(v, u, w);
    }
    long long res = 0;
    for (int times = 1; times <= 200; times++)
    {
        memset(f, 0xcf, sizeof(f));
        ans = 0;
        for (int i = 1; i <= n; i++)
            col[i] = dist(rand_num);
        dfs(1, 1);
        res = max(res, ans);
    }
    printf("%lld", res);
    return 0;
}