2.相机的畸变介绍

2.相机的畸变介绍

畸变是指光学系统对物体所成的像相对于物体本身而言的失真程度，是光学透镜的固有特性，其直接原因是因为透镜的边缘部分和中心部分的放大倍率不一样。
透镜的畸变是不可消除的，但在实际的应用中可以通过一些软件来进行畸变的补偿，如OpenCV、MATLAB等。
相机的畸变主要分为以下几类：

• 径向畸变：主要由于透镜不同部位放大倍率不同造成的，又分枕型畸变，桶形畸变两种
• 切向畸变：主要由于透镜安装与成像平面不垂直造成的，类似透视原理（近大远小，圆变椭圆等等）
• 薄棱镜畸变：由于透镜设计缺陷和加工安装误差造成，又称为线性畸变。影响较小，一般忽略不计

通常情况下径向畸变的影响要远远大于其他畸变，因此由Brown在《Close-Range Camera Celibration》一文中所提及的径向畸变模型和切向畸变模型应用比较广泛。

2.1畸变模型

如下为Brown在论文中提及的径向畸变和切向畸变模型：
径向畸变模型：
$$\{\begin{array}{c}{x}^{\prime }=x+\overline{x}(k_1{r}^2+k_2{r}^4+k_3{r}^6)\\ y^{\prime }=y+\overline{y}(k_1{r}^2+k_2{r}^4+k_3{r}^6)\end{array}$$切向畸变模型：
$$\{\begin{array}{c}{x}^{\prime }=x+p_1(r^2+2{\overline{x}}^2)+2p_2\overline{x}\ast \overline{y}\\ y^{\prime }=y+p_2(r^2+2{\overline{y}}^2)+2p_1\overline{x}\ast \overline{y}\end{array}$$径向加切向畸变模型：
$$\{\begin{array}{c}{x}^{\prime }=x+\overline{x}(k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2{\overline{x}}^2)+2p_2\overline{x}\ast \overline{y}\\ y^{\prime }=y+\overline{y}(k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_2(r^2+2{\overline{y}}^2)+2p_1\overline{x}\ast \overline{y}\end{array}$$该畸变模型中$(x^{\prime },y^{\prime })$为二次畸变的坐标，$(x,y)$为一次畸变（未校正前的图像下的）坐标。

这里谁是畸变坐标，谁是理想坐标，真的是搞晕了。
论文原文中描述为：
However,if the coordinates x,y of points on the image of a plumb line were corrected for such distortion, ther would conform to a straight line.
译文：然而，如果这个铅垂线的图像上的点的坐标(x,y)被校正过这种失真，它们将符合一条直线。
这在$(x,y)$为畸变坐标还是理想坐标的概念上有些模糊。
在《最详细、最完整的相机标定讲解》链接一文中有明确指出$(x^{\prime },y^{\prime })$为理想坐标，$(x,y)$为实际坐标。在论文《数码相机畸变模型的相互转换方法》-任超峰 中，作者称$(x,y)$为原始像点，$(x^{\prime },y^{\prime })$为理论像点。
但是好多文章里也会讲到，$(x^{\prime },y^{\prime })$为实际坐标，$(x,y)$为理想坐标。如在《相机参数标定》链接一文中就有明确指出。
笔者这里认为$(x^{\prime },y^{\prime })$为产生了畸变的坐标，$(x,y)$为理想状态下的坐标。
这与下述的OpenCV的畸变模型能够产生对照，可信度更大。
(实践是检验真理的唯一标准，在条件允许的情况下，大家可以通过OpenCV来验证一下。欢迎讨论)
**> 2021/12/3日对该处进行补充：
畸变模型是对真实物体的二次畸变，准确来说，透过镜头得到的图像（桶形畸变等）称为一次畸变，之后通过畸变模型进行调整称为二次畸变。即准确来说$(x^{\prime },y^{\prime })$为二次畸变后的坐标，$(x,y)$为一次畸变后的坐标。**这里可以参考《计算机视觉——算法与应用》第46页2.1.6<镜头畸变>中的说法

$$\begin{gathered} \overline{x}=x-x_p \\ \overline{y}=y-y_p \end{gathered}$$$$r^2={\overline{x}}^2+{\overline{y}}^2=(x-x_p{)}^2+(y-y_p{)}^2$$

由于该公式是根据Brown在1964,1965两年发表的文章进行修正的，所以式中的$(x_p,y_p)$的具体含义在原文中并没有过多赘述。但这两篇文章笔者也没能够找到原文。
这里附上这两篇文章的名字《An Advanced Plate Reduction for Photogrammetric Cameras》、《Decentering Distortion of Lenses》
读者有兴趣可以查找一下

查阅论文《数码相机畸变模型的相互转换方法》-任超峰。确定$(x_p,y_p)$为相机的内方位元素。

内方位元素是描述摄影中心与图像平面之间相互位置关系的元素，主要包含焦距$f$，以及$(x_p,y_p)$
$(x_p,y_p)$为像主点在图像坐标系中的坐标，像主点为图像的中心点，理论上应当通过相机光轴。
即实际的图像坐标系和理论上的图像坐标系之间由于制造或者安装的缘故，使二者之间产生了$(x_p,y_p)$的偏差。
内方位元素一般视为已知的，可以通过对相机的鉴定的得到

通常情况下，对于数码影像，其内方位元素可以视为$(x_p,y_p)=(0,0)$
因此，我们通常看到的畸变模型为如下形式：
$$\{\begin{array}{c}{x}^{\prime }=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2x^2)+2p_{2}xy\\ y^{\prime }=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_2(r^2+2y^2)+2p_{1}xy\end{array}$$

2.2像方畸变和物方畸变

• 像方畸变模型：即将畸变模型作为附属参数添加至图像平面。通俗的来讲就是认为，图像透过透镜之前是正常的(理想的)，透过透镜后，在图像平面成像时产生了畸变。
• 物方畸变模型：即将畸变模型作为附属参数添加至相机坐标系。通俗的讲就是认为，图像从进入相机开始就已经产生了畸变，之后这种畸变一直保持存在。

像方畸变模型和物方畸变模型都是对图像的校正模型，只是采取的参考系不同而已。

• Inpho等传统摄影测量软件通常情况下都是采用像方畸变模型
• OpenCV、Matlab等计算机视觉软件通常采用物方畸变模型

2.3OpenCV畸变模型

OpenCV采用了物方畸变模型，对相机坐标系下的坐标进行畸变模型处理
在OpenCV官网文件中有对畸变模型的详细介绍链接

​上篇文章中讲到，一点X，其在世界坐标系中的坐标为：$(x_w,y_w,z_w)$
​其在相机坐标系中的坐标为：$(X_c,Y_c,Z_c)$
​其在图像坐标系中的坐标为：$(x_i,y_i)$
​其在像素坐标系中的坐标为：$(P_{x_i},P_{y_i})$
世界坐标系到像素坐标系的坐标转换矩阵：
$$\left[\begin{array}{c}{P}_{x_i}\ast Z_c\\ P_{y_i}\ast Z_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}M\ast f& 0& M\ast P_x\\ 0& N\ast f& N\ast P_y\\ 0& 0& 1\end{array}\right]\ast (R|-Rc)\ast \left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$将其中的坐标带入到OpenCV中转换坐标中：$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\ast \left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]+C$$
对相机坐标系的坐标进行处理：
$$\{\begin{array}{c}{x}^{\prime }=X_c/Z_c\\ y^{\prime }=Y_x/Z_c\end{array}$$将处理后的坐标带入到畸变模型中，(公式有些复杂，上图吧)

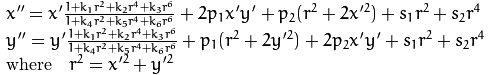
然后转化到图像坐标系
$$\{\begin{array}{c}{x}_i^{\prime }=x^{\prime \prime }\ast f\\ y_i^{\prime }=y^{\prime \prime }\ast f\end{array}$$再转化到像素坐标系进行单位转换
$$\{\begin{array}{c}{P}_{x_i}^{\prime }=x_i^{\prime }+P_x\\ P_{y_i}^{\prime }=y_i^{\prime }+P_y\end{array}$$进行单位转换
$$\{\begin{array}{c}{P}_{x_i}^{\prime }=M{x}_i^{\prime }+M{P}_x\\ P_{y_i}^{\prime }=N{y}_i^{\prime }+N{P}_y\end{array}$$
式中$k_1,k_2,k_3,k_4,k_5,k_6$是径向畸变系数。$p_1,p_2$为切向畸变系数。薄棱镜畸变不考虑。
容易知道，OpenCV是将畸变模型加在相机坐标系下，因此属于物方畸变模型
将加入畸变模型后的转换过程整理为矩阵形式如下，整体上来看和理想状态下的坐标转换矩阵相似：
$$\left[\begin{array}{c}{P}_{x_i}^{\prime }\\ P_{y_i}^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}M\ast f& 0& M\ast P_x\\ 0& N\ast f& N\ast P_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}^{\prime \prime }\\ y^{\prime \prime }\\ 1\end{array}\right]$$