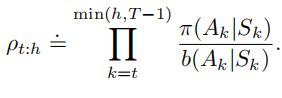【强化学习】n步Bootstrapping

目录

n步TD 预测

n-step Sarsa

n步off - policy学习

Per-reward Off - policy 方法

n步Tree Backup算法

---

BootStrapping原是推论统计学里的概念。所谓推论统计学，就是根据样本统计量来推算总体的统计量。n部方法通常会被用作eligibility trace思想的一个例子，这个思想允许BootStrapping在多个时间段同时开展操作。n 步BootStrapping的性能一般要比MC方法和TD方法要好。

n步TD 预测

TD(0)实际上是1步TD算法，之所以是“1”，是因为它只需要计算1个后继行为和1个后继状态来更新当前状态。以此类推，当计算了n个后继行为及n个后继状态来更新当前状态时，则为n步TD预测。当时，即为MC算法。如下图所示：

考虑根据“状态-收益”序列（省略行为A）来更新的价值。在MC算法中，价值，的估计会沿着一条完整的episode进行更新：

其中，是终止状态的时刻。在TD(0)中，累计收益是即时收益加上后继状态的价值函数估计值乘以折扣系数，称其为单步回报：

的下标表示一种截断回报，由当前时刻到时刻的累积收益和折后回报组成，这种想法扩展到两步的情况为两步回报：

类似地，任意n步更新的目标是n步回报

 n步回报可以看做是一个完整episode回报的近似，上式第n步（不包含n）以后的其余部分用来替代。如果（即n步回报超出了终止状态），则其余部分的值都为0。基于n步回报的状态价值函数更新算法是：

在更新时，其他状态的价值估计保持不变：，这个算法被称为n步时序差分（n步TD）算法。 

 n步TD算法伪代码如下：

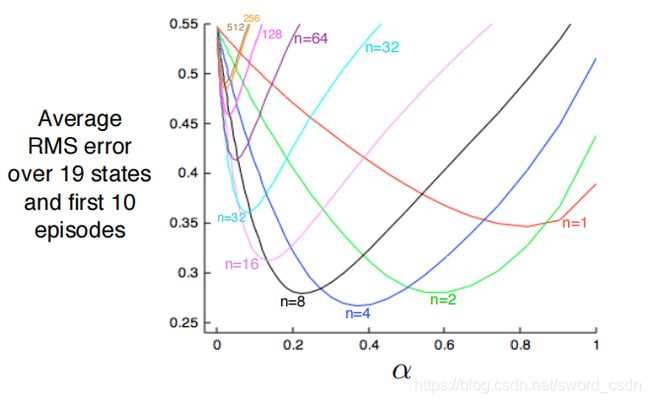
不同的，比较

n-step Sarsa

该方法的核心思想是将状态替换为“状态-动作”二元组，然后使用-贪心策略。n Sarsa的回溯图和n TD的回溯图类似，都是由交替出现的状态和动作构成。唯一不同的是Sarsa的回溯图首末两端都是动作而不是状态。根据动作的价值估计定义n-step方法的回报如下：

当时，。基于此，会得到算法

除了上面更新的状态之外，所有其他状态的价值都保持不变，即对于所有满足或的，来说，，这就是n步Sarsa算法。

n步off - policy学习

off - policy使用策略来学习策略，需要考虑两个策略、的不同，所以需要使用相对概率。由于方法中，回报根据n步来建立，所以需要考虑n步的相对概率。例如实现一个简单off-policy版本的n步TD学习，对于时刻状态价值的更新，可以用来加权。

其中是重要度采样率，是两种策略采取这个动作的相对概率。

假设策略永远不会采取某个特定动作，即，则n步回报的权重为0，即完全忽略。另一方面，如何策略采取某个动作的概率很大，则这个权重也会增加。所以n步Sarsa更新方法的off - policy版如下：

off - policy n - step Sarsa方法如下： 

Per-reward Off - policy 方法

对于普通n步方法的回报，像所有回报一样，可以写成递归方式。

然后考虑off - policy的影响（不同的策略，目标策略和行为策略而产生的影响），对于t时刻的第一次收益和下一个状态都必须用重要度采样率加权，除了可以对上式等号右侧直接加权之外，还有更好的方法，就是加多一项，这一项被称为控制变量。最后该n步回报的off - policy策略可以定义成：

在这个方法中，如果,则它不会使得目标为0并导致估计值收缩，而是使得目标和估计值一样，因而不会带来任何变化。重要度采样率为0意味着忽略样本，所以让估计值保持不变是合理的。

n步Tree Backup算法

如下图所示：

包含两个采样动作和，在MC，TD中，这个图就是一条分支，直到终止状态。不同点在于这里只采样有限步，用估计的价值函数替代后续的采样回报（BootStrapping）。这里有采样，但是也包含没有采样到的动作价值函数（图中的左右节点）。没有采样到的动作节点叫做叶子节点。（所谓叶子节点就是没有子节点的节点，在状态的时候，一个动作都没选择，对应它的子节点都是叶子节点）

目标更新

一般情况下，会使用实际采样的序列这条分支（中间）来构造更新的目标。但是在tree backup更新中，不仅包含采样的动作序列，还需要考虑旁边的动作。类似于从叶子节点到根节点的一次回溯，叫做tree backup。

更新目标（父节点）是通过叶子节点的价值函数构造。这里首先给每一个叶子节点分配一个权重。这个权重是叶子节点对应动作在目标策略下的概率。而更新时，就是以此概率作为权重的，所有的叶子节点的加权之和。对于第一层的叶子节点（下面的两个叶子节点），权重是。而对于该层的非叶子节点，也就是，它发生的概率用来给所有第2层的节点加权，以此类推。

对于每个叶子节点以及他们的加权权重如上图所示。对于单步tree backup算法，其回报与Expected Sarsa算法相同。对于，有

对于，也就是2步tree backup 算法，它的回报是

对于tree backup算法的n步回报的地柜定义的一般形式。即对于，有

n步tree backup算法的伪代码如下：