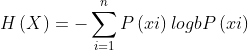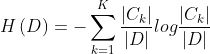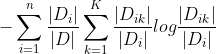机器学习入门(3、分类算法)
1、分类算法
1-1 KNN(K Nearest Neighbor)算法
1-2 模型选择与调优
1、什么是交叉验证(Cross Validation)?
2、超参数搜索—网格搜索(Grid Search)
1-3 朴素贝叶斯算法
怎么避免分子出现0的情况?
1-4 决策树
1-5 随机森林
什么是集成学习法?
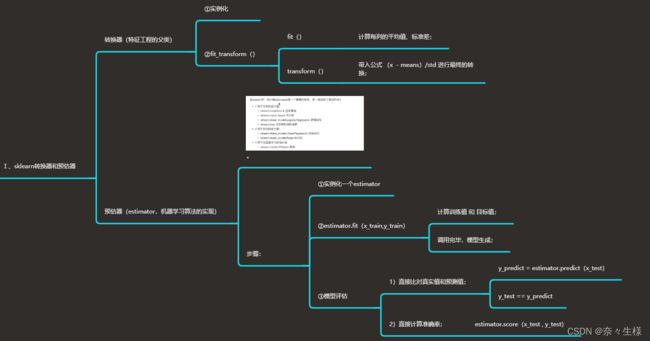
有监督的学习算法包含预测 和 分类 两种,预测是对连续型数值进行计算的算法,分类 是对阈值内外数值进行判断的分类器算法。
在sklearn中算法的实现,通过 转换器(fit_transform() ) 和 预估器(estimator() ) 来进行实现。
1、分类算法
1-1 KNN(K Nearest Neighbor)算法
核心思想:通过你的“邻居”推断你的类别。
如何确定“邻居”?通过计算距离来判断,而计算距离主要有以下方式:
①欧式距离(常用):![]()
②曼哈顿距离:![]()
③明可夫斯基距离:![]()
由上述公式可明了,明可夫斯基距离是欧式和曼哈顿距离的推广,当 p = 2 时,是欧氏距离;当 p =1 时,是曼哈顿距离。
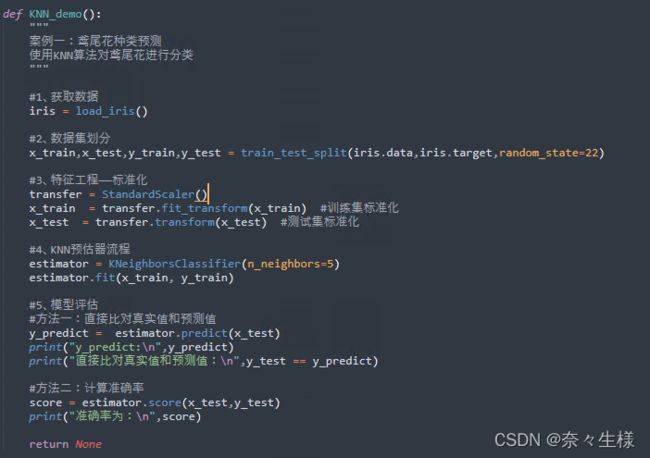
以下是KNN算法的 sklearn 实现,需 import sklearn.neighbors.KNeighborsClassfier ,其中n_neighbors = 参数,是用来设定计算的邻居数;
KNN算法简单、易于理解,但K的取值比较重要,K = 1,容易受到异常值的影响;K取值过大,在样本不均衡时容易受到影响。性能方面,KNN是懒惰算法,计算量大,内存开销大。
1-2 模型选择与调优
1、什么是交叉验证(Cross Validation)?
将拿到的训练数据,分为训练和验证集。将数据分成4份,其中一份作为验证集。然后经过4次(组)的测试,每次都更换不同的验证集。即得到4组模型的结果,取平均值作为最终结果,又称4折交叉验证。
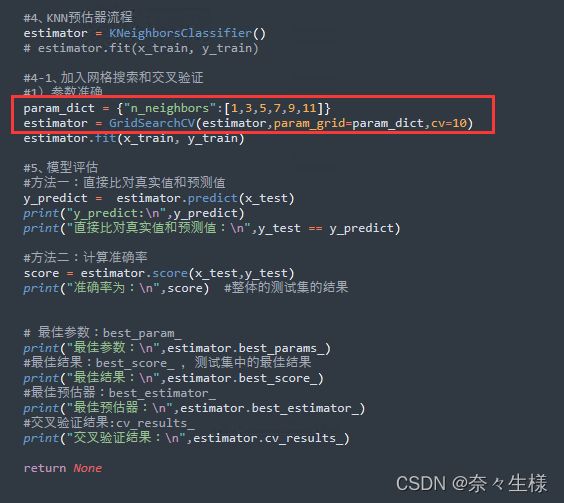
2、超参数搜索—网格搜索(Grid Search)
需要手动指定的这类参数,叫做超参数(例如:KNN算法中 K 的取值)。搜索手段类似暴力破解,通过遍历的方式,来找出最优解。
以下是 sklearn 中的调用,需要import sklearn.model_selection.GridSearchCV ,其中 cv = 参数的取值,一般制定为 10(十折交叉验证) ,若数据量很大,可适当减小。
1-3 朴素贝叶斯算法
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
朴素(假定特征与特征相互独立)+贝叶斯(贝叶斯公式),经常应用在文本分类(以单词作为特征)。
(W为给定文档的特征值(频数统计,预测文档提供),C为文档类别,
p(b|a)条件概率、p(a,b)联合概率)
怎么避免分子出现0的情况?
(α为指定的系数一般为1,m为训练文档中统计出的特征词个数)
在 sklearn中的实现,需 import sklearn.navie_bayes.MultinomialNB( alpha = 1.0),其中alpha 即拉普拉斯平滑系数。
1-4 决策树
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
决策树算法旨在通过确定特征判断的先后顺序,来达到高效决策的目的。划分依据:信息熵、信息增益。
信息增益: ![]()
(特征A对训练集D的信息增益g(D,A),定义为集合D的信息熵与特征A给定条件下D的信息
条件熵H(D|A)之差)
决策树的其他方法,原理都类似,还包括 ID3(信息增益最大的准则)、C4.5(信息增益比最大的的准则)、CART(分类书树:gini系数最小准则,sklearn的默认原则,划分更加细致)
以上是sklearn的实现,需 import sklearn.tree.DecisionTreeClassfiier 调用。
决策树能够进行可视化(sklearn.tree.export_graphviz),可解释能力强,但是可能会创建不能很好推广、数据过于复杂的树,容易过拟合。(改进:①剪枝;②随机森林算法)
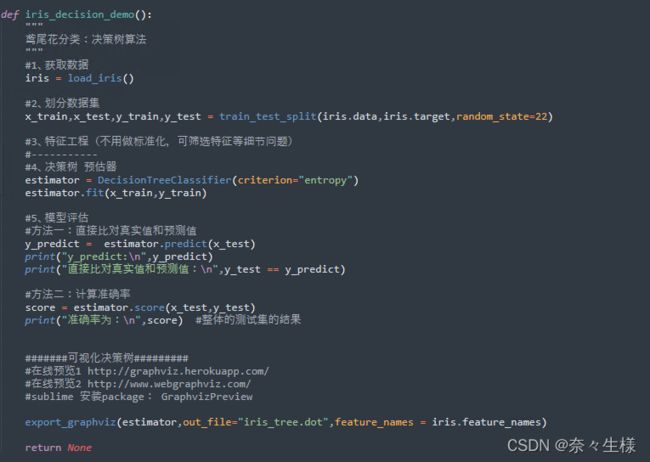
1-5 随机森林
什么是集成学习法?
通过建立几个模型组合来解决单一预测问题,原理是生成多个分类器/模型,各自独立的学习和作出预测,这些预测最后结合成组合预测,因此优于任何一个单分类的作出预测。
随机森林是一个包含了多个决策树的分类器,森林即多个决策树,有两个随机:
①特征值随机:从 M 个特征中随机抽取 m 个特征( M >> m,有降维的效果 );
②训练集随机:从 N 个样本中随机有放回的抽取 N 个样本;
以下是sklearn 在泰坦尼克号生存预测中的调用随机森林算法的示例,需 import sklearn.ensenble.RandomForestClassfier ,可使用n_estimators = 参数来设置森林里的树木数量,max_depth = 参数来设置树的最大深度。
总结:随机森林算法,能够有效的运行在大数据集上,处理具有高维特征的输入样本,而且不需要降维。