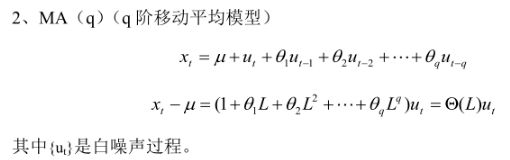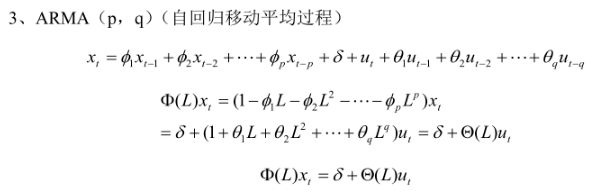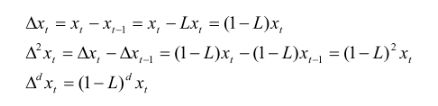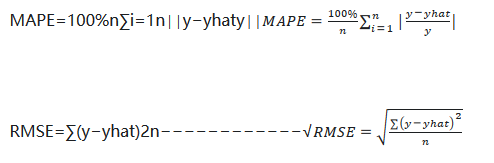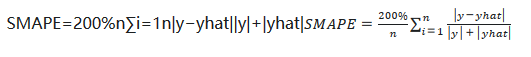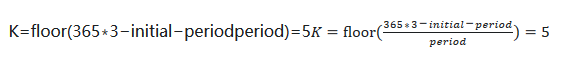【机器学习】时序预测Arima & HoltWinters算法及评估方法 整理
时序预测(Arima 和 HoltWinters)算法 及 评估方法 整理。spark 库里没有 Spark TimeSeries 时序预测算法,但是国外有人已经写好了相应的算法。https://github.com/sryza/spark-timeseries
时间序列分析
时间序列,就是按时间顺序排列的,随时间变化的数据序列。
生活中各领域各行业太多时间序列的数据了,销售额,顾客数,访问量,股价,油价,GDP,气温。。。
随机过程的特征有均值、方差、协方差等。
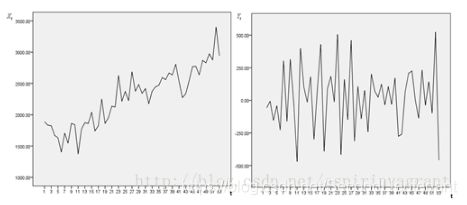
如果随机过程的特征随着时间变化,则此过程是非平稳的;相反,如果随机过程的特征不随时间而变化,就称此过程是平稳的。
下图所示,左边非稳定,右边稳定。
非平稳时间序列分析时,若导致非平稳的原因是确定的,可以用的方法主要有趋势拟合模型、季节调整模型、移动平均、指数平滑等方法。
若导致非平稳的原因是随机的,方法主要有ARIMA(autoregressive integrated moving average)及自回归条件异方差模型等。
ARIMA
ARIMA (Auto Regressive Integrated Moving Average) 可以用来对时间序列进行预测,常被用于需求预测和规划中。
可以用来对付 ‘随机过程的特征随着时间变化而非固定’ 且 ‘导致时间序列非平稳的原因是随机而非确定’ 的问题。不过,如果是从一个非平稳的时间序列开始, 首先需要做差分,直到得到一个平稳的序列。
模型的思想,是从历史的数据中学习到随时间变化的模式,学到了就用这个规律去预测未来。
ARIMA数学模型
ARIMA(p,d,q)模型是ARMA(p,q)模型的扩展。
ARIMA(p,d,q)模型可以表示为:
其中:d 是差分的阶数,用来得到平稳序列;p为AR自回归项的系数;q为MA移动平均项的系数。
L 是滞后算子(Lag operator),d in Z, d>0。
AR:当前值只是过去值的加权求和。
MA:过去的白噪音的移动平均。
ARMA:AR和MA的综合。
ARIMA:和ARMA的区别,就是公式左边的x变成差分算子,保证数据的稳定性。
差分算子就是:
令 wt 为:
则 ARIMA 就可以写成:
ARIMA模型运用的基本流程有几下几步:
- 数据可视化,识别平稳性。
- 对非平稳的时间序列数据,做差分,得到平稳序列。
- 建立合适的模型。
平稳化处理后,若偏自相关函数是截尾的,而自相关函数是拖尾的,则建立AR模型;
若偏自相关函数是拖尾的,而自相关函数是截尾的,则建立MA模型;
若偏自相关函数和自相关函数均是拖尾的,则序列适合ARMA模型。 - 模型的阶数在确定之后,对ARMA模型进行参数估计,比较常用是最小二乘法进行参数估计。
- 假设检验,判断(诊断)残差序列是否为白噪声序列。
- 利用已通过检验的模型进行预测。
HoltWinters 指数平滑时序预测模型
1、移动平均(The simple moving average (SMA))
直观上,最简单的平滑时间序列的方法,是实现一个无权重的移动平均。目前已知的方法是用窗口函数,平滑统计量 St 就是最近k个观察值的均值。公式如下: ![]()
这种方法存在明显的缺陷:当 k 较小时,预测的数据平滑效果不明显,而且突出反映了数据最近的变化;当 k 较大时,虽然有较好的平滑效果,但是预测的数据存在延迟。而且最少需要k个值(窗口有限)。【所以,通过历史数据观测,发现时序预测的数据规律,极大相似最近的数据规律时,就可以考虑,到HoltWinters源码中的指定方法,调参 k 值。】
2、加权移动平均
一种稍微复杂的方法是先选择一组权重因子来计算加权移动平均 ![]()
然后用这些权重来计算这些平滑统计量: ![]()
工程上,通常在选择权重因子时,赋予时间序列中的最新数据更大的权重,并减少对旧数据的权重。这个方法也需要最少 k 个值,并且计算复杂。
3、指数平滑法
移动平均模型,在解决时间序列问题上简单有效,但计算比较难。因为不能通过之前的计算结果推算出加权移动平均值。此外,移动平均法不能很好的处理数据集边缘的数据变化,也不能应用于现有数据集的范围之外。因此,移动平均法的预测效果相对较差。
指数平滑法(exponential smoothing)是一种简单的计算方案,可以有效的避免上述问题。按照模型参数的不同,指数平滑的形式分为:一次指数平滑法,针对没有趋势和季节性的序列;二次指数平滑法,针对有趋势但是没有季节特性的时间序列;
三次指数平滑法(术语“Holt-Winter”指的就是三次指数平滑),可以预测具有趋势和季节性的时间序列。Holt-Winter指数平滑法,按照季节性分量的计算方式不同,分为累加式季节性分量和累乘式季节性分量。两种不同的分量对应的时间序列计算等式和预测公式均不同。
所有的指数平滑法,都要更新上一时间步长的计算结果,并使用当前时间步长的数据中包含的新信息。它们通过“混合”新信息和旧信息来实现,而相关的新旧信息的权重由一个可调整的拌和参数来控制。各种方法的不同之处在于它们跟踪的量的个数和对应的拌和参数的个数。三次指数平滑法,功能最强大,既能体现趋势性又能体现季节性,所以三次指数平滑法的参数最多,有三个。
4、一次指数平滑法
指数平滑法是一种结合当前信息和过去信息的方法,新旧信息的权重由一个可调整的参数控制,各种变形的区别之处在于其“混合”的过去信息量的多少和参数的个数。
常见的有单指数平滑、双指数平滑。它们都只有一个加权因子,但是双指数平滑使用相同的参数将但指数平滑进行两次,适用于有线性趋势的序列。单指数平滑实质上就是自适应预期模型,适用于序列值在一个常数均值上下随机波动的情况,无趋势及季节要素的情况,单指数平滑的预测对所有未来的观测值都是常数。
幸运地是有一种方法可以避免上述问题,它叫做指数平滑法。 一次指数平滑,也称为简单指数平滑法,递推关系公式:
![]()
其中 α 是平滑因子,0 < α < 1。换句话说,平滑统计值 St 是当前统计值 Xt 与上一时间平滑值 St-1 的加权平均。这个简单指数平滑是很容易被应用的,因为只要有两个观察值就能计算了。
其中,s_i是第i步经过平滑的值,x_i是这个时间的实际数据。alpha是加权因子,取值范围为[0,1],它控制着新旧信息之间的权重平衡。当alpha接近1时,我们就只保留当前数据点(即完全没有对序列做平滑操作),当alpha接近0时,我们只保留前面的平滑值,整个曲线是一条水平的直线。在该方法中,越早的平滑值作用越小,从这个角度看,指数平滑法像拥有无限记忆且权值呈指数级递减的移动平均法。
这里 α 的选取,可以采用最小二乘来决定 α 。(最小化 ![]() )
)
一次指数平滑法的预测公式为:![]()
因此,一次指数平滑法得到的预测结果在任何时候都是一条直线。并不适合于具有总体趋势的时间序列,如果用来处理有总体趋势的序列,平滑值将滞后于原始数据,除非alpha的值非常接近1,但这样使得序列不够平滑。
为什么被称为“指数”平滑法 ?
从它的递推公式就能发现: 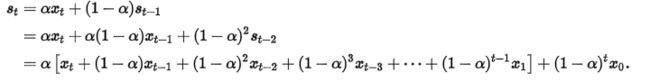
简单指数平滑法,适用于没有总体趋势的时间序列。如果用来处理有总体趋势的序列,平滑值将往往滞后于原始数据,除非 α 的值接近1,但这样一来就会造成不够平滑。【所以,此处需要慎重考虑,也要由场景决定。】
4、二次指数平滑法
为解决上述问题,引出二次指数平滑,能够保留总体趋势信息。因为将指数平滑应用了两次,所以被称为二次指数平滑。与简单指数平滑相比,二次指数平滑加入了时间趋势统计量 bt,公式如下: ![]()
若要预测 Xt 后 m 天,公式如下: ![]()
二次指数平滑法保留了平滑信息和趋势信息,使得模型可以预测具有趋势的时间序列。二次指数平滑法有两个等式和两个参数:
![]()
t_i代表平滑后的趋势,当前趋势的未平滑值是当前平滑值s_i和上一个平滑值s_{i-1}的差。s_i为当前平滑值,是在一次指数平滑基础上加入了上一步的趋势信息t_{i-1}。利用这种方法做预测,就取最后的平滑值,然后每增加一个时间步长,就在该平滑值上增加一个t_{i}:
![]()
在计算的形式上这种方法与三次指数平滑法类似,因此,二次指数平滑法也被称为无季节性的Holt-Winter平滑法。
5、三次指数平滑法
三次指数平滑(Holt-Winters模型)相比二次指数平滑,增加了第三个量来描述季节性。即将时间序列的季节性这一特征也考虑进去了。
季节性被定义为时间序列数据的趋势,它表现出每一个周期重复自身的行为,就像任何周期函数一样。“季节”这个词用来表示行为每隔时间段 L 就开始重复。在自然界中有不同类型的季节性“累加性”(additive)和“累乘性“(multiplicative),就像加法和乘法是数学的基本运算。
HoltWinters github 源码:https://github.com/sryza/spark-timeseries/blob/master/src/main/scala/com/cloudera/sparkts/models/HoltWinters.scala
如果每个12月都比每个11月多卖出1000套公寓,这样的季节趋势是“累加性”的。可以用绝对增长来表示。如果在夏季比冬季多卖出10%的公寓,那么季节趋势在自然中是“累乘性”的。
累乘性公式如下: ![]()
其中 α 是数据平滑因子 0 < α < 1;β是趋势平滑因子 0 < β < 1; γ是季节改变平滑因子 0 < γ < 1。
初始化趋势估计b0的公式为: ![]()
累加性公式如下: ![]()
对于三次指数平滑法,必须初始化一个完整的“季节”Ci的值,或可以简单地设置为全1(针对累乘式)或全0(针对累加式)。只有当序列的长度较短时,才需要慎重考虑初始值的选取。
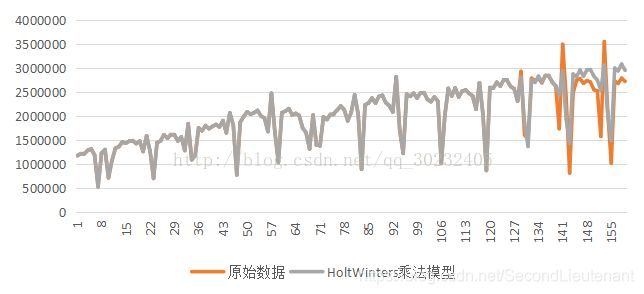
建立Arima或者HoltWinters模型预测
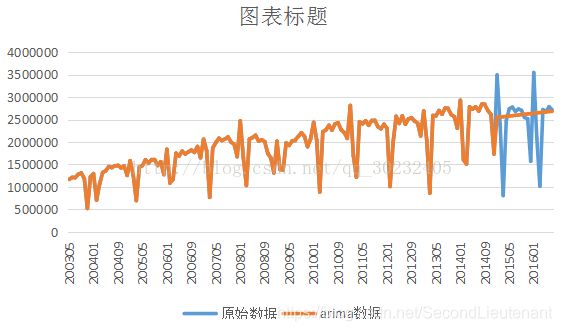
Arima的预测图:
从这两个图形上可以看出来,Arima模型没有针对实际的季节性部分来进行预测,所以预测效果比HoltWinters要差。
时序预测模型 效果评估
1. 效果评估
设 y 是时间序列的真实值, yhat 是模型的预测值。在分类模型中由于y是离散的,有很多维度可以去刻画预测的效果。但现在的y是连续的,需要关注的少了很多,省去了特征工程。
时间序列里比较常用的是 误差率 MAPE(mean absolute percentage error) 和 RMSE (root mean square error)
误差率 MAPE 比较实用,适合汇报,它揭示了预测值在真实值基础上的波动范围。比如,MAPE=10%,其代表着预测值的范围大致是 0.9y 至 1.1y 。
这两个指标或多或少都会有一些缺点,因此也有了各种变体,比如 SMAPE, NRMSE 等,感兴趣的可以自己去Wiki看看。
2. 交叉验证
因为时间序列的样本之间是无法交换的,所以没办法随机的像 KFold 一样把数据集切分成若干份训练集和测试集。但没关系,方法还是有的。
一个比较好的思路是按照时间顺序设置 cutoff time T_c :
这里有三个参数:
-
horizon: 模型预测的范围,如从cutoff点开始数未来30天
-
period: 每两个 cutoff 点之间的间隔,如60天
-
initial: 用于训练的日期范围,如730天
假设我们有2015-01-01 至 2017-12-31 共三年的数据。且三个参数的值如下: horizon=30,period=120,initial=730,则我们有
5组训练集和测试集。
有了交叉验证,就能获得评估模型效果和进行超参数优化了.
附:时序预测的七种方法
方法 1 –以Naive简单、朴素的方式开始
方法2 – 简单平均数
方法3 – 移动平均数
方法 4 –指数平滑法
方法5 – Holt线性趋势法
方法6 – Holt冬季季节法
方法7 –综合自回归移动平均法(ARIMA)
作者:阿里云云栖社区
链接:https://www.jianshu.com/p/3afbb01c9ed6
预测不是衡量准确性,而是偏差率
需求预测就如发射导弹,一路飞去,一路纠偏。命准目标的过程其实就是纠正偏差的过程。
预测就如赌博,赌对说明了什么?说明了你幸运。我们其实是很难分析赌对的原因,除了基本的“从数据出发,由判断结束”的需求预测流程,以及选择更合适的数理统计模型。即使这两者都做对了,你还是可能预测失败。所以,从赌对中,我们很难学到太多的东西。这就如你问那位九十多岁的老寿星长寿的秘诀,他说他吃饭,他运动,他睡觉--他其实也不知道为什么长寿,否则的话,为什么不教给他的老伴儿,这样,老伴儿就不会在三十年前去世了。
成功并不能让我们更聪明多少,也很难复制。否则的话,马云会把他的那些成功法则一遍又一遍地复制,把地球上的钱都赚光了;苹果也是,把iPhone的成功复制到i汽车、i电视、i电冰箱,凡是你能想到的,前面都加个i。人之所以变聪明,是因为我们从失败中学习。具体地说,就是坚守基本原则的情况下,尽量避免那些失败,这样就增加成功的概率。
就拿长寿来说,基本原则就是吃好、运动好、休息好。要避免的失败呢,就是不吸毒,少喝酒,不在XYZ公司上班--加班太多,过劳死;压力太大,容易跳楼。对于需求预测来说,坚持基本原则就是选择最合适的统计模型,走"从数据出发,由判断结束"的基本流程。而要避免的失败呢,则得从预测的偏差率中去发现--所有的预测都是错的,识别偏差,纠正差别就是调整预测的过程。
需求预测就如发射导弹,一路飞去,一路纠偏。命准目标的过程其实就是纠正偏差的过程。
图1 导弹击中目标的过程,就是发现偏差,纠正偏差的过程
让我们先来看偏差怎么计算。概念上很简单:实际值与预测值的差就是偏差。但预测是个循环更新的过程,如果每月滚动的话,每一个月就有个预测。那究竟该用哪个月的预测来计算偏差?这取决于供应链的响应周期:在一般的行业,生产周期加上长周期物料的采购前置期,大概在3个月左右。因此,理论上讲,用三个月前的预测(M-3)最合理:1月份,你告诉我4月份的预测是100个,我就按照这个来采购、生产。结果4月份的实际需求是80个,那么偏差就是20个,偏差率是25%。
M-3的偏差率一般会非常高,会揭示太多的"问题"。而最大的问题呢,就是预测做得太早而不准,解决方案就是缩短供应链的响应周期,这样我们就不需要那么早地做预测了。所以时间是最大的因素,对于需求预测来说又不可控,反倒把很多别的可控因素给掩盖了。
打个不一定很恰当的比方。乔丹的投篮命准率是49.7%,这是他在三分线内外的命准率。假定乔丹一过中场就投篮,估计命准率只有5%。分析为什么95%的球都投丢了,结论很容易是他离篮板太远了。其实即使乔丹在篮下,跟篮板的距离是0,也不是百分之百地命准。这意味着在距离因素以外,还有别的因素在影响他的投篮命准率,比如投篮的姿势,手腕的发力等。这些其实是可以控制的,但因为被距离因素掩盖掉了,反倒没有被发现,采取合适的纠偏措施。
有些企业用M-1来统计偏差,用1个月前的预测作为基准。这有一定的合理性,因为一般的行业,需求预测的冻结期大概是1个月以内(意味着数量、配置和日期都不能改变),如果进入冻结期还改变预测,那对生产和供应链的代价很高,所以必须严加控制。半冻结期大概在1到2个月,这段时间内的需求变化呢,对不起,供应链你就想法消化吧。就这样,冻结期内的问题由销售买单;半冻结区内的变动由供应链买单,两头一凑,算是个折中方案吧。
但是,对于芯片等采购提前期很长(动辄就13个星期或更长),供应灵活性很差的情况(比如芯片生产流程很长很复杂,人工干预挺困难),M-1对供应链来说就有点太不公平--M-1的预测准确度挺高,但太迟了,因为供应链的决策早都做了。这就是为什么有些企业用M-2来统计预测的准确度,分析其偏差度。当然,还有些企业采取更折中的方式,用M-1、M-2、M-3的平均值来统计需求预测的差异,这在操作上有点太复杂,也掩盖了不少有用的信息,指导意义有多大,还有待商榷。
其实,采用多久前的预测做基准,其实是销售与供应链力量博弈的结果:销售的力量越强,就选择近期的预测做基准;供应链的胳膊越粗,就越可能用更久前的预测做基准。想必我们现在也清楚了,如果两家公司都说他们的预测偏差是30%时,如果一个用的是M-1,另一个是M-3,那他们的差距可不是一点点喔。
定义好了偏差怎么计算,让我们进一步探讨差异是怎么分析的。总的来说,我们感兴趣有几个方面:绝对偏差(绝对值),相对偏差(百分比),偏差的方向(偏见)。
先说绝对偏差。假定需求预测是100,实际需求是80,那么绝对偏差就是20。除以实际需求80,就得到绝对百分比偏差25%。绝对百分比让不同的产品有了可比性,所以是差异分析中较常用的一种。不过你看得出,绝对百分比掩盖了偏差方向,没法判断预测是虚高还是虚低。比如需求预测是60,实际需求是80,其百分比差异也是25%。但你知道,这是预测虚低,会造成短缺,跟预测100、实际80造成的过剩不一样,对供应链的影响也不同。
这就是为什么有些公司拿掉绝对值,直接计算预测和实际的偏差百分比。这种偏差可以清楚地判断预测与实际的偏差方向,以揭示需求预测中的系统性偏见。比如"由判断结束"中,有几个销售人员习惯性地高估需求,而别的销售人员时高时低,更加符合统计学规律。根据这样的分析,就可有针对性地采取组织措施,纠正这几个销售人员的行为。
有的公司把预测和实际的偏差值累计起来,就得到累计偏差,以判断预测的累计影响。比如而1月、2月、3月的预测偏高,4月、5月、6月的偏低,半年加起来可能抵消,从而没有造成呆滞库存。不过这并不意味着完美无缺。比如基于前三个月的过高预测,供应链可能不得不赶工加急,造成额外的运营成本;由于后三个月的预测偏低,工厂可能遣散一部分员工,产生遣散费用。可以说,一旦汇总,我们可能冒丧失某些信息、掩盖某些问题的风险。所以,预测的累计偏差一般不独立使用,而是和别的偏差指标一起用。
此外,还有很多偏差的统计方法,比如统计预测值与实际值之间的方差、均方差,来衡量偏差的幅度和离散度。但不管用什么样的统计方法,超过一定限度的会成为异常值,需要根源分析,采取纠偏措施。需求预测虽说是"预测",其实大部分时间都在纠偏:发现差异,分析差异,理解差异,采取纠偏措施,比如更换统计模型,与销售、市场、产品管理会面讨论,和关联职能协商等。正是通过处理一个个的“例外”,我们才得以避免失败,从而能够成功。这就如要长寿很简单,只要解决那些可能让你死去的“例外”,活着就是长寿。
转载:http://articles.e-works.net.cn/scm/article140914.htm