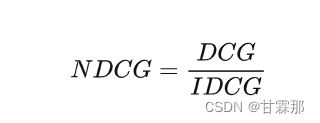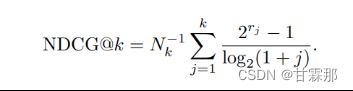推荐系统笔记(三):NDCG Loss原理及其实现
背景
NDCG的全称是:Normalized Discounted Cumulative Gain(归一化折损累计增益),和他的字面意思一样,为了评估一个序列排序的好坏,设计了排序的损失,这就是CG方法,即Cumulative Gain: 表示对K个item的Gain进行累加。CG只是单纯累加相关性,不考虑位置信息。
但是排在不同位置的损失应该是不一样的,如第一个排错和最后几个排错他们的错误代价应该是不等的,list中item的顺序很重要,不同位置的贡献不同,一般来说,排在前面的item影响更大,排在后面的item影响较小。因此需要设计一个带折扣的损失函数,这就是DCG折扣累计。即Discounted Cumulative Gain: 考虑排序顺序的因素,使得排名靠前的item增益更高,对排名靠后的item进行折损。
但是排序列表长度不一样会对结果造成很大的影响,如对浏览器检索的推荐顺序,输入不同关键词推荐出的页面总数可能有很大差别,这会造成页面多的DCG会更大,因而无法对推荐算法进行比较,因此归一化是必要的,因此设计了NDCG。
思想
CG只是单纯累加相关性,不考虑位置信息。而DCG没有考虑到推荐列表和每个检索中真正有效结果个数,所以最后我们引入NDCG(normalized discounted CG),顾名思义就是标准化之后的DCG。
NDCG参考论文:A General Approximation Framework for Direct Optimization of Information Retrieval Measures
视频讲解链接:l2r-dcg&ndcg_哔哩哔哩_bilibili
原理和计算
1.NDCG 增益函数:
(1)传统方法,一般是用在推荐系统中的,是带有折扣(距离越远折扣越大)和归一化的增益函数。
计算步骤及举例:
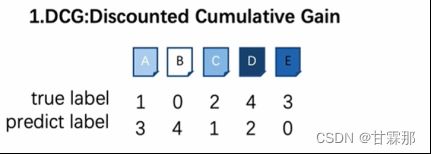
1.首先,有五个搜索文件A、B、C、D、E,按照重要程度进行排序,有真实的标签排序和预测的标签0-4进行排序,分别如图为10243、34120,比如B的概率最大,我们就把他排在第0位。
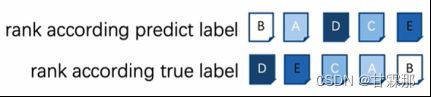
2.然后,按照标签由小到大的顺序对信息进行排序,就类似于百度搜索关键词一样,把最相近的放在前边。
3.接着,按照公式计算DCG和IDCG,DCG是预测的增益折扣计算累计,IDCG是真实标签,即ideal排序的增益累计。
DCG计算为:
IDCG计算为:
我们可以发现,计算的分母的j是按照12345排列的,代表的是一个折扣的递增,越远的信息,折扣越大,分母就是折扣。
而DCG分子2的指数的幂依次对应的是II中的”rank according predict label”的排列对应的I中的true label标签数字,比如II中排在第一个的是B,而B之前的标签是0,因此DCG的第一个分子为2^0-1,以此类推。
IDCG的分子是因为我们就是按照真实地去对IDCG对应的标签排序,其的分子分别为2^4-1,2^3-1,2^2-1...2^0-1。
NDCG等于:
优点:越相关的其越被重视;实现了使用相关性做梯度下降。
延伸与拓展
NDCG经过处理也可以作为损失函数使用,而不仅仅作为评估指标。具体请参考论文:
Learning Relaxed Belady for Content Distribution Network Caching
实现
其中pred_matrix和truth_matrix分别嗲表预测和真实的结果的序列矩阵。
pred_matrix = np.array(pred_matrix)
idcg = np.sum(truth_matrix*(1/np.log(np.arange(2,k+2))), axis = 1)
dcg = np.sum(pred_matrix*(1/np.log(np.arange(2,k+2))), axis = 1)
idcg[idcg == 0] = 1
ndcg = dcg/idcg
eval_score += np.sum(ndcg)总结
为了做一个归一化数据,我们在检索的时候,可能返回的数据有很多条,累加的数目不一样,无法对两个搜索模型进行比较,就行在缓存中,当缓存行分别有10条和20条,他们的DCG之和不具有可比性,需要归一化才能定性的比较,这就是NDCG的主要思想。
参考视频链接:l2r-dcg&ndcg_哔哩哔哩_bilibili