【数据结构】认清带头双向循环链表的庐山真面目

前言

前面我们学习的是单链表，我们主要学习的是不带头结点的单链表，这个单链表是单向的，只支持从前往后遍历，也就是说它只能从上一个结点找到下一个结点，不能从下一个结点找到上一个结点，因此在解决一些问题的时候就会比较麻烦。今天我们将学习一个比较优秀的链表：带头双向循环链表

一、带头双向循环链表的介绍

1. 基本样式
   
2. 结构分析

• 带头：结构中具有头结点，就是在插入的时候不需要对插入第一个结点进行特殊处理，这是相比于不带头结点的优势
• 双向：支持从上一个结点找到下一个结点，也支持从下一个结点找到上一个结点，支持双向遍历
• 循环：尾结点指向的是头结点，头结点的前一个指向的是尾结点，因此在找尾的时候就会比较方便

二、带头双向循环链表的类型重定义

1.对数据类型进行重定义

与前面学习的数据结构一样，数据结构都是用来存储数据的，存储的数据类型是未知的，因此，我们最好对数据类型进行重定义，以便后面随时可以修改存储的数据类型，这里先假设存储的是int类型，如果我们想要将存储的数据类型修改成double,那么我们只需要修改这里的int为double即可。

// 对结构中存储的数据类型进行重定义
typedef int ListDataType;

2.链表结点结构

我们知道带头双向循环链表中是支持双向遍历的，也就是支持从上一个结点找到下一个结点，支持从下一个结点找到上一个结点，这些都是由链表中的结点的结构来决定的。链表中的结点的结构中除了需要包含存储的数据之外，还需要一个指向前一个结点的指针和一个指向后一个结点的指针，这样才能满足上面的需求。大致实现如下：

// 链表中的结点类型
struct ListNode
{
	ListDataType val;// 数据域
	struct ListNode* prev;// 指向前一个结点的指针
	struct ListNode* next;// 指向下一个结点的指针
};

3.结点类型重定义

通常为了方便表示结点的类型，也就是为了每次使用结点类型的时候不加struct这个关键字或者更加简短，通常会对结点的类型进行重定义成一个更简短的名字。比如：

// 链表中的结点类型
typedef struct ListNode
{
	ListDataType val;// 数据域
	struct ListNode* prev;// 指向前一个结点的指针
	struct ListNode* next;// 指向下一个结点的指针
}ListNode;

三、常见函数操作的实现

1.声明

// 实现带头双向循环链表中的常见的操作
// 申请新节点
ListNode* BuyListNode(ListDataType val);
// 初始化
ListNode* ListInit();

// 销毁链表
void ListDestroy(ListNode* head);

// 尾插数据
void ListPushBack(ListNode* head, ListDataType val);

// 尾删数据
void ListPopBack(ListNode* head);

// 头插数据
void ListPushFront(ListNode* head, ListDataType val);

// 头删数据
void ListPopFront(ListNode* head);

// 在指定的位置插入数据
void ListInsert(ListNode* head, ListNode* pos, ListDataType val);

// 在指定位置删除数据
void ListErase(ListNode* head, ListNode* pos);

// 链表中的结点个数
int ListSize(ListNode* head);

// 打印链表
void ListPrint(ListNode* head);

// 根据指定值找结点
ListNode* ListFind(ListNode* head, ListDataType val);

2.定义

1. 申请新节点

// 申请新节点
ListNode* BuyListNode(ListDataType val)
{
	ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		return;
	}
	// malloc success
	newnode->val = val;
	newnode->next = NULL;
	return newnode;
}

由于在链表中的各种插入中需要频繁使用申请新节点这个功能，为了防止程序中代码冗余，我们可以将申请新节点这个功能封装成一个新的函数，这个函数中需要注意一些点，就是指针问题，当一个结点成功创建之后一定要注意马上对其中的指针进行处理，防止后续出现野指针

2. 初始化

// 初始化
ListNode* ListInit()
{
	ListNode* head = BuyListNode(0);
	head->next = head;
	head->prev = head;
	return head;
}

初始化函数主要是为了完成头结点中指针的初始化，防止出现野指针，当带头双向循环链表为空时，头结点中的prev指针和next指针都是指向本身，结点中的数据域可初始化可不初始化，不初始化时就默认是随机值，不影响。这个初始化函数是通过在初始化函数中初始化链表的头结点之后返回对应的头指针来实现的，而不是将头指针交给初始化函数进行初始化，这个细节是需要注意的

3. 销毁链表

// 销毁链表
void ListDestroy(ListNode* head)
{
	assert(head);
	// 从第一个结点（非头结点）开始进行释放结点
	ListNode* cur = head->next;
	while (cur != head)
	{
		ListNode* next = cur->next;
		free(cur);
		cur = next;
	}
	head->next = head->prev = head;
}

带头双向循环链表的销毁和单链表的销毁思路基本一致，需要一个遍历指针从第一个有效结点开始，不断释放结点，直到再次遍历到头结点时停止。释放有效结点之后需要将head结点的prev指针和next指针指向其本身。

4. 打印链表

// 打印链表
void ListPrint(ListNode* head)
{
	assert(head);
	ListNode* cur = head->next;
	while (cur != head)
	{
		printf("%d ", cur->val);
		cur = cur->next;
	}
}

思路和单链表类似

5. 尾插数据

// 尾插数据
void ListPushBack(ListNode* head, ListDataType val)
{
	assert(head);
	ListNode* newnode = BuyListNode(val);
	// 找尾
	ListNode* tail = head->prev;

	// 连接
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = head;
	head->prev = newnode;
	
}

尾插数据的时候不需要像单链表一样去从头遍历找尾，尾结点就是头结点的前一个，找到尾结点之后，再将新节点连接到尾结点和头结点之间即可。

6. 尾删数据

// 尾删数据
void ListPopBack(ListNode* head)
{
	assert(head);
	assert(head->next);
	// 找尾
	ListNode* tail = head->prev;
	// 找尾的前一个
	ListNode* Tailprev = tail->prev;
	// 释放尾结点
	free(tail);
	// 连接尾结点的前后结点
	Tailprev->next = head;
	head->prev = Tailprev;
}

找到尾，尾的前一个，删除尾结点，连接尾结点的前后结点，删除的算法一定要注意，删除的结构是否为空，如果结构中就没有数据，那么是不能删除的。

7. 头插结点

// 头插数据
void ListPushFront(ListNode* head, ListDataType val)
{
	assert(head);
	// 申请新节点
	ListNode* newnode = BuyListNode(val);
	// 找到头结点的下一个结点
	ListNode* next = head->next;

	// 头插数据
	head->next = newnode;
	newnode->prev = head;
	newnode->next = next;
	next->prev = newnode;

}

先找到第一个结点，申请一个新节点，将新节点连接在头结点和原来第一个结点之间即可

8.头删结点

// 头删数据
void ListPopFront(ListNode* head)
{
	assert(head);
	assert(head->next);
	// 找到第一个有效结点
	ListNode* cur = head->next;
	// 找到第一个有效结点的下一个结点
	ListNode* next = cur->next;
	// 删除第一个有效结点
	free(cur);
	// 连接第一个有效结点的前后结点
	head->next = next;
	next->prev = head;
}

先找到第一个结点（要删除的结点）的下一个位置（可能为空），删除第一个结点，再让头结点指向刚刚找到的第一个结点的下一个位置。

9. 在指定的位置前插入数据

// 在指定的位置插入数据
void ListInsert(ListNode* head, ListNode* pos, ListDataType val)
{
	assert(head);
	// 申请新节点
	ListNode* newnode = BuyListNode(val);
	// 在pos位置前插入数据
	// 找到pos位置结点的前一个结点
	ListNode* prev = pos->prev;
	prev->next = newnode;
	newnode->prev = prev;

	newnode->next = pos;
	pos->prev = newnode;

}

上面这个代码实现的是在指定位置前插入数据，当然也可以实现一个在指定位置后插入数据，这个可以根据需求来实现，基本逻辑，找到指定位置的前一个结点，申请一个新节点，将指定位置的前一个结点的下一个连接为新节点，将新节点的下一个结点连接为指定的那个结点即可。

10. 在指定位置删除数据

// 在指定位置删除数据
void ListErase(ListNode* head, ListNode* pos)
{
	assert(head);
	assert(head->next);

	// 找到pos位置的前一个结点
	ListNode* prev = pos->prev;

	// 找到pos位置的下一个结点
	ListNode* next = pos->next;

	// 删除pos位置的结点
	free(pos);
	prev->next = next;
	next->prev = prev;
}

给定了某个结点的地址，在双向循环链表中我们可以通过这个结点的指针找到这个结点的前一个结点和后一个结点，那么现在需要删除这个结点，我们只需要删除这个结点之后，将这个结点的前后指针连接起来即可。

11. 链表中的结点个数

// 链表中的结点个数
int ListSize(ListNode* head)
{
	int count = 0;
	ListNode* cur = head->next;
	while (cur != head)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

12. 根据指定值找结点

// 根据指定值找结点
ListNode* ListFind(ListNode* head, ListDataType val)
{
	assert(head);
	ListNode* cur = head->next;
	while (cur != head)
	{
		if (cur->val == val)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;
}

四、测试链表逻辑

1.尾插数据

• 测试代码

void test_list1()
{
	// 初始化
	ListNode* plist = ListInit();
	
	// 尾插数据
	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);

	// 打印链表
	ListPrint(plist);
}

• 测试结果：
  

2.尾删数据

• 测试代码

void test_list2()
{
	// 初始化
	ListNode* plist = ListInit();

	// 尾插数据
	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);

	// 打印链表
	ListPrint(plist);

	// 尾删数据
	ListPopBack(plist);
	// ListPopBack(plist);

	// 打印链表
	ListPrint(plist);
}

• 测试结果
  

3. 测试头插数据

• 测试代码

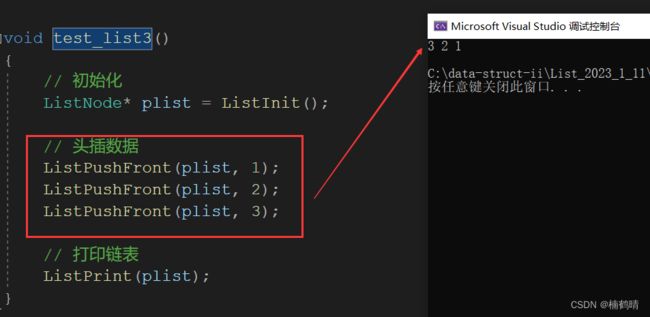
void test_list3()
{
	// 初始化
	ListNode* plist = ListInit();

	// 头插数据
	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);

	// 打印链表
	ListPrint(plist);
}

• 测试结果
  

4. 测试头删数据

• 测试代码

void test_list4()
{
	// 初始化
	ListNode* plist = ListInit();

	// 头插数据
	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);

	// 打印链表
	ListPrint(plist);

	// 头删数据
	ListPopFront(plist);
	ListPrint(plist);

	ListPopFront(plist);
	ListPrint(plist);

	ListPopFront(plist);
	ListPrint(plist);

	ListPopFront(plist);
	ListPrint(plist);

}

• 测试结果
  

5.测试在pos位置之前插入新节点

• 测试代码

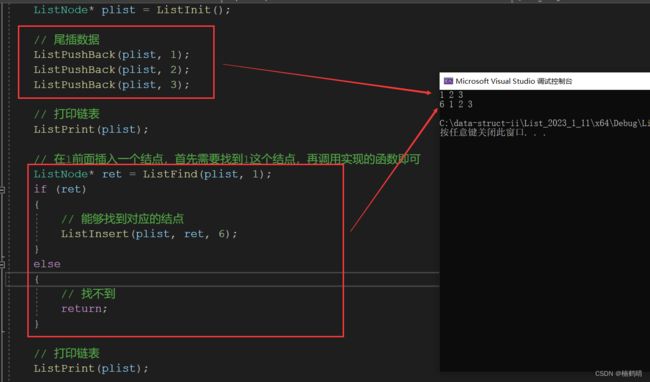
void test_list5()
{
	// 初始化
	ListNode* plist = ListInit();

	// 尾插数据
	ListPushBack(plist, 1);
	ListPushBack(plist, 2);
	ListPushBack(plist, 3);

	// 打印链表
	ListPrint(plist);

	// 在1前面插入一个结点，首先需要找到1这个结点，再调用实现的函数即可
	ListNode* ret = ListFind(plist, 1);
	if (ret)
	{
		// 能够找到对应的结点
		ListInsert(plist, ret, 6);
	}
	else
	{
		// 找不到
		return;
	}

	// 打印链表
	ListPrint(plist);

}

• 测试结果
  
• 测试逻辑
  先利用查找函数查找到对应的结点，如果查找不到，则啥事都不需要做，如果查找到，记录该节点，使用对应的函数进行插入数据即可

6.测试删除pos位置的结点

• 测试代码

void test_list6()
{
	// 调用erase函数删除3这个结点
	// 初始化
	ListNode* plist = ListInit();

	// 头插数据
	ListPushFront(plist, 1);
	ListPushFront(plist, 2);
	ListPushFront(plist, 3);

	// 打印链表
	ListPrint(plist);

	// 先找到3这个结点
	ListNode* ret = ListFind(plist,3);
	if (ret)
	{
		// 找到了
		ListErase(plist, ret);
	}
	else
	{
		// 找不到
		return;
	}

	// 打印链表
	ListPrint(plist);
}

• 测试结果
  

• 测试逻辑
  调用ListErase函数来删除某个指定的结点，通常的方法就是使用查找函数找到对应值的结点，然后将这个结点的指针传给ListErase函数进行删除即可。

---

通过上面的代码的测试已经实现，我们会发现，上面这个结构相比于之前学习的单链表拥有很大的优势，并且上面学习的这个结构相对是比较优秀的，那么上面这个结构有没有什么缺点呢？？
缺点通常都是相对而言的，正如：没有对比就没有伤害，相比于前面学习的顺序表，这个结构还是存在一定的缺点的，那么下面我们就来分析顺序表和带头双向循环链表的优缺点。

六、顺序表VS链表（面试常考）

1. 顺序表
   （1）优点：

• 物理空间连续，支持通过数组下标对数据进行随机访问
• CPU高速缓存命中率高
  （2）缺点
• 由于物理空间连续，当空间不够时就需要进行扩容，而扩容本身是具有一定的成本的，并且扩容也会存在一定的空间浪费，因为不可能刚好扩的空间是满足需求的
• 在顺序表的头部进行插入和删除的时候需要挪动大量的数据，效率比较低，成本比较高

2. 链表
   （1）优点

• 在任意的位置插入和删除数据的效率都比较高
• 可以按需申请对应的结点空间，并不会存在内存浪费
  （2）缺点
• 不支持通过下标进行随机访问
• 有些算法：二分查找，排序等不适合用在链表上

---

重点：如何理解顺序表的优点之CPU高速缓存命中率高？

七、顺序表的优点之CPU高速缓存命中率高

想要弄懂这个问题，首先需要知道一些背景知识：一个源代码在写好之后是
会通过编译链接形成一个可执行程序，这个时候这个可执行程序是存放在磁盘上的，当这个程序要被运行起来的时候，CPU会将这个程序从磁盘加载到内存，当CPU要去执行这个程序的时候，CPU是不会直接从内存拿数据的，因为CPU的执行速率比较快，而内存的运行速度相比于CPU而言还是比较慢的，所以CPU并不会直接从内存读数据，而是会将内存中需要运行的数据从内存中加载到高速缓存，所以CPU每次执行程序的时候都会去看看高速缓存中是否已经存在对应的数据和代码，如果存在，则称为CPU命中，若不存在，则称为不命中。当CPU第一次访问高速缓存的时候，显然这个时候不存在对应的数据，这个时候是不命中的，所以此时会将内存中对应的数据从内存加载到高速缓存，由局部性原理可知：一次加载并不仅仅是将要运行的数据加载进去，而是会将要运行的数据及其周围的数据一起加载到高速缓存。由于顺序表中数据是连续存放的，链表中的数据不是连续存放的，因此，在每次CPU进行命中的时候，显然使用顺序表时CPU的高速缓存命中率会比较高。